Autmatas finitos Tomado de Sudkamp Languages and Machines













- Slides: 33

Autómatas finitos Tomado de Sudkamp: Languages and Machines Cap. 6.

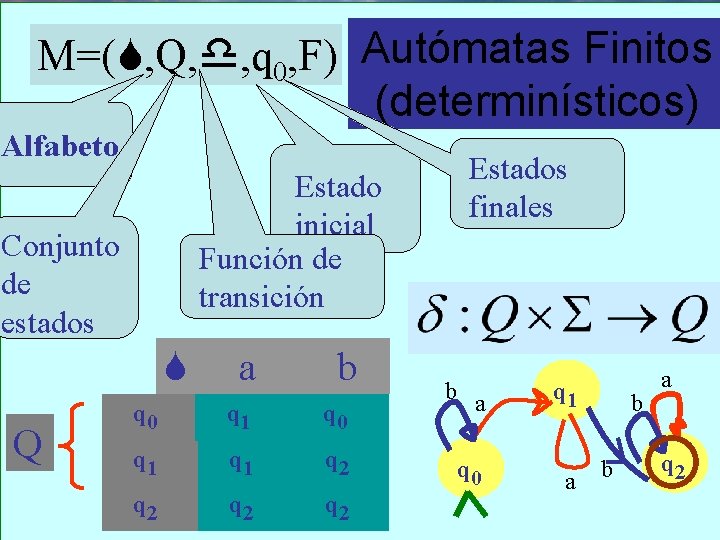
M=( , Q, , q 0, F) Autómatas Finitos (determinísticos) Alfabeto Estado inicial Función de transición Conjunto de estados Q a b q 0 q 1 q 1 q 2 q 2 Estados finales b a q 0 q 1 a b b a q 2

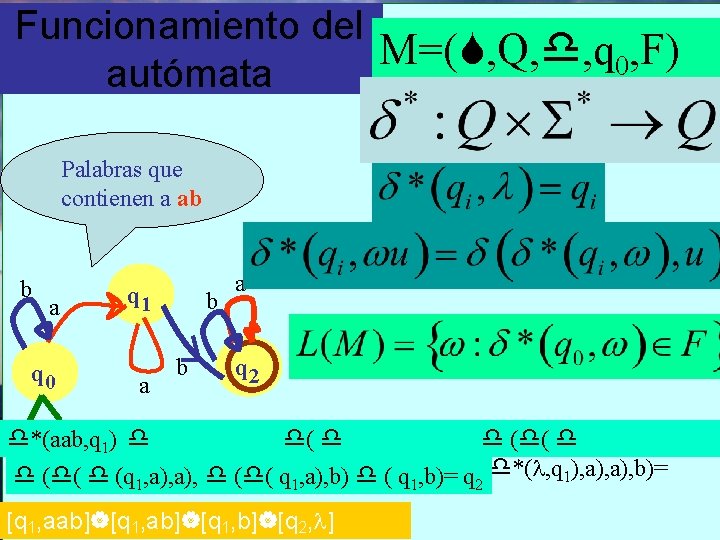
Funcionamiento del M=( , Q, , q 0, F) autómata Palabras que contienen a ab b a q 0 q 1 a b b a q 2 *(aab, q 1) ( ( ( = ( ( (q( *(aa, q 1), a), b)= 1), b)= ( ( q( *(a, q , a), b)= ( q , b)= q ( *( , q 1), a), b)= 1 1 [q 1, aab] [q 1, b] [q 2, ] 1 2

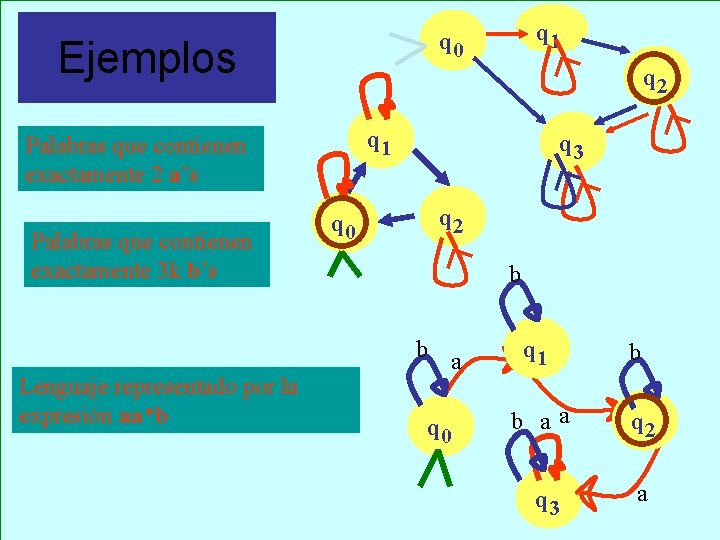
Ejemplos q 2 q 1 Palabras que contienen exactamente 2 a’s Palabras que contienen exactamente 3 k b’s Lenguaje representado por la expresión aa*b q 1 q 0 q 3 q 2 b b a q 0 q 1 b b aa q 2 q 3 a

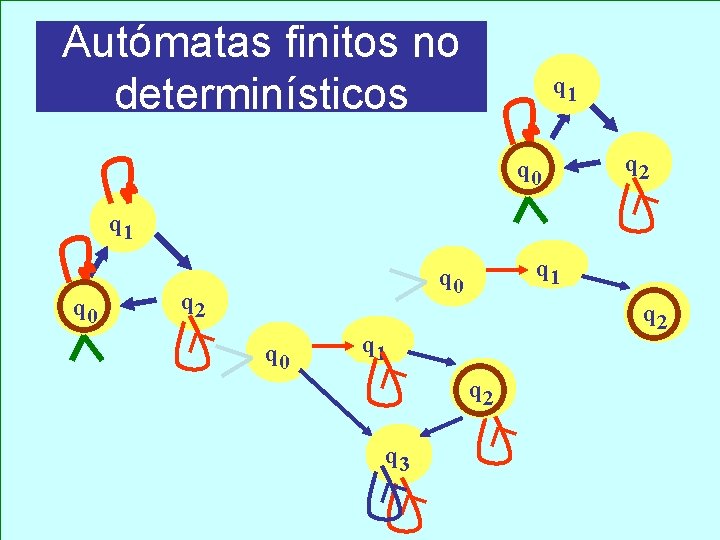
Autómatas finitos no determinísticos q 1 q 0 q 2 q 0 q 2 q 1 q 2 q 3

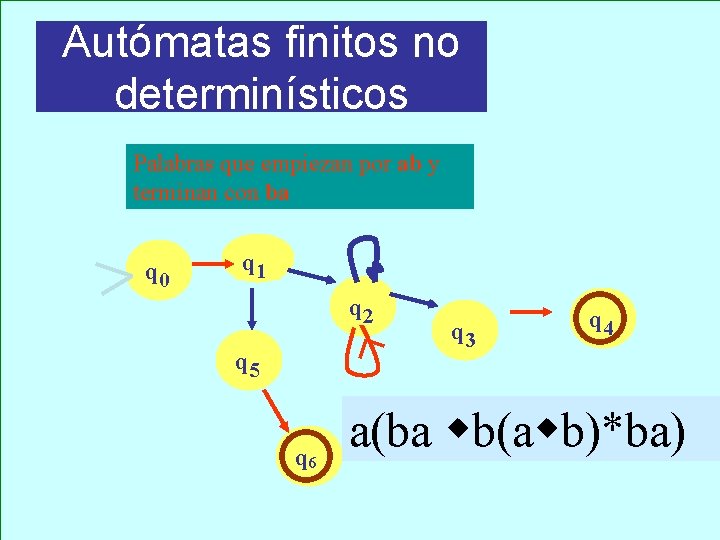
Autómatas finitos no determinísticos Palabras que empiezan por ab y terminan con ba q 0 q 1 q 2 q 5 q 6 q 3 q 4 a(ba b(a b)*ba)

Autómatas finitos no determinísticos M=( , Q, , q 0, F) q 1 q 0 q 2 q 0 q 4 q 3 q 1 q 2 q 3 q 4 a q 1 q 2 q 4 b q 2, q 3

Autómatas finitos no determinísticos M=( , Q, , q 0, F) qi w qk u qj

Autómatas FND M=( , Q, , q 0, F)

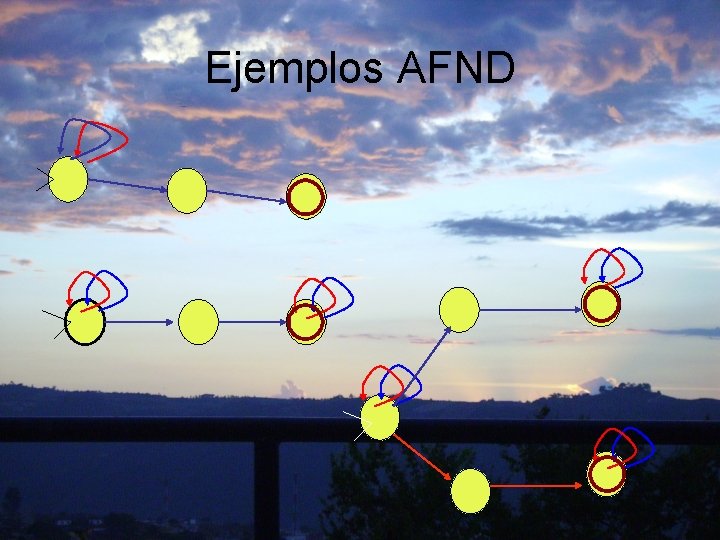
Ejemplos AFND

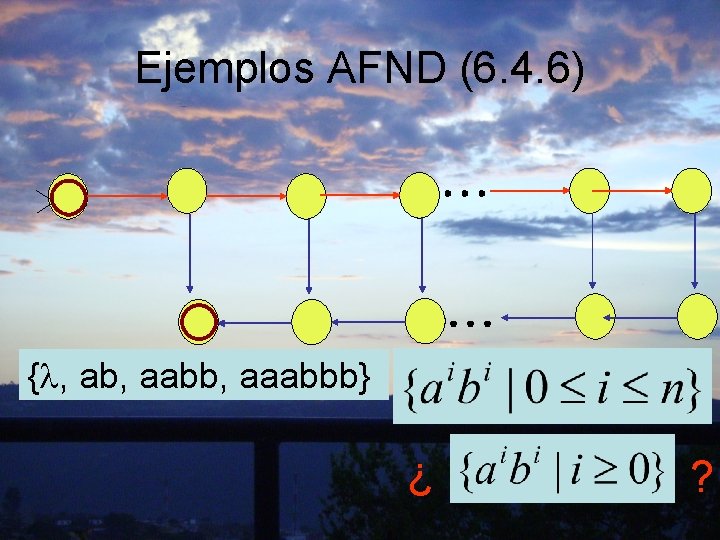
Ejemplos AFND (6. 4. 6) { , ab, aabb, aaabbb} ¿ ?

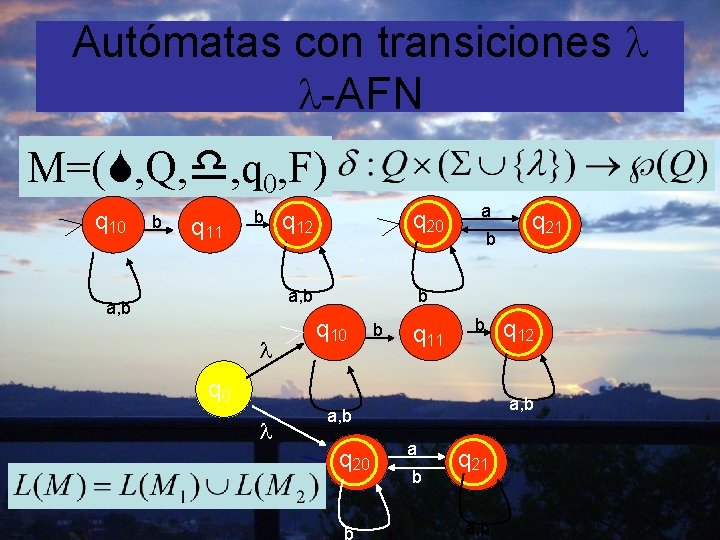
Autómatas con transiciones -AFN M=( , Q, , q 0, F) q 10 b q 11 b a, b q 12 q 20 a, b b q 10 b q 11 a b b q 0 q 12 a, b q 20 q 21 a b q 21 a, b

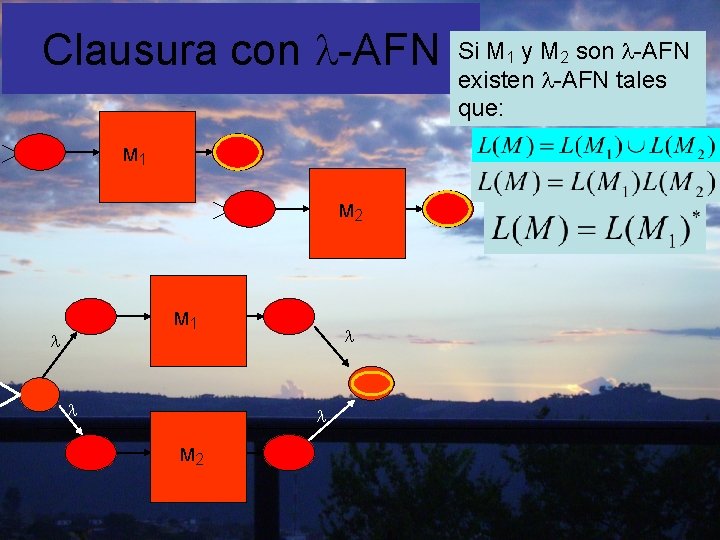
Clausura con -AFN M 1 M 2 M 1 M 2 Si M 1 y M 2 son -AFN existen -AFN tales que:

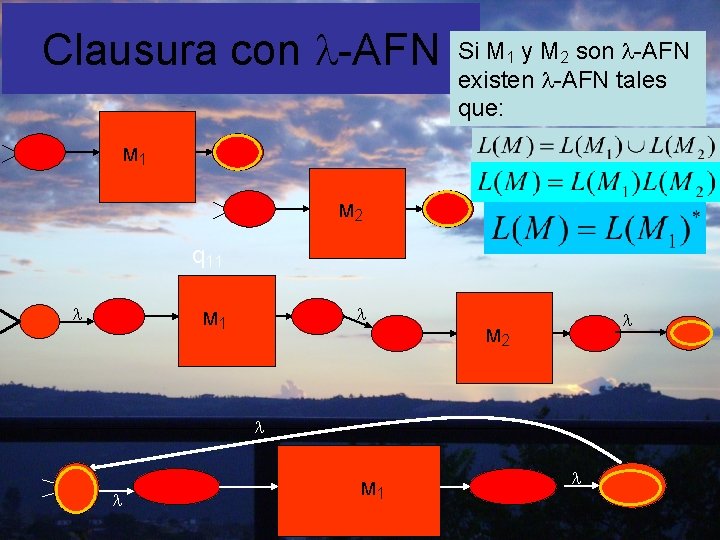
Clausura con -AFN Si M 1 y M 2 son -AFN existen -AFN tales que: M 1 M 2 q 11 M 1 M 2 M 1

Concluimos…. • Toda expresión regular tiene al menos un correspondiente -AFND que acepta exactamente las palabras correspondientes a la expresión.

Eliminando el indeterminismo La clausura Lambda, para cada estado qi, se construye recursivamente así: BASE: Paso recursivo La función de transición de entradas t para un -AFND se define así:

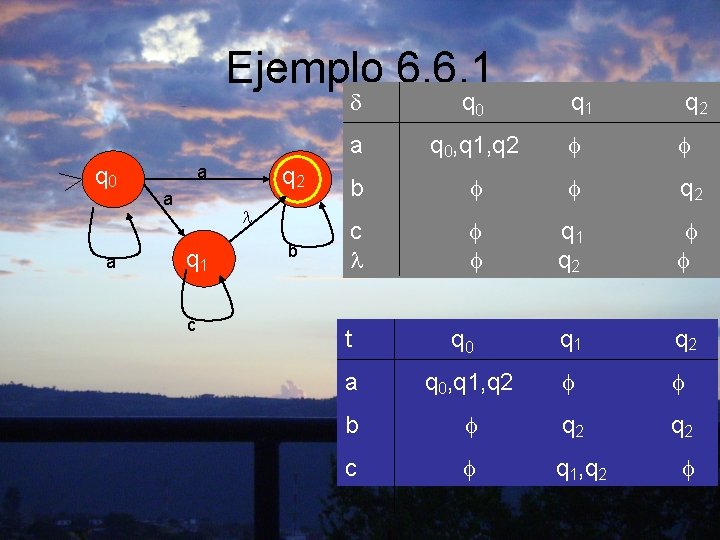
Ejemplo 6. 6. 1 q 0 a a a q 2 q 1 c b q 0 a q 0, q 1, q 2 b q 2 c q 1 q 2 t q 0 q 1 q 2 a q 0, q 1, q 2 b q 2 c q 1, q 2

Algoritmo 6. 6. 3 Construction of DM, a DFA Equivalent to NFA- M Input: an NFA- M=(Q, , , q 0, F). input transition fuction t of M 1. initialize Q’ to -Cl(q 0) 2. repeat 2. 1 if there is a node X Q’ and a symbol a with no arc leaving X labeled a then 2. 1. 1 let 2. 1. 2 if then set 2. 1. 3 add an arc from X to Y labeled a else done: =true until done 3. The set of accepting states of DM is F’={X Q’| X contiene algún elemento de F}

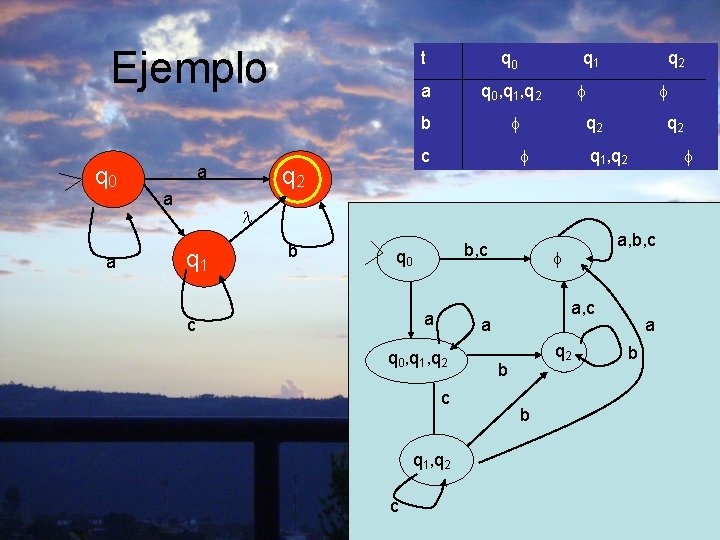
Ejemplo q 0 a a a t q 0 a q 0, q 1, q 2 b q 2 c q 2 q 1 q 2 q 1, q 2 q 1 b b, c q 0 a c c q 1, q 2 c a, c a q 0, q 1, q 2 a, b, c q 2 b b a b

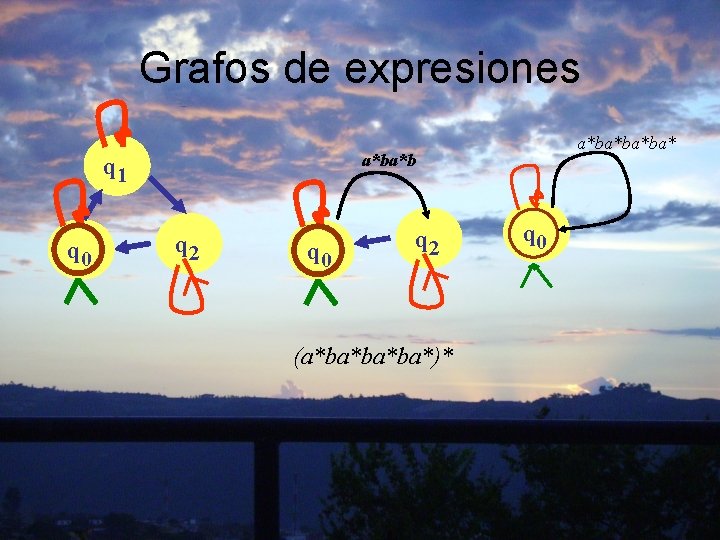
Grafos de expresiones a*ba*b q 1 q 0 a*ba*ba*ba* q 2 q 0 q 2 (a*ba*ba*ba*)* q 0

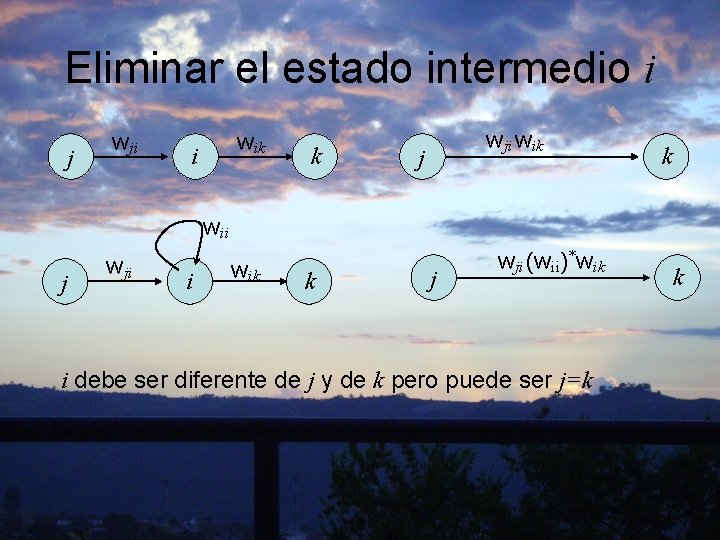
Eliminar el estado intermedio i j wji wik i k wji wik j k wii j wji i wik k j wji (wii)*wik i debe ser diferente de j y de k pero puede ser j=k k

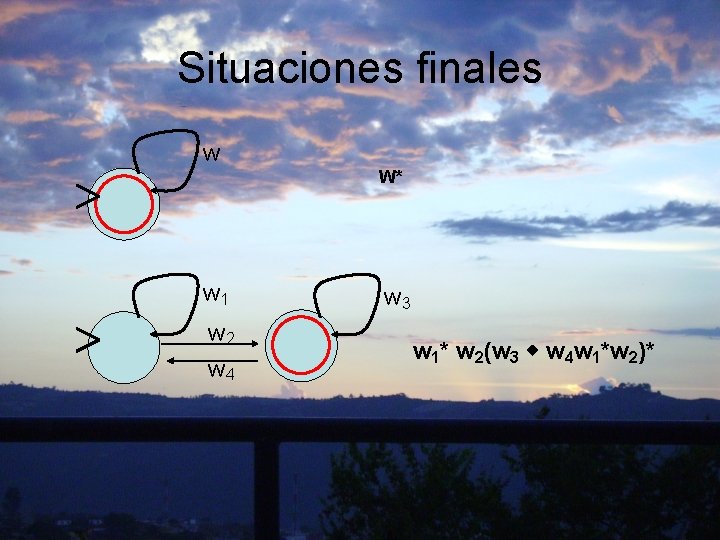
Situaciones finales w W* w 1 w 2 w 4 w 3 w 1* w 2(w 3 w 4 w 1*w 2)*

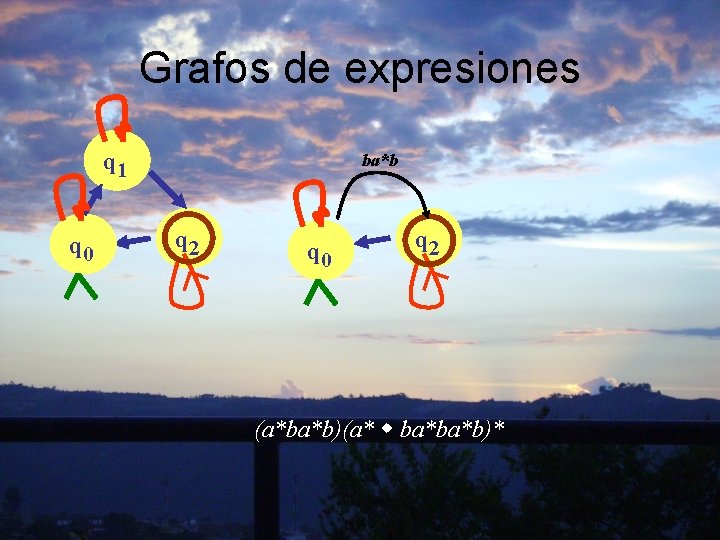
Grafos de expresiones q 1 q 0 ba*b q 2 q 0 q 2 (a*ba*b)(a* ba*ba*b)*

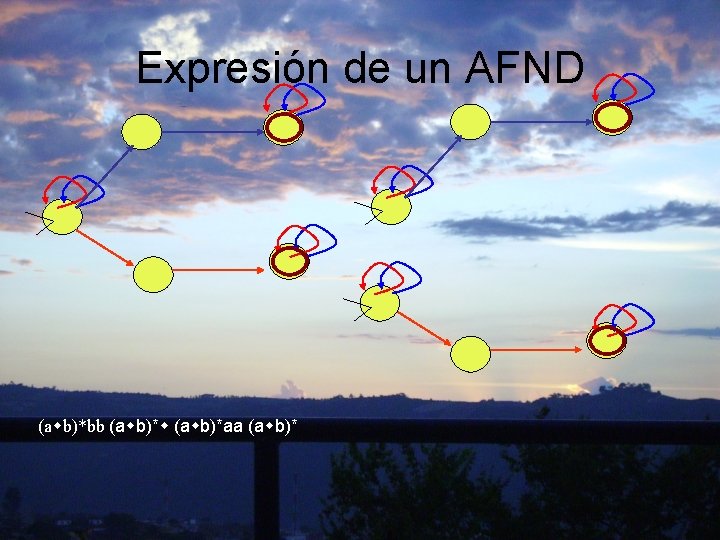
Expresión de un AFND (a b)*bb (a b)*aa (a b)*

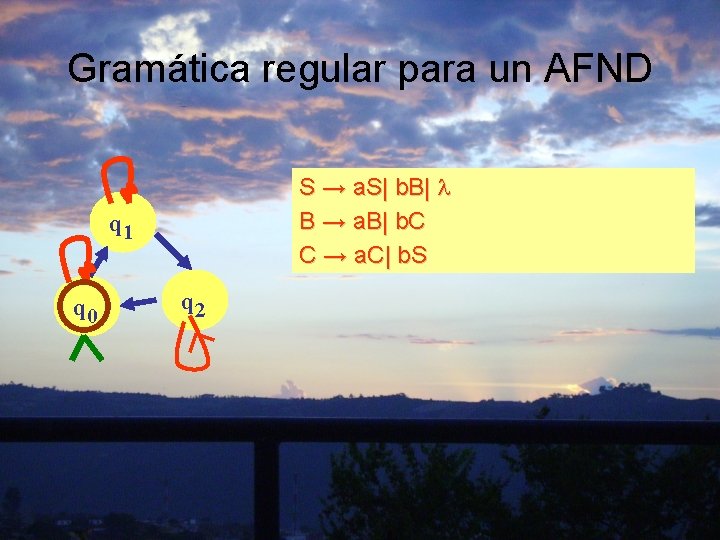
Gramática regular para un AFND S → a. S| b. B| B → a. B| b. C C → a. C| b. S q 1 q 0 q 2

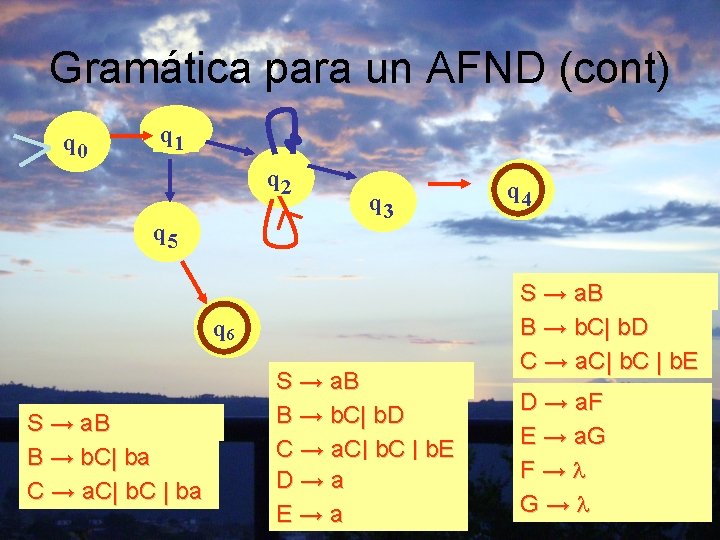
Gramática para un AFND (cont) q 0 q 1 q 2 q 5 q 3 q 6 S → a. B B → b. C| ba C → a. C| b. C | ba S → a. B B → b. C| b. D C → a. C| b. C | b. E D→a E→a q 4 S → a. B B → b. C| b. D C → a. C| b. C | b. E D → a. F E → a. G F→ G→

AFND para un gramática regular • Palabras sobre {a, b, c} que contiene al menos una c pero no contienen cc. S → a. S| b. S |c. A A → a. S| b. S| a, b q 0 a, b c q 1

Lenguajes regulares Expresiones Regulares AFD AFND Gramáticas Regulares No son LR:

Pre-Lema de bombeo • Sea w 1, w 2, w 3, w 4, …. y v 1, v 2, v 3, v 4, … sucesiones infinitas de palabras. • Si L es un lenguajes tal que wivj pertenece a L si y sólo sí i=j. • Entonces L no es regular. Si existiera un autómata finito de k estados existen i<j tal que *(q 0, wi)= *(q 0, wj) y por tanto wivi y wjvj son acptadas, contradicientdo las hipótesis.

Aplicación • No son regulares:

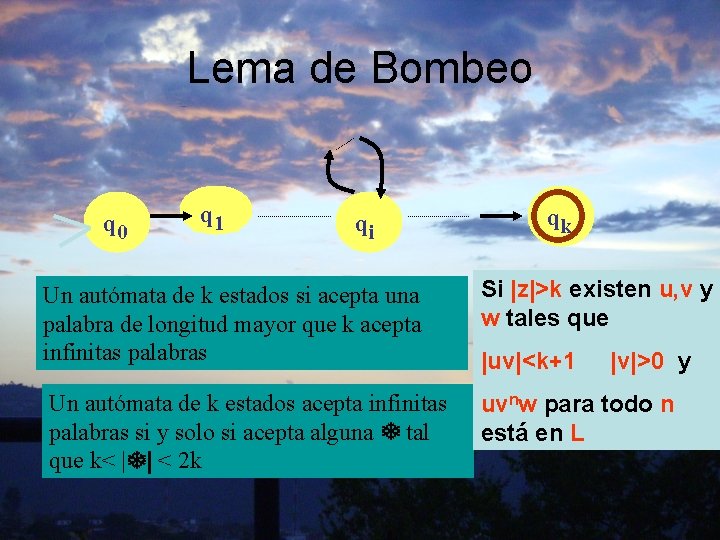
Lema de Bombeo q 0 q 1 qi qk Un autómata de k estados si acepta una palabra de longitud mayor que k acepta infinitas palabras Si |z|>k existen u, v y w tales que Un autómata de k estados acepta infinitas palabras si y solo si acepta alguna tal que k< | | < 2 k uvnw para todo n está en L |uv|<k+1 |v|>0 y

Aplicación • Las palabras cuya longitud es un cuadrado perfecto no forman un lenguaje regular. Supóngase que un autómata de k estados acepta tal lenguaje, tómese entonces una palabra z con longitud k 2 , entonces z=uvw con |uv| k o sea |v| k y además uv 2 w es aceptada por el autómata, Pero |uv 2 w| no puede ser cuadrado perfecto pues: |uv 2 w|= |uvw|+|v|=k 2+|v| k 2+k<(k+1 )2 2 2 Entre k y (k+1) no hay ningún cuadrado perfecto !

Propiedades de clausura Conjuntos finitos de palabras forman lenguajes regulares Unión de dos Concatenación de dos Intersección de dos Complemento de * de . . . lenguajes regulares, es un lenguaje regular