Aula 03 Aritmtica Computador de von Neumann Unidade

Aula 03 Aritmética

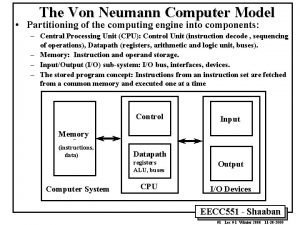
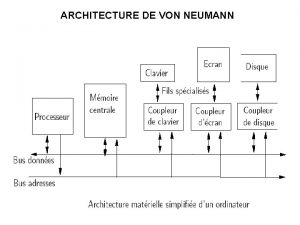
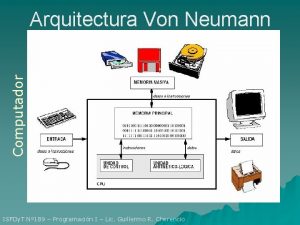
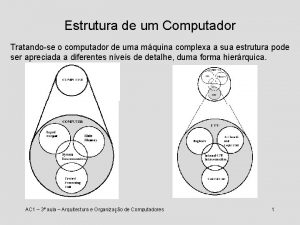
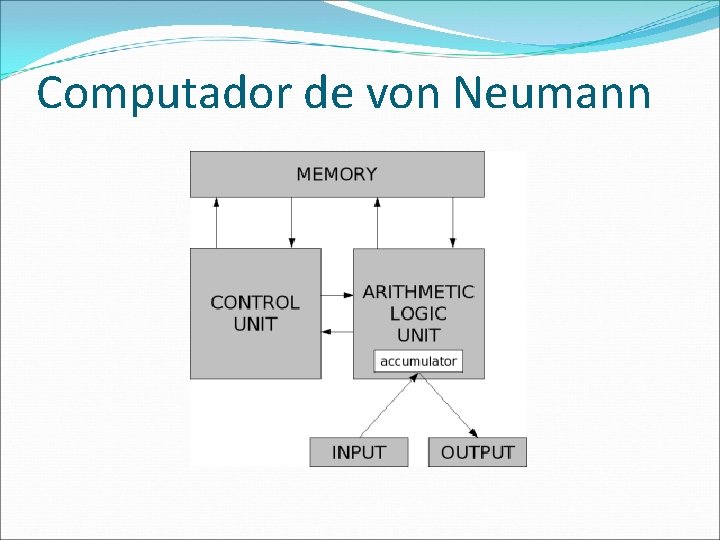
Computador de von Neumann

Unidade lógica e aritmética Diz respeito a: Desempenho (segundos, ciclos, instruções) Abstrações: Arquitetura do Conjunto de Instruções Linguagem Assembly e Linguagem de Máquina Para que serve: Implementar a Arquitetura operation a 32 ALU result 32 b 32

Aritmética MIPS • • Todas as instruções usa 3 registradores A ordem dos registradores é fixa (primeiro o registrador destino) Exemplo: C code: A = B + C MIPS code: add $s 0, $s 1, $s 2 (associado às variáveis pelo compilador)

Fluxo de Controle • Instrução slt – set on less than if $s 1 < $s 2 then $t 0 = 1 slt $t 0, $s 1, $s 2 else $t 0 = 0

Números Bits são apenas bits (sem nenhum significado inerente) — convenções definem a relação entre bits e números Números Binários (base 2) 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001. . . decimal: 0. . . 2 n-1 Naturalmente resultam em algumas sofisticações: números são finitos (overflow) números fracionários e reais números negativos p. ex. , no MIPS não existe instrução de subtração imediata - addi pode adicionar um número negativo) Como representamos números negativos? i. e. , que padrões de bits representam os números?

Possíveis Representações Sinal e Magnitude Complemento de 1 Complemento de 2 000 = +0 001 = +1 010 = +2 011 = +3 100 = -0 101 = -1 110 = -2 111 = -3 000 = +0 001 = +1 010 = +2 011 = +3 100 = -3 100 = -4 101 = -2 101 = -3 110 = -1 110 = -2 111 = -0 111 = -1 Comparações: balanceamento, número de zeros, facilidade de operações Qual é o melhor? Por que?

MIPS Números sinalizados de 32 bits: 0000 0000 two = 0 ten 0000 0000 0001 two = + 1 ten 0000 0000 0010 two = + 2 ten. . . 0111 1111 1111 1110 two = + 2, 147, 483, 646 ten 0111 1111 1111 two = + 2, 147, 483, 647 ten 1000 0000 0000 two = – 2, 147, 483, 648 ten 1000 0000 0000 0001 two = – 2, 147, 483, 647 ten 1000 0000 0000 0010 two = – 2, 147, 483, 646 ten. . . 1111 1111 1101 two = – 3 ten 1111 1111 1110 two = – 2 ten 1111 1111 two = – 1 ten maxint minint

Operações em Complemento de 2 Negar um número em complemento de 2: inverter todos os bits e somar 1 lembrança: “negar” e “inverter” são diferentes! Convertendo um número de n bits em números com mais de n bits: Um dado imediato de 16 bits do MIPS é convertido para 32 bits em aritmética Copiar o bit mais significativo (o bit de sinal) para outros bits 0010 -> 0000 0010 1010 -> 1111 1010 "sign extension"

Adição & Subtração Como no curso primário (carry/borrow) 0111 0110 + 0110 - 0101 Operações em complemento de 2 subtração usando soma de números negativos 0111 + 1010 Overflow (resultado muito grande para um computador de tamanho de palavra finito): P. ex. , somando dois números de n-bits não resulta em n-bits 0111 + 0001 1000 note que o bit de overflow é enganoso, ele não significa um carry de transbordo

Detectando Overflow Não ocorre overflow quando se soma um número positivo e um negativo quando os sinais são os mesmos para a subtração Overflow ocorre quando o valor afeta o sinal: quando somando dois positivos resulta num negativo ou, somando dois negativos resulta num positivo ou, subtraindo um negativo de um positivo e dá um negativo ou, subtraindo um positivo de um negativo e dá um positivo Considerar as operações A + B, e A – B Pode ocorrer overflow se B é 0 ? Pode ocorrer overflow se A é 0 ?

Efeitos do Overflow Uma exceção (interrupt) ocorre A instrução salta para endereço predefinido para a rotina de exceção O endereço da instrução interrompida é salvo para possível retorno Nem sempre se requer a detecção do overflow — novas instruções MIPS: addu, addiu, subu nota: addiu still sign-extends! nota: sltu, sltiu for unsigned comparisons

Revisão: Álgebra Booleana & Portas Problema: Considerar uma função lógica com 3 entradas: A, B, e C. A saída D é “true” se pelo menos uma entrada é “true” A saída E é “true” se exatamente duas entradas são “true” A saída F é “true” somente se todas as três entradas são “true” Mostrar a tabela verdade para essas três funções. Mostrar as equações Booleanas para as três funções. Mostrar uma implementação consistindo de portas inversoras, AND, e OR.

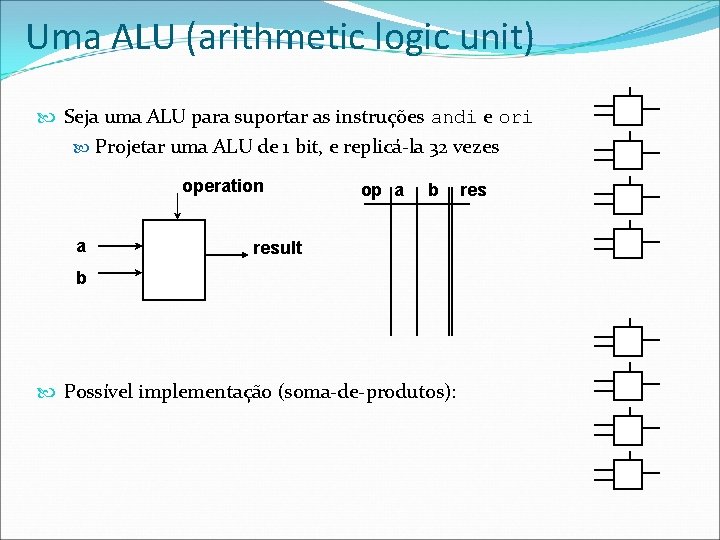
Uma ALU (arithmetic logic unit) Seja uma ALU para suportar as instruções andi e ori Projetar uma ALU de 1 bit, e replicá-la 32 vezes operation a op a b result b Possível implementação (soma-de-produtos): res

Revisão: Multiplexador Seleciona uma das entradas para a saída, baseado numa entrada de controle S A 0 B 1 C nota: mux de 2 -entradas embora tenha 3 entradas! Seja construir a nossa ALU usando um MUX:

Implementação de ALU de um bit Não é fácil decidir a “melhor” forma para construir algo Não queremos muitas entradas para uma única porta (fan-in) Não queremos distribuir para muitas portas (fan-out) Para o nosso propósito, facilidade de compreensão é importante Seja a ALU de 1 -bit para soma: cout = a b + a cin + b cin sum = a xor b xor cin Como construir uma ALU de 1 -bit para soma, AND e OR? Como construir uma ALU de 32 -bits?

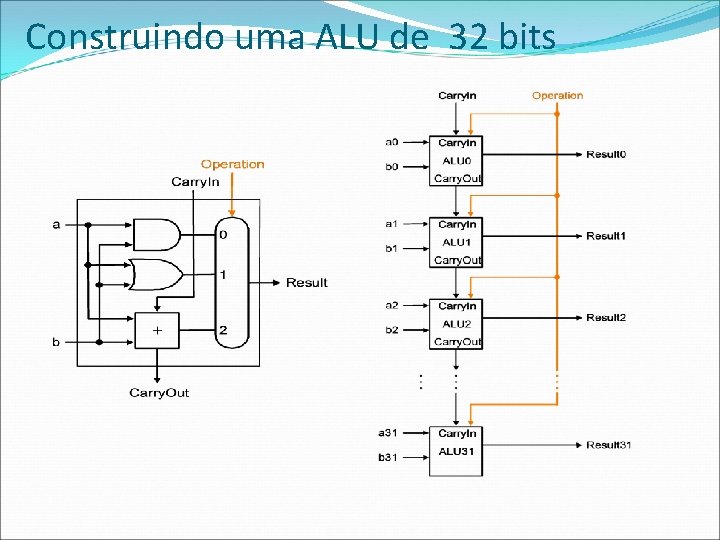
Construindo uma ALU de 32 bits

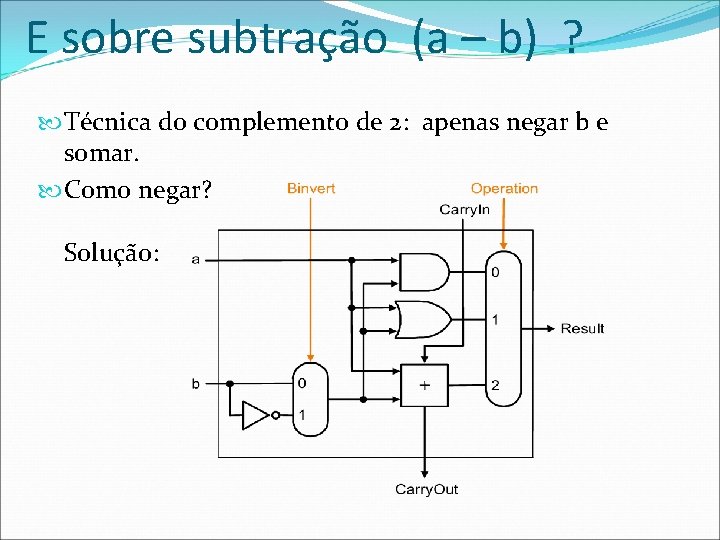
E sobre subtração (a – b) ? Técnica do complemento de 2: apenas negar b e somar. Como negar? Solução:

Outras operações da ALU do MIPS Deve suportar a instrução set-on-less-than (slt) lembrar: slt é uma instrução aritmética produz um 1 se rs < rt, e 0 caso contrário usar subtração: (a - b) < 0 implica a < b Deve suportar o teste para igualdade (beq $t 5, $t 6, $t 7) usar subtração: (a - b) = 0 implica a = b

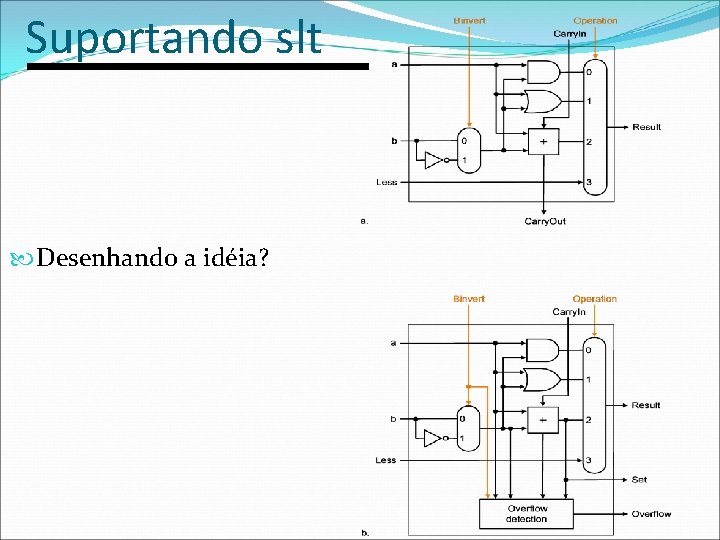
Suportando slt Desenhando a idéia?

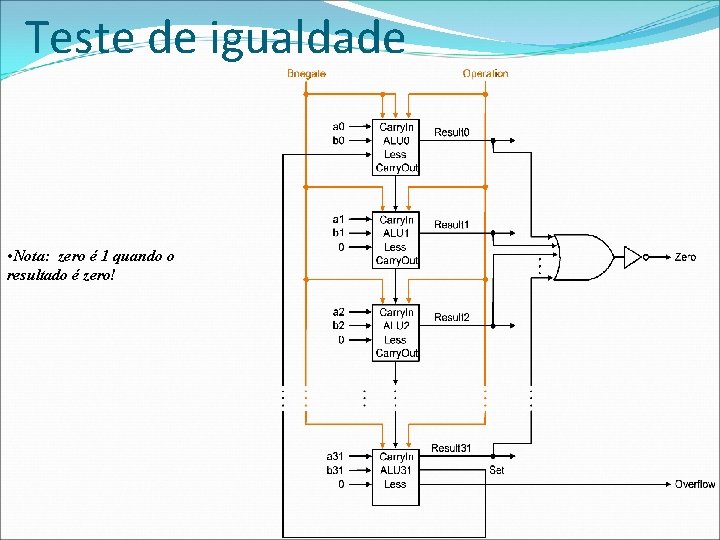
Teste de igualdade • Nota: zero é 1 quando o resultado é zero!

Linhas de controle Operation Binvert 000 = and 001 = or 010 = add 110 = subtract 111 = slt

Conclusão Podemos construir uma ALU para suportar o conjunto de instruções MIPS -- usando multiplexador para selecionar a saída desejada realizando uma subtração usando o complemento de 2 replicando uma ALU de 1 -bit para produzir uma ALU de 32 -bits Pontos importantes sobre o hardware Todas as portas estão sempre trabalhando A velocidade de uma porta é afetada pelo número de entradas da porta A velocidade de um circuito é afetado pelo número de portas em série (no caminho crítico ou nivel mais profundo da lógica) Mudanças inteligentes na organização pode melhorar o desempenho

Problema: somador ripple carry (vai-um propagado) é lento Uma ALU de 32 -bits é tão rápida quanto uma ALU de 1 -bit? Existem mais de uma forma de somar? dois extremos: ripple carry e soma-de-produtos Voce pode ver a propagação do vai-um? Como resolvê-lo? c 1 = a 0 c 0 + b 0 c 0 + a 0 b 0 = (a 0 + b 0)c 0 + a 0 b 0 c 2 = a 1 c 1 + b 1 c 1 + a 1 b 1 c 3 = a 2 c 2 + b 2 c 2 + a 2 b 2 c 4 = a 3 c 3 + b 3 c 3 + a 3 b 3

Somador de vai-um antecipado (Carry-lookahead) - CLA Uma técnica intermediária entre dois extremos Motivação: Se não sabemos o valor do carry-in, o que fazemos? Quando sempre geramos um carry? gi = ai bi Quando propagamos um carry? pi = ai + bi Resolvemos o ripple calculando o vai-um antecipadamente, usando as equações: c 1 = g 0 + p 0 c 0 c 2 = g 1 + p 1 c 1 c 3 = g 2 + p 2 c 2 c 4 = g 3 + p 3 c 3

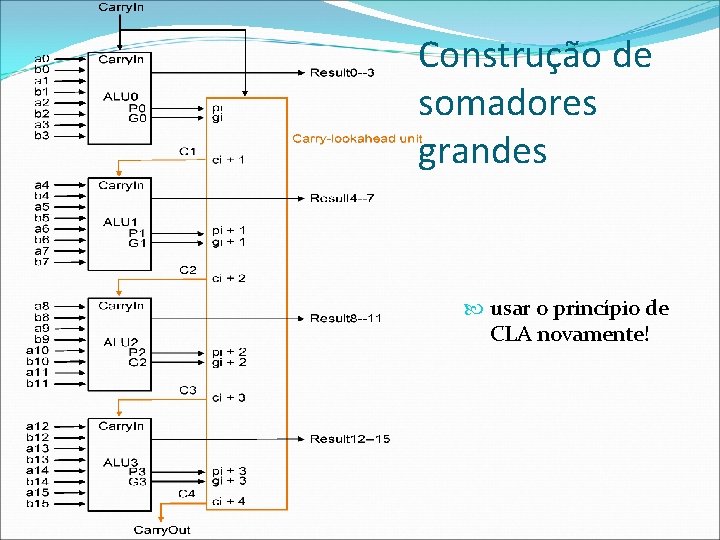
Construção de somadores grandes usar o princípio de CLA novamente!

Multiplicação Mais complicado que soma Realizado via deslocamento e soma Mais tempo e mais área Vejamos 3 versões baseados no algoritmo 0010 __x_1011 (multiplicando) (multiplicador) Números negativos: converter e multiplicar

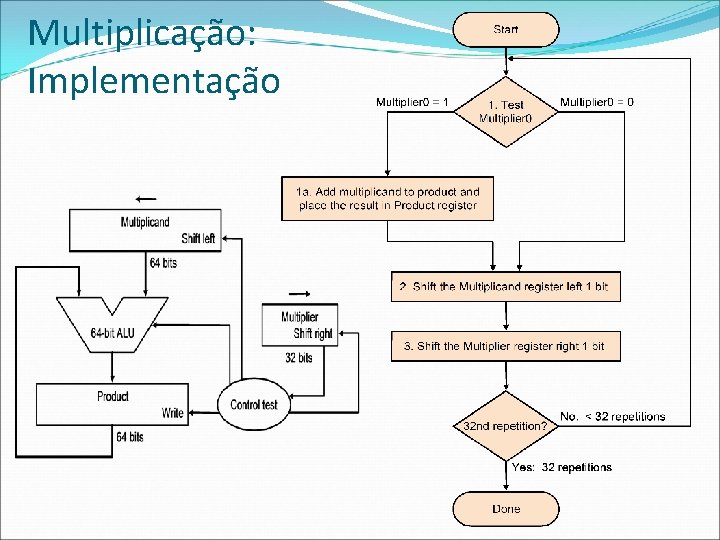
Multiplicação: Implementação

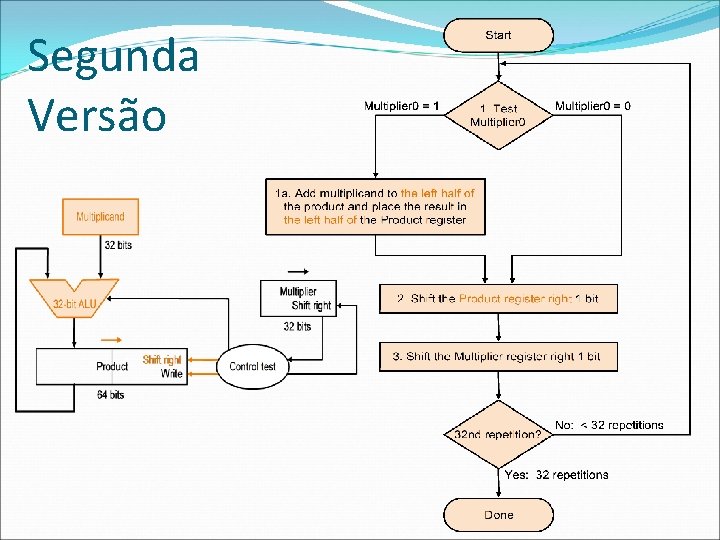
Segunda Versão

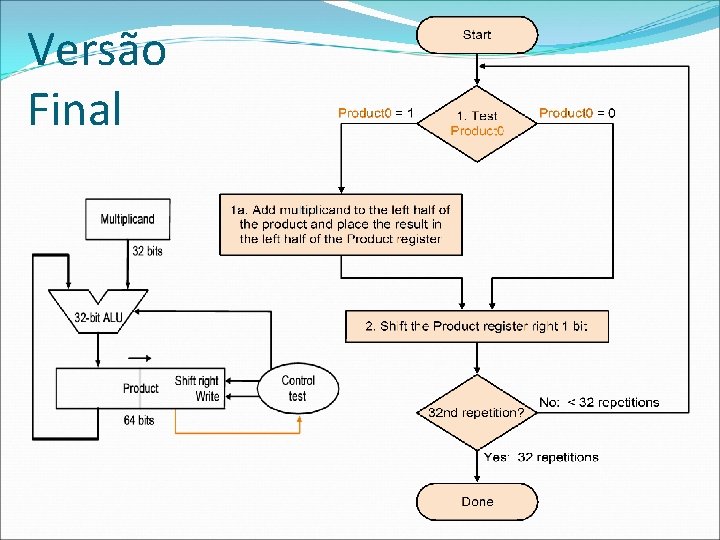
Versão Final

Multiplicação Paralela a 5 a 4 a 3 a 2 a 1 a 0 = A x b 5 b 4 b 3 b 2 b 1 b 0 = B __________________ a 5 b 0 a 4 b 0 a 3 b 0 a 2 b 0 a 1 b 0 a 0 b 0 = W 1 a 5 b 1 a 4 b 1 a 3 b 1 a 2 b 1 a 1 b 1 a 0 b 1 = W 2 a 5 b 2 a 4 b 2 a 3 b 2 a 2 b 2 a 1 b 2 a 0 b 2 = W 3 a 5 b 3 a 4 b 3 a 3 b 3 a 2 b 3 a 1 b 3 a 0 b 3 = W 4 a 5 b 4 a 4 b 4 a 3 b 4 a 2 b 4 a 1 b 4 a 0 b 4 = W 5 a 5 b 5 a 4 b 5 a 3 b 5 a 2 b 5 a 1 b 5 a 0 b 5 = W 6 _________________________________ P 11 P 10 P 9 P 8 P 7 P 6 P 5 P 4 P 3 P 2 P 1 P 0 = Ax. B=P

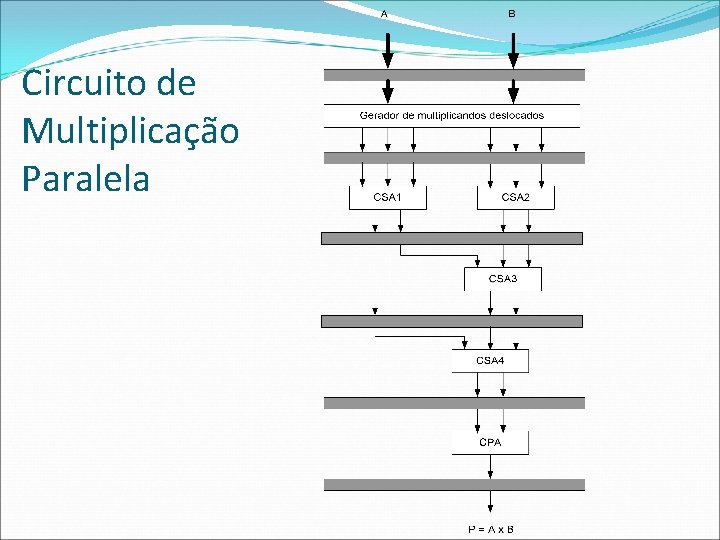
Somadores CPA – Carry Propagation Adder Faz a adição de 2 números A e B para produzir o resultado A + B. CSA – Carry Save Adder Faz a adição de 3 números A, B e D, produzindo dois resultados: soma S e vai-um C. Matematicamente, tem-se A + B + D = S + C. A = 1 1 0 1 B = 0 1 1 0 D = 1 1 0 1 1 1 _____________ C = 1 1 0 1 1 1 S = 0 1 1 1 0 0 _____________ A + B + D = S + C = 1 0 0 0 1 0

Circuito de Multiplicação Paralela

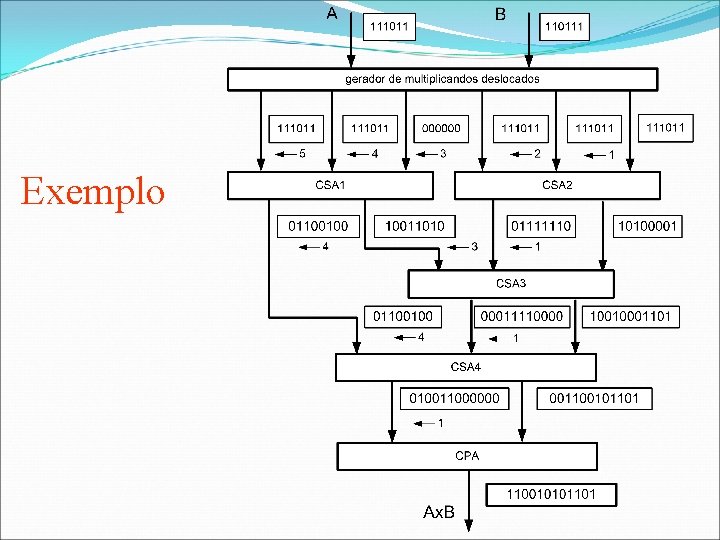
Exemplo

Ponto Flutuante Necessitamos de uma forma para representar Números com frações, p. ex. , 3. 1416 Números muito pequenos, p. ex. , . 00001 Números muito grandes, p. ex. , 3. 15576 ´ 109 Representação: Sinal, expoente, significando: (– 1)sinal ´ significando ´ 2 expoente Mais bits para o significando dá mais resolução Mais bits para o expoente aumenta o intervalo (range) Padrão ponto flutuante IEEE 754: Precisão simples: expoente de 8 bits, significando de 23 bits Precisão dupla: expoente de 11 bits, significando de 52 bit

Padrão de ponto flutuante IEEE 754 O primeiro bit (leading bit), “ 1” do significando é implícito Expoente é “polarizado” para fazer a separação facilmente bias de 127 para precisão simples e 1023 para precisão dupla Resumo: (– 1)sinal ´ (1+significando) ´ 2 expoente – bias Exemplo: decimal: -. 75 = -3/4 = -3/22 binário: -. 11 = -1. 1 x 2 -1 Ponto flutuante: expoente = 126 = 01111110 Precisão simples IEEE: 101111110100000000000

Complexidade do Ponto Flutuante Além do overflow tem “underflow” Precisão pode ser um grande problema IEEE 754 mantem dois extra bits, guard e round Quatro modos de arredondamento positivo dividido por zero resulta em “infinito” zero dividido por zero resulta em “not a number” Outras complexidades A Implementação do padrão pode ser complicado Não usar o padrão pode ser mesmo pior

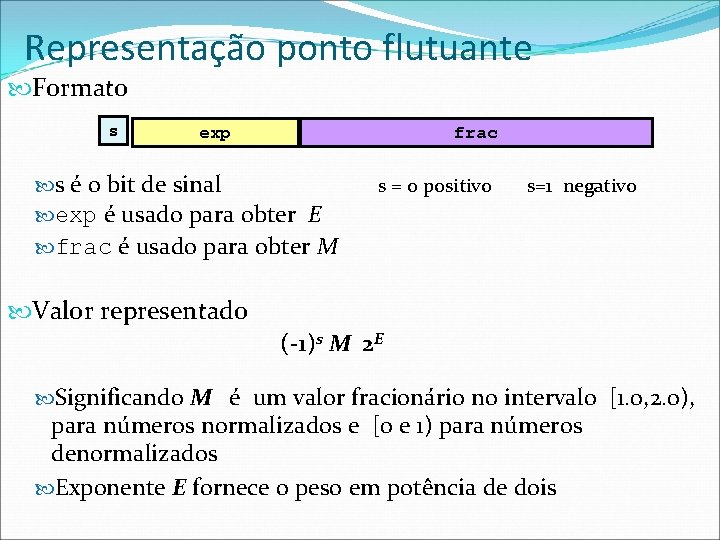
Representação ponto flutuante Formato s exp frac s é o bit de sinal s = 0 positivo s=1 negativo exp é usado para obter E frac é usado para obter M Valor representado (-1)s M 2 E Significando M é um valor fracionário no intervalo [1. 0, 2. 0), para números normalizados e [0 e 1) para números denormalizados Exponente E fornece o peso em potência de dois

Valores numéricos Normalizados Condição exp 000… 0 e exp 111… 1 Expoente codificado como valor polarizado (biased) E = exp – bias exp : valor não sinalizado bias : valor da polarização Precisão Simples: 127 (exp: 1… 254, E: -126… 127) Precisão dupla: 1023 (exp: 1… 2046, E: -1022… 1023) Em geral: bias = 2 e-1 - 1, onde e e´ o numero de bits do expoente Significando codificado com bit 1 mais significativo (leading bit) implicito M = 1. xxx…x 2 xxx…x: bits da frac Minimo quando 000… 0 (M = 1. 0) Maximo quando 111… 1 (M = 2. 0 – ) O bit extra (leading bit 1) e´ obtido “implicitamente”

Valores denormalizados Condição exp = 000… 0 Valor do Expoente E = –Bias + 1 Valor do Significando M = 0. xxx…x 2 xxx…x: bits de frac Casos exp = 000… 0, frac = 000… 0 Representa valor 0 Nota-se que existem valores distintos +0 e – 0 exp = 000… 0, frac 000… 0 Numeros muito próximos de 0. 0 Perde precisão à medida que vai diminuindo “ underflow gradual”

Valores especiais Condição exp = 111… 1 Casos exp = 111… 1, frac = 000… 0 Representa valor (infinito) Operação que transborda (overflow) Ambos positivo e negativo P. ex. , 1. 0/0. 0 = 1. 0/ 0. 0 = + , 1. 0/ 0. 0 = exp = 111… 1, frac 000… 0 Not-a-Number (Na. N) Nenhum valor numérico pode ser determinado P. ex. , sqrt(– 1),

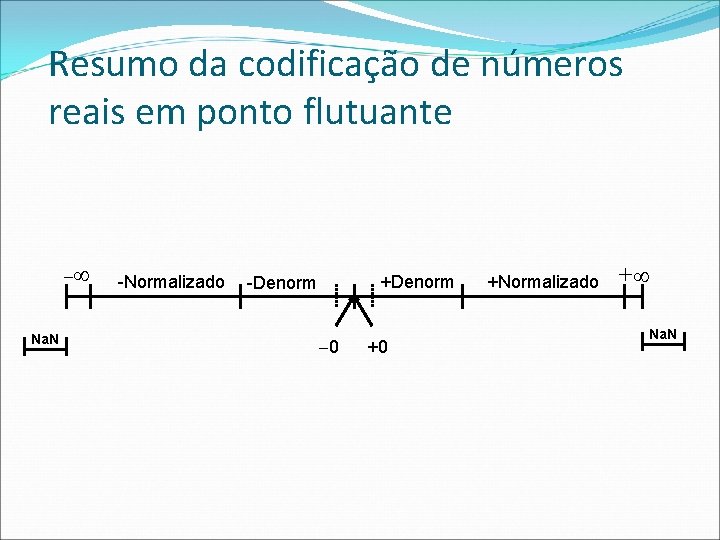
Resumo da codificação de números reais em ponto flutuante Na. N -Normalizado +Denorm -Denorm 0 +0 +Normalizado + Na. N

Representação ilustrativa de 8 bits Representação ponto flutuante de 8 bits O bit de sinal e´ o bit mais significativo. Os seguintes quatro bits são expoente, com bias de 7. Os últimos três bits são frac Semelhante a forma geral no formato IEEE normalizado, denormalizado Representação de 0, Na. N, infinito 7 6 s 0 3 2 exp frac

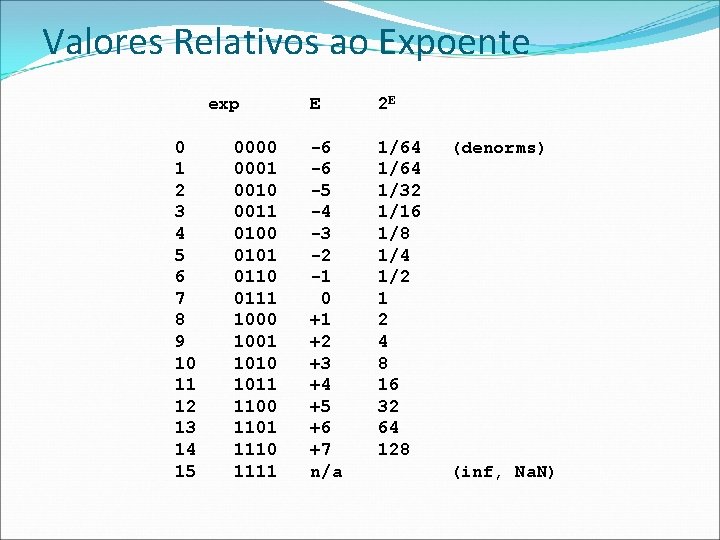
Valores Relativos ao Expoente exp 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 E 2 E -6 -6 -5 -4 -3 -2 -1 0 +1 +2 +3 +4 +5 +6 +7 n/a 1/64 1/32 1/16 1/8 1/4 1/2 1 2 4 8 16 32 64 128 (denorms) (inf, Na. N)

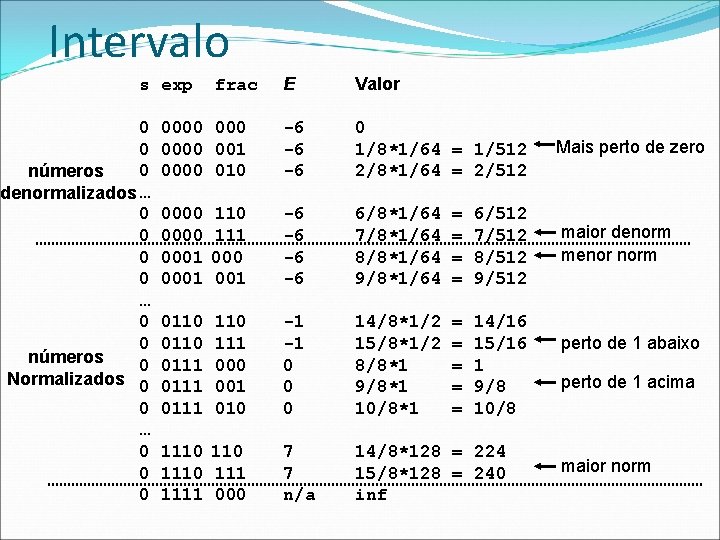
Intervalo E Valor 0000 001 0000 010 -6 -6 -6 0 1/8*1/64 = 1/512 2/8*1/64 = 2/512 Mais perto de zero 0000 0001 110 111 000 001 -6 -6 6/8*1/64 7/8*1/64 8/8*1/64 9/8*1/64 = = 6/512 7/512 8/512 9/512 maior denorm menor norm 0110 0111 110 111 000 001 010 -1 -1 0 0 0 14/8*1/2 15/8*1/2 8/8*1 9/8*1 10/8*1 = = = 14/16 15/16 1 9/8 10/8 7 7 n/a 14/8*128 = 224 15/8*128 = 240 inf s exp 0 0 0 números denormalizados … 0 0 números 0 Normalizados 0 0 … 0 0 0 frac 1110 1111 000 perto de 1 abaixo perto de 1 acima maior norm

Distribuição de valores Formato de 6 -bits tipo IEEE e = 3 bits de expoente f = 2 bits de fracao bias e´ 3 Notar como a distribuição fica mais densa perto de zero.

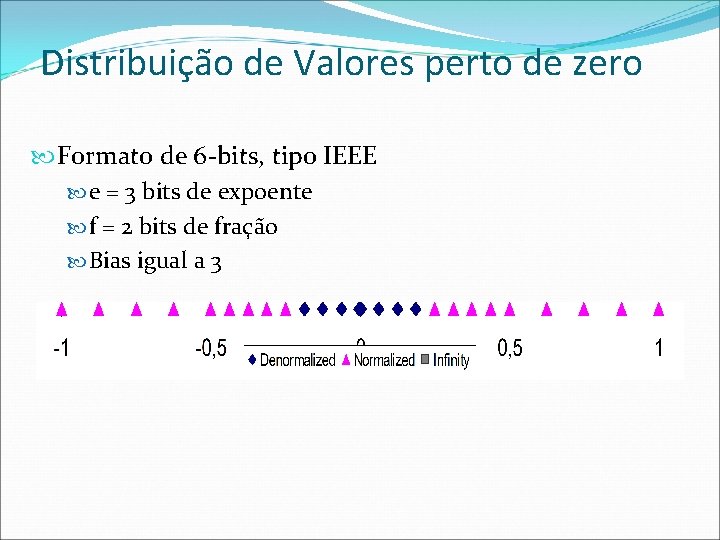
Distribuição de Valores perto de zero Formato de 6 -bits, tipo IEEE e = 3 bits de expoente f = 2 bits de fração Bias igual a 3

Numeros interessantes Descrição exp frac Zero 00… 00 menor Pos. Denorm. 00… 00 {126, 1022} valor numérico 0. 0 00… 01 2– {23, 52} X 2– Single 1. 4 X 10– 45 Double 4. 9 X 10– 324 maior Denorm. 00… 00 11… 11 Single 1. 18 X 10– 38 (1. 0 – ) X 2– {126, 1022} Double 2. 2 X 10– 308 menor Pos. Norm. 00… 01 00… 00 Um 01… 11 00… 00 maior Normalized 11… 10 11… 11 Single 3. 4 X 1038 1. 0 X 2– {126, 1022} 1. 0 (2. 0 – ) X 2{127, 1023} Double 1. 8 X 10308

Operações em ponto flutuante Conceitualmente Primeiro computar o resultado exato Fazê-lo enquadrar na precisão desejada transborda se o expoente for muito grande arredonda para caber no frac Modos de arredondamento 1. 40 Zero 1 Round down (- ) 1 Round up (+ ) 2 Nearest Even (default) 1 1. 60 1 1 2 2 1. 50 1 1 2 2 2. 50 2 2 3 2 – 1. 50 – 1 – 2 Nota: 1. Round down: resultado e´perto mas não maior que o resultado verdadeiro. 2. Round up: resultado e´perto mas não menor do que o resultado verdadeiro.

Multiplicação em FP Operandos * (– 1)s 1 M 1 2 E 1 (– 1)s 2 M 2 2 E 2 Resultado exato (– 1)s M 2 E Sinal s: s 1 xor s 2 Significando M: M 1 * M 2 Expoente E: E 1 + E 2 Representação final se M ≥ 2, deslocar à direita M, incrementar E se E fora do intervalo, overflow Arredonda M para caber em frac

Adição FP Operandos (– 1)s 1 M 1 2 E 1 E 1–E 2 (– 1)s 2 M 2 2 E 2 (– 1)s 1 M 1 Assumir E 1 > E 2 (– 1)s 2 M 2 + Resultado exato (– 1)s M 2 E (– 1)s M Sinal s, significando M: Resultado de alinhamento e adição Expoente E: E 1 Representação final Se M ≥ 2, deslocar à direita M, incrementa E Se M < 1, deslocar à esquerda M de k posições, decrementar E de k Overflow se E fora do intervalo arredonda M para caber em frac

Ariane 5 Explodiu 37 segundos após decolagem Por que? Foi computada a velocidade horizontal como número em ponto flutuante Convertido para inteiro de 16 -bits Funcionou bem para Ariane 4 Ocorreu Overflow para Ariane 5 Foi usado o mesmo software