Asymptotically optimal Kkpackings of dense graphs via fractional

Asymptotically optimal Kk-packings of dense graphs via fractional Kk-decompositions Raphael Yuster University of Haifa 1

Fractional decompositions of dense hypergraphs Raphael Yuster University of Haifa 2

Definitions, notations and background • Let H 0 be a fixed hypergraph. A fractional H 0 -decomposition of a hypergraph H is an assignment of nonnegative real weights to the copies of H 0 in H such that for each e E(H) the sum of the weights of copies of H 0 containing e is 1. • K(k, r) will denote the complete r-graph with k vertices. We think of k and r as fixed. • We prove (for n > n 0): There exists a positive constant α=α(k, r) so that every r-graph in which every (r-1)-set is contained in at least n(1 -α) edges has a fractional K(k, r)-decomposition. • In fact: α(k, r) > 6 -kr α(k, 2) > 0. 1 k -10 α(3, 2) > 10 -4 3

From fractional to integral • Combined with the following result of Haxell, Nagle and Rödl, our result has consequences for integral packing. • Let ν(H 0, H) denote the maximum number of edge-disjoint copies of H 0 in H (the H 0 -packing number of H). • Let ν*(H 0, H) denote the fractional relaxation. • Trivially, ν*(H 0, H) ≥ ν(H 0, H). • If H is an r-graph with n vertices (r=2, 3) it has been proved by Haxell, Nagle and Rödl that ν*(H 0, H) < ν(H 0, H) + o(nr). 4

Corollaries for graphs • If G is a graph with n vertices, and δ(G) > (1 - 0. 1 k -10)n then G has an asymptotically optimal Kk-packing. • Same theorem holds for k-vertex graphs. • For triangles (k=3), δ(G) > 0. 9999 n suffices. • The previously best known bound (for the missing degree) in the triangles case was 10 -24 (Gustavsson). The previously best known bound for Kk was 10 -37 k-94 (Gustavsson). • However, Gustavsson guarantees a decomposition in case the appropriate divisibility conditions holds. 5

Corollary for 3 -graphs • If H is a 3 -graph with n vertices and minimum co-degree (1 -216 -k)n then H has an asymptotically optimal K(k, 3)-packing. • Same theorem holds for k-vertex 3 -graphs. • The previously best known bound (for the missing co-degree) was 0 (Rödl). 6

Tools used in the proof • Some linear algebra. • Kahn’s Theorem: For every r* > 1 and every γ > 0 there exists a positive constant ρ=ρ(r*, γ) such that the following statement is true: If U is an r*-graph with: maxdeg < D maxcodeg < ρD then there is a proper coloring of the edges of U with at most (1+γ)D colors. • Several probabilistic arguments. • Hall’s Theorem for hypergraphs by Aharoni and Haxell (topological proof): Let U={U 1, …, Um} be a family of p-graphs. If for every W U there is a matching in UU WU of size greater than p(|W|-1) then U has an SDR. 7

The proof Recall the goal There exists a positive constant α=α(k, r) so that every r-graph in which every (r-1)-set is contained in at least n(1 -α) edges has a fractional K(k, r)-decomposition. • Let t=k(r+1) Consider the 3 r-graphs: F(k, r) = { K(k, r), K(t, r), H(t, r) } H(t, r) is a K(t, r) missing one edge. • K(k, r) fractionally decomposes each element of F(k, r). (To show that K(k, r) fractionally decomposes H(t, r) requires some work. Here we use some linear algebra. ) • For r=2 it suffices to take t=2 k-1 and the proof is easy. E. g. K 5 - fractionally decomposes K 3. 8

The proof – cont. It suffices to prove the stronger theorem There exists a positive constant α=α(k, r) so that every r-graph in which every (r-1)-set is contained in at least n(1 -α) edges has an integral F(k, r)-decomposition. • Let ε = ε(k, r) be chosen later. • Let η = (2 -H(ε)0. 9)1/ε. H(ε) the entropy function. • Let α = min{ (η/2)2 , ε 2/(t 24 t+1) } • Let γ satisfy (1 -αt 2 t)(1 -γ)/(1+γ)2 > 1 -2αt 2 t • Let r* = • Let ρ = ρ(r*, γ) be the constant from Kahn’s theorem. • Assume n is suff. large as a function of all these constants. • Let δd(H) and Δd(H) denote the min and max 9 d-degrees of H, 0 < d < r, resp.

The proof – cont. • Our r-graph H satisfies δd(H) > • It is not difficult to prove (induction) that every edge of H lies on “many” K(t, r). In fact, if c(e) denotes the number of K(t, r) containing e then nt-r > c(e) (t-r)! > nt-r(1 -αt 2 t) • Color the edges of H randomly using q=n 1/(4 r*-4) colors (that’s many colors). • Let Hi be the spanning r-graph colored with i. • Easy (Chernoff): δd(Hi) very close to δd(H)/q • Not so easy: we would also like to show that ci(e) is very close to its expectation c(e)n-1/4. Note that two K(t, r) that contain e may share other edges as well – a lot of dependence. 10

The proof – cont. • Still, we can prove it by partitioning the c(e) events to many (but not too many) subsets such that all events in the same part are independent, show large deviation on each part and the sum of slacks is still negligible. Thus, (1+γ)nt-r-1/4 > ci(e) (t-r)! > (1 -γ)nt-r-1/4(1 -αt 2 t) • We fix the coloring with q colors satisfying the above. • For each Hi we create another r*-graph Ui as follows: - the vertices of Ui are the edges of Hi - the edges of Ui are the copies of K(t, r) in Hi • Notice that Δ(Ui) < D=(1+γ)nt-r-1/4 (t-r)!-1 Notice that Δ 2(Ui) < nt-r-1 << ρD 11

The proof – cont. • By Kahn’s theorem this means that the K(t, r) copies of Hi can be partitioned into at most D(1+γ) packings. • We pick one of these packings at random. Denote it by Li. • The set L=L 1 U…U Lq is a K(t, r) packing of H. • Let M denote the edges of H not belonging to any element of L. • Let p = • A p-subset {S 1, …, Sp} of L is good for e M if we can select one edge from each Si such that, together with p, we have a K(k, r). • We say that L is good if for each e M we can select a good p-subset, and all |M| selections are disjoint. 12

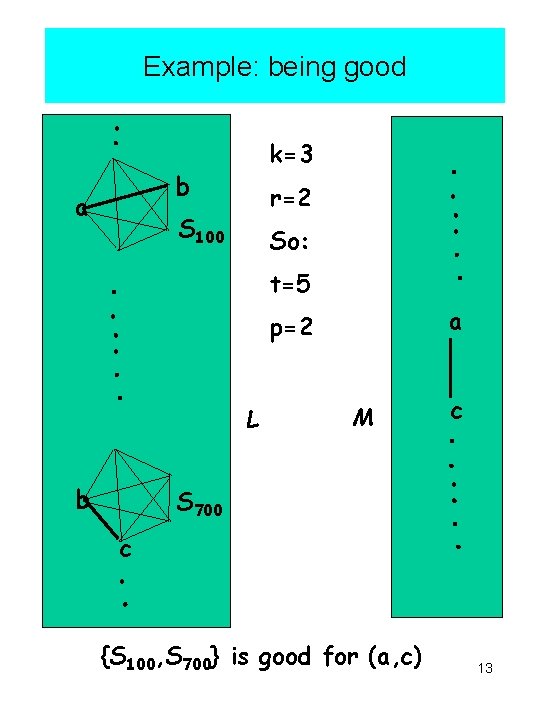
Example: being good k=3 b a r=2 S 100 So: t=5 a p=2 L b M c S 700 c {S 100, S 700} is good for (a, c) 13

The proof – cont. • Recall F(k, r) = { K(k, r), K(t, r), H(t, r) }. Clearly: L is good → H has an Fk-decomposition. • It remains to show that there exists a good L. We will show that with positive probability, the random selection of the q packings L 1 U…U Lq yields a good L. • We use Hall’s theorem for hypergraphs. • Let M={e 1, …, em}. • Let U={U 1, …, Um} be a family of p-graphs defined as follows: • The vertex set of Ui is L (i. e, K(t, r) copies) • The edge set of Ui are the p-subsets of L that are good for ei • U has an SDR → L is good. 14

The proof – cont. • Thus, it suffices to show that the random selection of the q packings L 1 U…U Lq guarantees that, with positive probability, for every W U there is a matching in UU WU of size greater than p(|W|-1). • It turns out that the only thing needed to guarantee this is to show that with positive probability, for all 1 < d < r: Δd(H[M]) < 2ε • Once this is established, the remainder of the claim is deterministic, namely • Δd(H[M]) < 2ε → U has an SDR. (purely combinatorial proof, but not so easy). 15

Open problems • Determine the correct value of α(k, r). • The simplest case is α(3, 2) (triangles). We currently have α(3, 2) > 10 -4. • A construction shows that α(3, 2) ≤ ¼. • More generally, a construction given in the paper shows that α(k, 2) ≤ 1/(k+1). We conjecture α(k, 2) = 1/(k+1). • For hypergraphs we don’t even know what to conjecture. 16