Analysis of the Rossler system Chiara Mocenni The

Analysis of the Rossler system Chiara Mocenni

The Rossler equations Considering only the first two equations and assuming small z, we have:

The reduced system It is equivalent to the oscillator: With eigenvalues: • For a=0 the oscilator is harmonic (centers) • For a>0 the oscillator is undamped (unstable spirals) • Consider 0<a<2

Geometry of the phase space In the 3 D phase space this fact induces a stretching mechanism This fact is non sufficient by itself to produce the chaotic behavior because in the linear case this instability is not compensated by any other folding mechanism. The system is globally unstable A nonlinear stabilizing term is necessary for maintaining the trajectories confined in a region of the 3 D phase space

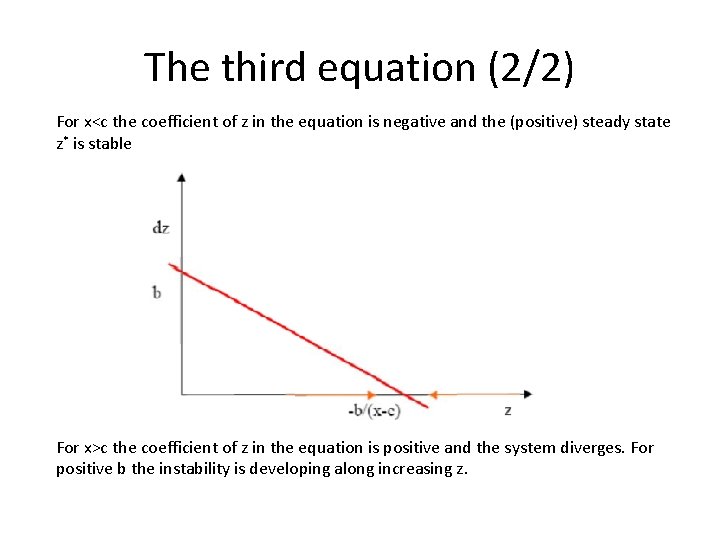
The third equation (1/2) The folding is produced by the term associated to parameter c in the third equation Consider only the equation for z and assume b>0 The equation for z has the steady state

The third equation (2/2) For x<c the coefficient of z in the equation is negative and the (positive) steady state z* is stable For x>c the coefficient of z in the equation is positive and the system diverges. For positive b the instability is developing along increasing z.

The complete system Assume fixed b and c and vary parameter a • b=2 • c=4 The system has two steady states, that exist for • a≠ 0 • a < c 2/4 b

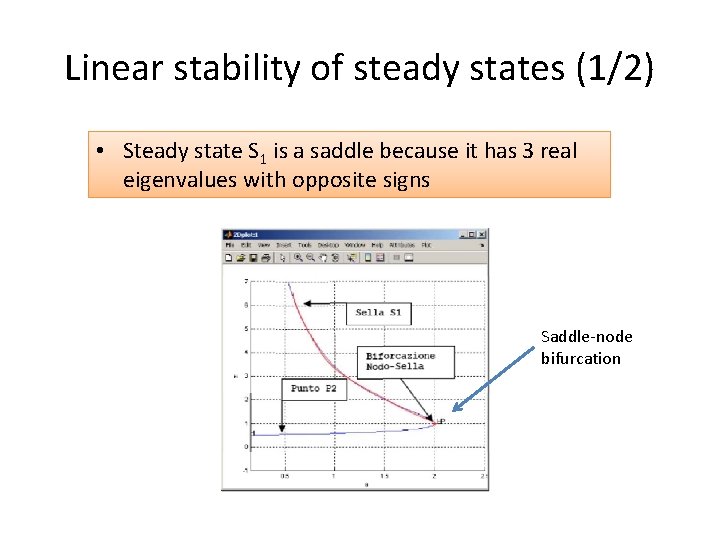
Stability of the steady states • Assume 0 < a < c 2/4 b • Let S 1 be the steady state (x 1, y 1, z 1) • Let P 2 be the steady state (x 2, y 2, z 2) • Let A be the Jacobian matrix

The steady states • For a = c 2/4 b S 1 and P 2 coincide and for a > c 2/4 b disappear

Linear stability of steady states (1/2) • Steady state S 1 is a saddle because it has 3 real eigenvalues with opposite signs Saddle-node bifurcation

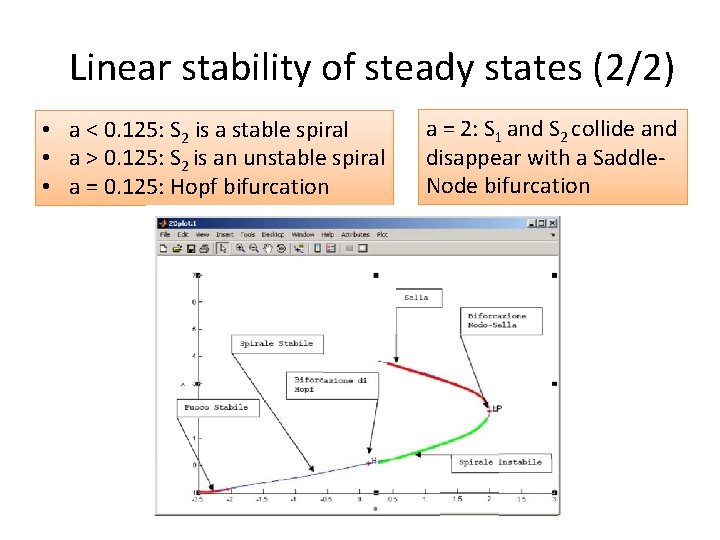
Linear stability of steady states (2/2) • a < 0. 125: S 2 is a stable spiral • a > 0. 125: S 2 is an unstable spiral • a = 0. 125: Hopf bifurcation a = 2: S 1 and S 2 collide and disappear with a Saddle. Node bifurcation

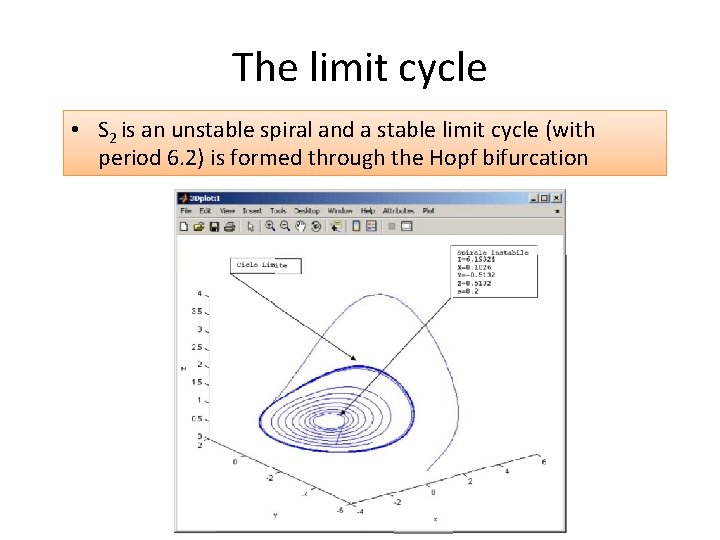
The limit cycle • S 2 is an unstable spiral and a stable limit cycle (with period 6. 2) is formed through the Hopf bifurcation

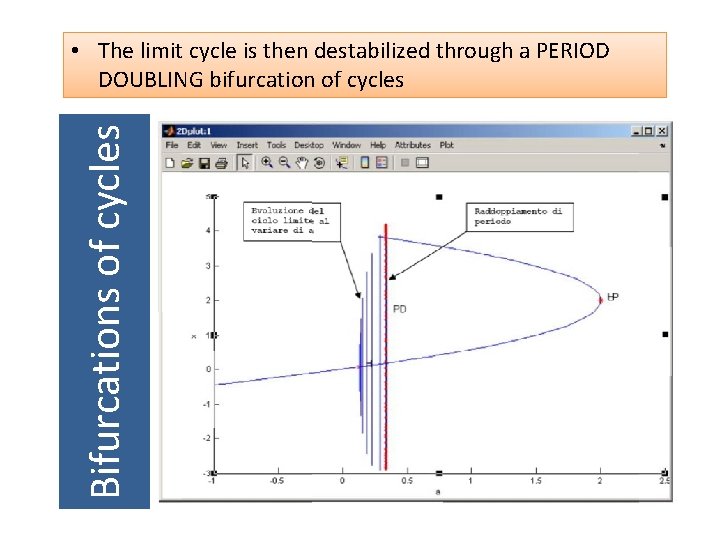
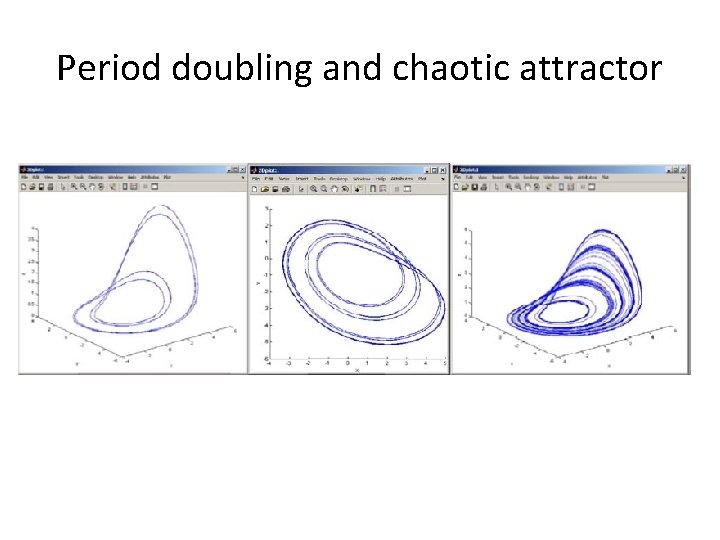
Bifurcations of cycles • The limit cycle is then destabilized through a PERIOD DOUBLING bifurcation of cycles

Explaining the mechanisms • This fact is due to the mechanism shown by equation 3, that is activated for x = c (in our example c = 4) • The limit cycle grows for increasing a, and when x = 4 the variable z is destabilized, producing a divergence of the trajectories along z • At this point a stabilizing mechanism on x is induced by equation 1 and leading again z to enter the stable region • The result of this combination of mechanisms induces that a double period limit cycle is formed

Stretching and Folding (1/2)

Stretching and Folding (2/2)

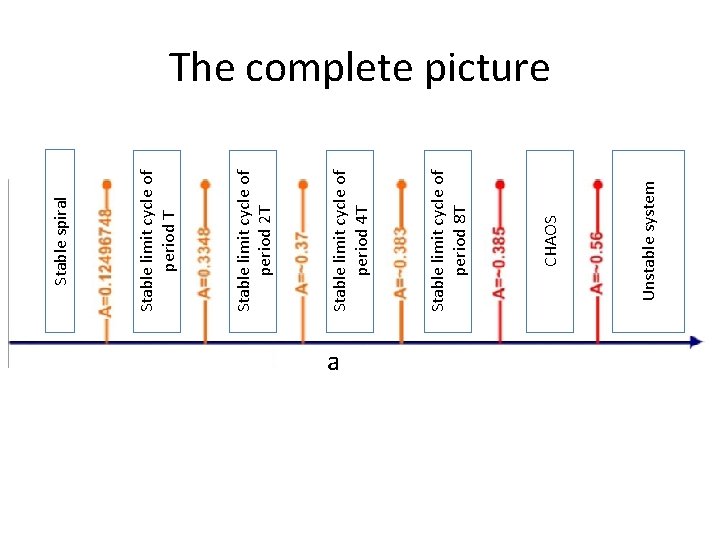
a Unstable system CHAOS Stable limit cycle of period 8 T Stable limit cycle of period 4 T Stable limit cycle of period 2 T Stable limit cycle of period T Stable spiral The complete picture

Period doubling and chaotic attractor

The Rossler attractor: a movie