Analiza informacji meteorologicznych Wykad 6 Krzysztof Markowicz Instytut




















- Slides: 28

Analiza informacji meteorologicznych Wykład 6 Krzysztof Markowicz Instytut Geofizyki UW kmark@igf. fuw. edu. pl

3 -wymiarowa analiza wariacyjna : 3 D-VAR • W metodzie 3 D-Var poszukujemy wektora analizy xa, który minimalizuje skalarną funkcję kosztu. • Zdefiniowana jest ona przez odległość pomiędzy wektorem stanu x a wektorem pierwszego przybliżenia xb mnożoną przez wagę będąca odwrotnością kowariancji błędu i odległość pomiędzy wektorem stanu x, a wektorem obserwacji yo mnożoną przez odwrotność kowariancji błędów obserwacyjnych. • Zarówno metoda 3 D-Var jak i OI nie uwzględnia dynamiki modelu. • W metodzie OI minimalizacji dokonujemy w przestrzeni wektora obserwacji. • W metodzie 3 D-Var minimalizacji dokonujemy w przestrzeni wektora stanu. 2

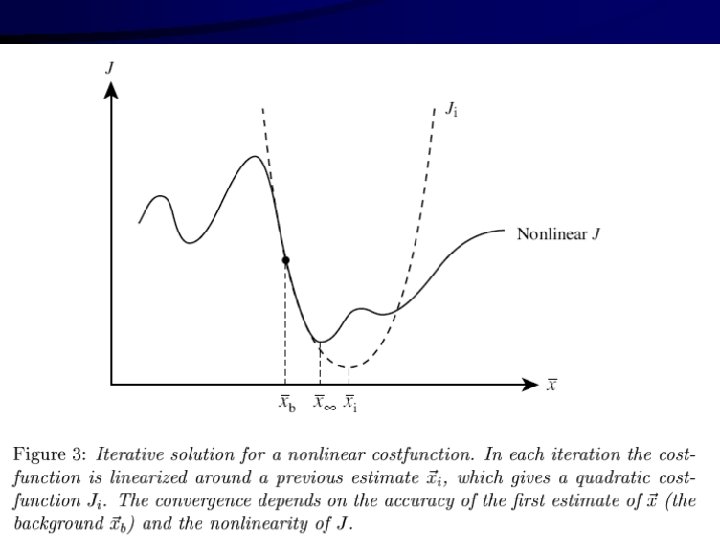
3 -wymiarowa analiza wariacyjna : 3 D-VAR • Rozważamy funkcję koszu oraz jej gradient w postaci: Minimalizacja wariacyjnej funkcji kosztu (na podstawie 2 wymiarowego modelu). Kwadratura funkcji kosztu ma kształt paraboloidy (w tym przypadku) z wartością minimalna dla optymalnej wartości analizy xa. Algorytm poszukiwania wartości minimalnej sprowadza się do poruszania po krzywej funkcji kosztu w kierunku największego gradientu funkcji. 3

• W praktyce punkt startowy minimalizacji zwany pierwszym przybliżeniem (first guess) jest często wybierany na podstawie informacji a priori (background) xb. • Nie jest to wybór obowiązkowy jednak należy pamiętać o różnicy pomiędzy informacją a priori, która jest używana w definicji funkcji kosztu od pierwszego przybliżenia, które jest używane do inicjalizacji procedury minimalizacyjnej. • Jeśli minimalizacja jest zadowalająca to wynik analizy nie zależy istotnie od wyboru wartości startowej. Jednak zawsze zależy od informacji a priori. • Znaczącym problemem analizy 3 D-Var jest konieczność znalezienia metody pozwalającej wyznaczyć macierz kowariancji B, która określa błędy informacji a priori dla każdej pary zmiennych modelu. • W większości przypadków macierz kowariancji błędu związana z obserwacjami jest przekątna macierzą blokową lub diagonalą. 4

• Łatwo zauważyć, że przekątna macierz blokowa implikuje, iż funkcja kosztu Jo jest sumą N skalarnych funkcji kosztu Jo, i każdej zdefiniowanej dla podmacierzy Ri oraz odpowiadającej Hi oraz yi. • Rozbicie funkcji kosztu Jo staje się użytecznym narzędziem do badania zachowania metody 3 D-Var ze względu na każdą obserwację (jej wartość i dopasowanie do wektora stanu x) • Dodatkowo pozwala to na wymuszenie słabszych więzów (ograniczeń) przez dodanie dodatkowego czynnika w funkcji kosztu Jc. • Prowadzi to jednak do warunku wstępnego co utrudnia i komplikuje minimalizację. 5

6

Przykłady Mając dany wektor obserwacyjny szacujemy wektor stanu xa. 7

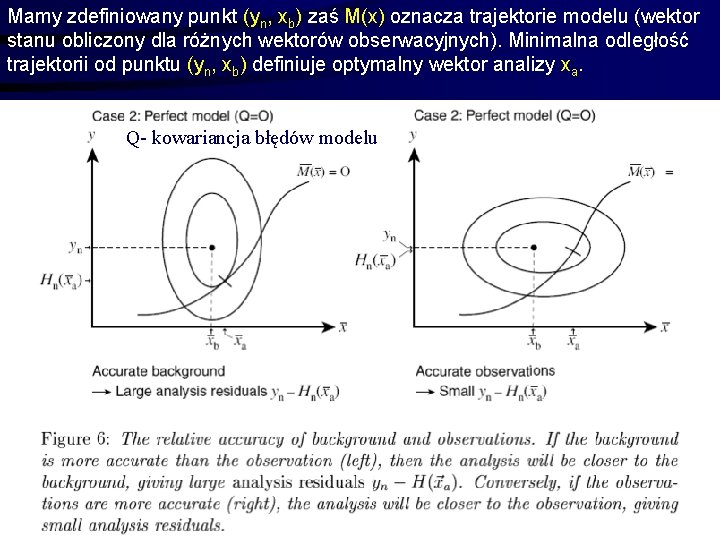
Mamy zdefiniowany punkt (yn, xb) zaś M(x) oznacza trajektorie modelu (wektor stanu obliczony dla różnych wektorów obserwacyjnych). Minimalna odległość trajektorii od punktu (yn, xb) definiuje optymalny wektor analizy xa. Q- kowariancja błędów modelu 8

9

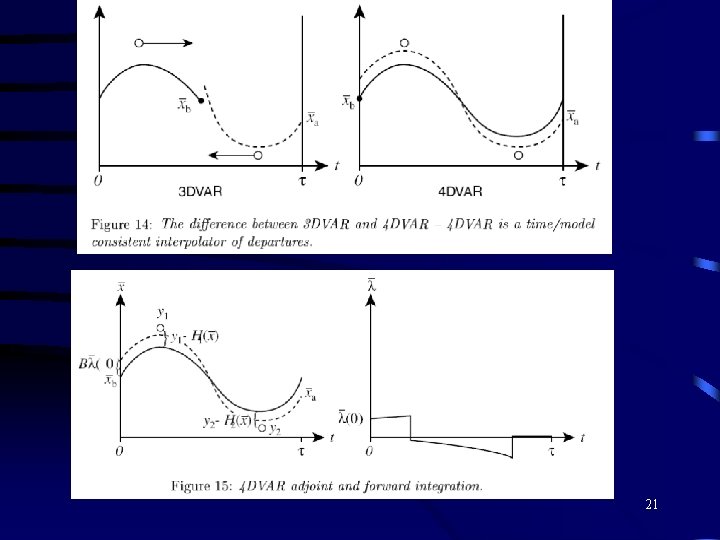
4 -wymiarowa analiza wariacyjna : 4 D-VAR • 4 D metoda jest uogólnieniem metody 3 D-Var poprzez uzależnienie obserwacji od czasu. • Równania pozostają takie same, jednak operator obserwacji jest uogólniony aby uwzględniać wyniki prognostyczne modelu. Dzięki czemu możemy porównywać wektor stanu modelu z obserwacjami dla określonego czasu. • Dla danego przedziału czasu analiza startuje w chwili początkowej, zaś obserwacje zdefiniowane są dla n okresów obserwacyjnych w badanych przedziale czasu. Indeks i będzie służył do oznaczania chwili czasu. • yj, xi oraz xti są obserwacjami, wektorem stanu oraz rzeczywistym wektorem stanu dla chwili czasu i, zaś macierz Ri jest macierzą kowariancji błędu dla obserwacji (yi-Hi(xti)) 10

• Operator obserwacji Hi w chwili czasu i jest linearyzowany do postaci Hi. • Macierz kowariancji B błędu informacji a priori jest zdefiniowany tylko dla czasu początkowego, podobnie wektor xb. • W tym przypadku postać funkcji kosztu jest następująca: lub 11

Analiza 4 D-Var • Definiujemy operator prognostyczny modelu M 0 i Opisuje on wektor stanu w chwili t=i obliczony na podstawie modelu prognostycznego startującego w chwili początkowej t=0. Ogólny problem metody 4 D-Var jest bardzo trudny do rozwiązania. Związku z czym stosuje się dwie hipotezy, które upraszczają problem: (1) Model prognostyczny może być wyrażony jako iloczyn pośrednich kroków prognostycznych. Jeśli przez Mi oznaczymy operator pomiędzy wektorem stanu w chwili i-1 oraz i (xi=Mixi-1) to wówczas możemy zapisać: 12

(2) Funkcja kosztu staje się kwadratowa gdy dokonamy linearyzacji operatora H oraz M podobnie zakładaliśmy w 3 D-Var gdzie M 0 i jest operatorem stycznym (pochodna operatora M) Powyższe hipotezy upraszczają problem minimalizacyjny do zagadnienia kwadratowego, które jest łatwiejsze do rozwiązania. Pierwszy czynnik funkcji kosztu Jb jest identyczny jak w metodzie 3 D-Var. Obliczenie natomiast drugiego członu Jo , wymaga n krotnego użycia modelu i całkowania równania modelu od chwili t=0 do t=i. W celu obliczenia gradientu funkcji kosztu musimy użyć model prognostyczny jeszcze więcej razy. W tym celu używania się pojęcia operatora sprzężonego oraz modelu sprzężonego (adjoint model). 13

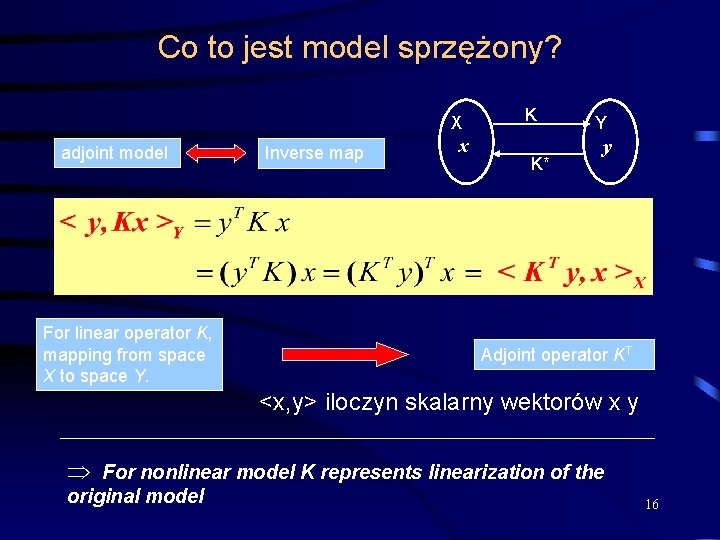
Operator sprzężony Niech <u, v> będzie iloczynem skalarnym, zaś K liniowym operatorem. Wówczas operator sprzężony zdefiniowany jest jako: Jeśli K jest operatorem rzeczywistym to wówczas K*=KT. Jeśli K jest operatorem zespolonym to K* =K+ Analiza czułości modelu na warunki początkowe Model F(x)=y Jak zaburzenie x wpływa na zaburzenie y Jak zaburzenie y wpływa na zaburzenie x 14

• Operator styczny K • Sprzężony operator styczny KT jest sprzężonym operatorem stycznym (adjoint tangentlinear model) Modele sprzężone używane są: w procedurach asymilacji danych przy badaniu czułości modeli na warunki początkowe 15

Co to jest model sprzężony? X adjoint model For linear operator K, mapping from space X to space Y. Inverse map x K K* Y y Adjoint operator KT <x, y> iloczyn skalarny wektorów x y Þ For nonlinear model K represents linearization of the original model 16

Minimalizacja 4 D-Var funkcji kosztu (1) Wykonujemy całkowanie równań modelu od wektora stanu x do xn dla każdej pory obserwacyjnej i (2) Obliczamy znormalizowane odchylenie modelu (3) Obliczamy wkład do funkcji kosztu (4) Wyznaczamy postać funkcji kosztu Obliczenie gradientu funkcji kosztu wymaga faktoryzacji 17

(5) Inicjalizujemy zmienną sprzężoną dla czasu końcowego (6) Dla każdego kroku czasu i-1 zmienna jest wyznaczana poprzez tak zwane wymuszenie sprzężone do oraz wykonanie całowania co jest równoznaczne z mnożeniem przez Mi. T (7) Ostatecznie w wyniku rekurencji otrzymujemy wartość zmiennej sprzężonej: Tak więc dokonujemy całkowania wstecznego (w czasie) modelu sprzężonego z krokiem czasu zdefiniowanego przez operator Mi. T oraz wymuszenie Hi. Tdi, które zależy od odległości pomiędzy trajektorią modelu i obserwacjami. 18

19

Uwagi • Metoda 4 D-Var działa jedynie gdy model jest idealny. W przypadku dużych błędów modelu metoda 3 D-Var mamy do czynienia z szeregiem problemów. • Metoda wymaga implementacji modelu sprzężonego, która jest bardzo pracochłonna dla skomplikowanych modeli prognoz pogody. 20

21

22

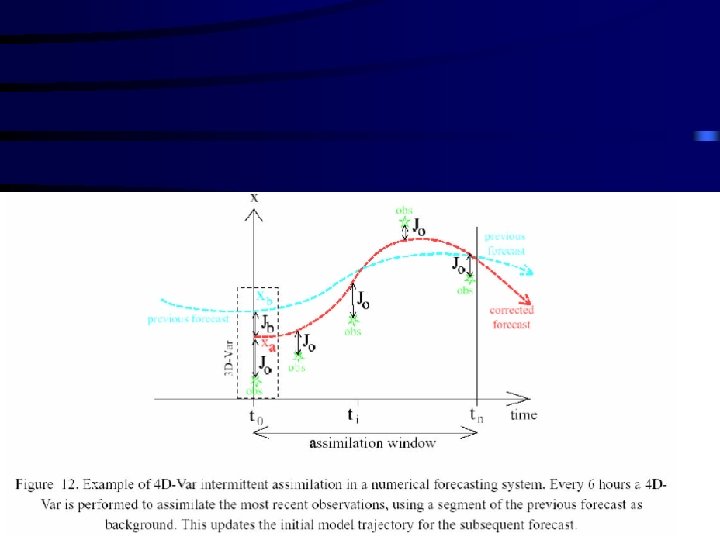
Rozważmy problem 3 godzinnej prognozy pogody (czerwona linia), która została użyta do pierwszego przybliżenia. Różnica pomiędzy obserwacjami a prognozą dla czasu T=0 jest niezerowa ze względu na: – Błędy modelu – Błędy obserwacji Trudno je jednak rozdzielić. 23

W metodzie wariacyjnej asymilacji danych próbujemy dopasować obserwacje do modelu w ten sposób, iż warunek początkowy uzyskany w ten sposób jest optymalne z punktu widzenia następnej prognozy. Na diagramie widoczne jest pierwsze przybliżenie w punkcie A. Pomimo, że jest ono zgodne z obserwacjami (T 3) prowadzi do znacznego błędu prognozy (T=0). Odcieniem zielonym zaznaczono obserwacje (z błędem). 24

Wśród metod 4 D-Var wyróżniany metodę sprzężoną (adjoint method) W metodzie tej używa się kolejnych iteracji do uzyskania optymalnej prognozy Innymi słowy analiza Aadj prowadzi to ustawienia trajektorii modelu (linia niebieska) w taki sposób, iż uzyskujemy lepszą 3 godzinną prognozę chociaż dla czasu T-3 może ona znaczącą odbiegać od obserwacji. W pewnym więc sensie wykorzystujemy informację o błędzie prognozy pogody przy zadanych warunkach początkowych. Dzięki analizie Aadj zmniejszamy ten błąd. 25

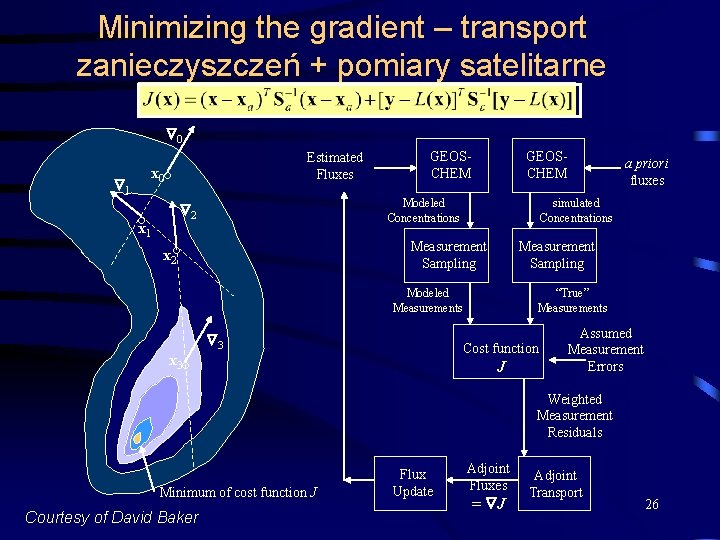
Minimizing the gradient – transport zanieczyszczeń + pomiary satelitarne 0 1 Estimated Fluxes x 0 ° °x 1 GEOSCHEM Modeled Concentrations 2 simulated Concentrations Measurement Sampling x 2° Measurement Sampling Modeled Measurements x 3 3 “True” Measurements Cost function ° a priori fluxes J Assumed Measurement Errors Weighted Measurement Residuals Minimum of cost function J Courtesy of David Baker Flux Update Adjoint Fluxes = J Adjoint Transport 26

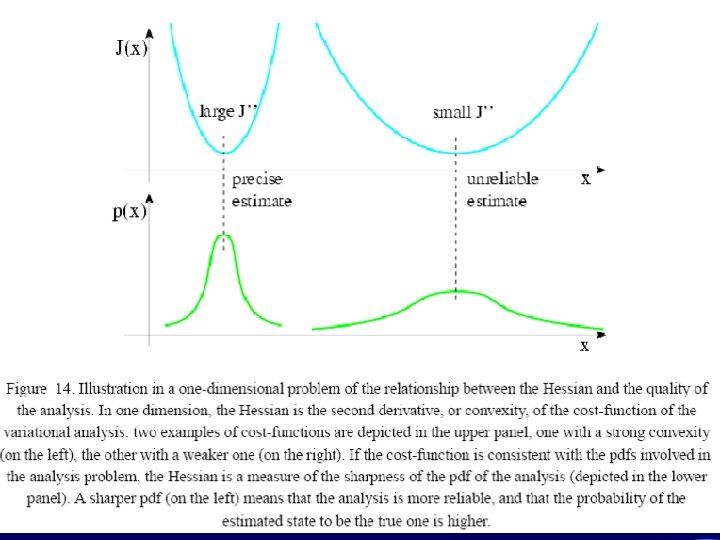
Szacowanie błędów analizy • W przypadku metody OI macierz kowariancji błędu analizy dana jest wzorem lub redukuje się do postaci W przypadku metod wariacyjnych macierz kowariancji błędu analizy wyznaczana jest z drugiej pochodnej funkcji kosztu 27

28
 Yves markowicz
Yves markowicz Bezprawne niszczenie informacji
Bezprawne niszczenie informacji Repozytorium informacji turystycznej
Repozytorium informacji turystycznej Wyszukiwanie informacji turystycznych
Wyszukiwanie informacji turystycznych Informacja zwrotna przykłady
Informacja zwrotna przykłady Analiza dokumentacji
Analiza dokumentacji Cigw
Cigw Administrator bezpieczeństwa informacji szkolenie
Administrator bezpieczeństwa informacji szkolenie Wyszukiwanie informacji w internecie ćwiczenia
Wyszukiwanie informacji w internecie ćwiczenia 09102000 colour
09102000 colour Krzywa podaży lucasa
Krzywa podaży lucasa Geoprtal
Geoprtal Techniki zbierania informacji
Techniki zbierania informacji Wielkości wprost proporcjonalne i odwrotnie proporcjonalne
Wielkości wprost proporcjonalne i odwrotnie proporcjonalne Cechy dobrej prezentacji
Cechy dobrej prezentacji Internet jako ocean informacji
Internet jako ocean informacji Postulat postarzania informacji
Postulat postarzania informacji Instytut elektroenergetyki pł
Instytut elektroenergetyki pł Instytut studiów podyplomowych częstochowa
Instytut studiów podyplomowych częstochowa Passato prossimo regolare
Passato prossimo regolare Instytut geofizyki uw
Instytut geofizyki uw Most typu maryland
Most typu maryland Instytut informatyki uwr
Instytut informatyki uwr Instytut na rzecz ekorozwoju
Instytut na rzecz ekorozwoju Instytut maszyn przepływowych
Instytut maszyn przepływowych Instytut biochemii i biofizyki pan
Instytut biochemii i biofizyki pan Socjologia grup dyspozycyjnych
Socjologia grup dyspozycyjnych Instytut technologii eksploatacji radom
Instytut technologii eksploatacji radom Instytut rozwoju wsi i rolnictwa pan
Instytut rozwoju wsi i rolnictwa pan