Analisis Algoritma Modul 4 Analisis Algoritma Struktur Data

Analisis Algoritma Modul 4 : Analisis Algoritma & Struktur Data

Analisis Algoritma � ilmu yang digunakan untuk mengetahui ukuran “kerumitan” (complexity) dari suatu algoritma sehingga dapat diketahui apakah suatu algoritma cukup efisien bila diimplementasi-kan. � Suatu ukuran kerumitan yang sering digunakan adalah asymptotic time complexity, kerumitan waktu asimptotik, suatu ukuran yang menunjukkan perkembangan waktu proses sesuai dengan pertambahan jumlah data input.

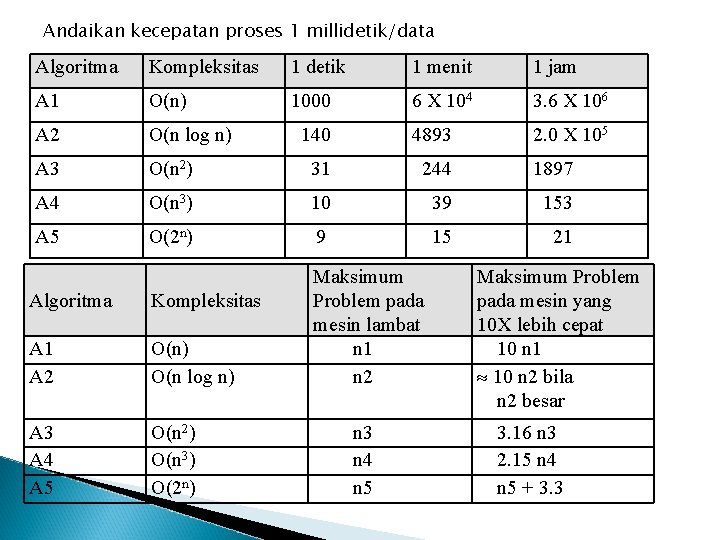
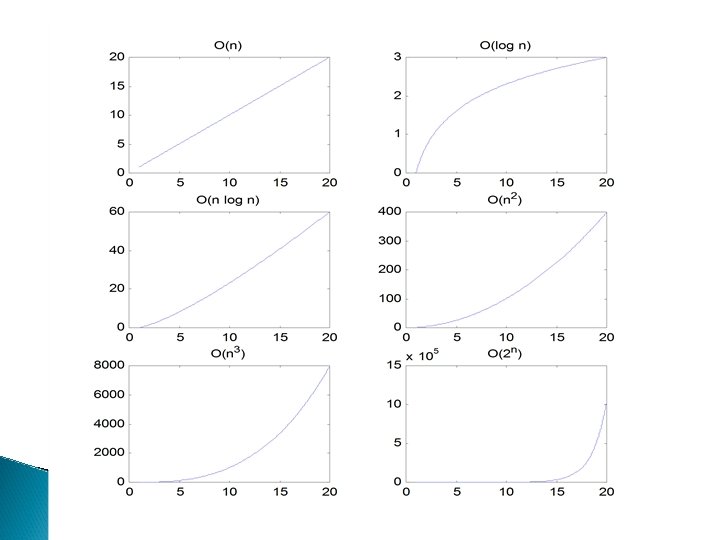
� andaikan suatu algoritma memerlukan waktu yang berbanding dengan kuadrat dari jumlah data, T=O(n 2), apabila satu data diproses 1 detik, berarti 10 data memerlukan 100 detik. � Peningkatan kecepatan prosessor tidak terlalu menolong apabila algoritma-nya terlalu kompleks � Berikut ini adalah tabel perbandingan antara lima macam kerumitan algoritma

Andaikan kecepatan proses 1 millidetik/data Algoritma Kompleksitas 1 detik 1 menit 1 jam A 1 O(n) 1000 6 X 104 3. 6 X 106 A 2 O(n log n) 140 4893 2. 0 X 105 A 3 O(n 2) 31 244 1897 A 4 O(n 3) 10 39 153 A 5 O(2 n) 9 15 21 Algoritma Kompleksitas A 1 A 2 O(n) O(n log n) A 3 A 4 A 5 O(n 2) O(n 3) O(2 n) Maksimum Problem pada mesin lambat n 1 n 2 n 3 n 4 n 5 Maksimum Problem pada mesin yang 10 X lebih cepat 10 n 1 10 n 2 bila n 2 besar 3. 16 n 3 2. 15 n 4 n 5 + 3. 3

Algoritma Insertion_Sort � { melakukan pengurutan data dengan teknik penyisipan } � � Defenisi Variabel � int i, j, n = 100; � int A[n], key; � � Rincian Langkah: � for j = 2 to n � key A[j]; � { Sisip(A[j]) kedalam deretan A[1. . j-1] } � i (j – 1) ; � while (i > 0 and A[i] > key) � A[i+1] A[i]; � i i – 1; � endwhile � A[i+1] key; � endfor. �

Perhitungan Biaya: � baris instruksi biaya � � 1. for j = 2 to n b 1 � 2. key A[j]; b 2 � { Sisip(A[j]) kedalam deretan A[1. . j-1] } � 3. i (j – 1) ; b 3 � 4. while (i > 0 and A[i] > key) b 4 � 5. A[i+1] A[i]; b 5 � 6. i i – 1; b 6 � endwhile � 7. A[i+1] key; b 7 � endfor. � waktu n n-1 j (j – 1) n-1 Total Biaya: T(n) = b 1. n + b 2. (n-1) + b 3. (n-1) + b 4. j + b 5. (j-1) + b 6. (j-1) + b 7. (n-1) Dimana : j = sigma dari j=2 s/d n, hasilnya adalah: n(n+1)/2 – 1 (j – 1) utk j=2 s/d n adalah : n(n-1)/2

� dengan � T(n) demikian: = b 1. n + b 2. (n-1) + b 3. (n-1) + b 4. (n(n+1)/2 – 1) + b 5. (n(n-1)/2) + b 6. (n(n 1)/2) + b 7. (n-1) � T(n) = (b 4/2 + b 5/2 + b 6/2) n 2 + (b 1 + b 2 + b 3 + b 4/2 – b 5/2 – b 6/2 + b 7) n – (b 2 + b 3 + b 4 + b 7). � Atau T(n) = A n 2 + B n + C T(n) = O(n 2)

� Sebagai kesimpulan, berikut ini disajikan salah satu langkah dalam melakukan analisis algoritma secara eksak: � 1. Tuliskan algoritma secara lengkap 2. Tentukan waktu untuk setiap instruksi dasar 3. Tentukan biaya atau frekuensi masing-masing instruksi dasar 4. Hitung total running-time dengan menjumlahkan perkalian biaya dan waktu dari setiap baris instruksi dasar 5. Kumpulkan suku yang memiliki order yang sama 6. Lakukan pendekatan upper-bound

Analisis Algoritma Euclid adalah algoritma untuk menghitung GCD (Greatest Common Divisor) atau KPT (Kelipatan Pembagi Terbesar), yang disajikan dalam bentuk fungsi sbb: � Fungsi Euclid(m, n) integer { menghitung KPT dari bilangan m dan n } Defenisi Variabel: int t; Rincian Langkah: while (m > 0) do t n mod m; n m; m t; endwhile; return n �

� Andaikan n > m, misalnya n=24 dan m=18 � k=1 t = 24 mod 18 = 6, n=18, m=6 � k=2 t = 18 mod 6 = 0, n=6, m=0 � m=0 2 putaran, dengan KPT=n=6 � K < log(18)=2. 89 � Andaikan n=124 dan m=28 � K=1 t=124 mod 28 = 12, n=28, m=12 � K=2 t = 28 mod 12 = 4, n=12, m=4 � K=3 t = 12 mod 4 = 0, n=4, m=0 � M=0 3 putaran, dengan KPT = 4 � K < log(28) = 3. 33

� Andaikan k adalah jumlah putaran dalam while, dan pada saat putaran ke-i berlangsung diperoleh ni = mi-1 dan mi = ni-1 mod mi-1 dimana ni > mi mi = ni-1 mod mi-1 < ni-1/2 = mi-2/2 � Bila k dianggap ganjil = 2 d + 1 maka: mk-1<mk-3/2<mk-5/4<…<m 0/2 d � Karena mk-1 1 maka m 0>2 d atau d <2 log m 0 � Maka k = 2 d + 1 1 + 2 log m 0 � Jadi T(n) = O(log m)

Tower of Hanoi � “The Tower of Hanoi”. Menurut legenda dibalik soal ini, pada suatu waktu menurut kepercayaan Budha, Tuhan meletakkan 64 piringan emas (yang tengahnya berlubang) dengan ukuran yang berbeda pada sebuah tonggak yang dipenuhi berlian, dimana piringan tersusun menurut ukurannya, piringan terbesar berada paling bawah dan piringan terkecil paling atas, sehingga berbentuk menara (tower). Disediakan pula dua tonggak yang lain di-sekitarnya. Para pendeta Budha diperintahkan untuk memindahkan semua piringan ini dari satu tonggak ke tonggak lain, dengan syarat harus tersusun kembali seperti menara. Tonggak yang satu-nya lagi dapat digunakan untuk menyimpan sementara piringan yang akan dipindah namun harus tetap mengikuti urutan diameter, yang lebih besar dibawah, yang lebih kecil diatas. Andaikan pendeta Budha mampu memindahkan satu piringan setiap detik berapa lama waktu yang diperlukan untuk memindahkan ke-64 piringan emas ini dari satu tonggak ke tonggak lain dalam keadaan tersusun sempurna? Para pendeta Budha konon mempercayai bahwa pada saat semua piringan ini bisa pindah dengan sempurna maka pada saat itu “kiamat” datang! Adakah diantara anda yang bisa menjawab, berapa tahun diperlukan untuk melakukan pekerjaan tersebut?

Prosedur Hanoi(m, a, c, b) { memindahkan m cincin dari tongkat a ke tongkat c } Defenisi Variabel: int m; char a, b, c; Rincian langkah: if (m==1) then write(“pindah dari “, a, “ke “, c); else Hanoi(m-1, a, b, c); write(“pindah dari “, a, “ke”, c); Hanoi(m-1, b, c, a); endif A B C

� � Soal ini dapat diselesaikan dengan logika matematik, menggunakan “induksi” dan “rekurensi”. Strateginya sebagai berikut: Bila tidak ada piringan (n=0) maka tidak ada yang perlu dipindahkan T(0) = 0. Bila ada 1 piringan (n=1) maka hanya perlu 1 langkah, T(1)=1 Bila ada 2 piringan (n=2) maka perlu 3 langkah, atau T(2)=3, yaitu: ◦ pindahkan piring atas dari A ke B ◦ pindahkan piring bawah dari A ke C ◦ pindahkan piring atas dari B ke C � Bila ada 3 piringan (n=3) maka perlu 7 langkah, atau T(3)=7, yaitu: ◦ pindahkan dua (n-1) piring atas: �paling atas dari A ke C �yang tengah dari A ke B �kembalikan paling atas dari C ke B ◦ pindahkan piring paling bawah ke C ◦ pindahkan dua (n-1) piring dari B ke C �paling atas dari B ke A dulu �yang tengah dari B ke C �paling atas dari A ke C � T(n) = T(n-1) + 1 + T(n-1) = 2 T(n-1) + 1

� Gunakan Rekurensi tak homogen: atau T(n) – 2 T(n-1) = 1 karakteristik : T(n)- 2 T(n-1)=1. 1 b=1, P(n)=1, d=0 atau (x – 2)(x-1) = 0 shg T(n) = c 1. 1 + c 2. 2 n atau T(n)=O(2 n) Bila n=64, T(n) 264 1. 84 x 1019 Bila unit waktu pemindahan 1 detik maka T(n) = 1. 84 x 1019 / (60 x 24 x 356) thn = 5. 99 x 1011 tahun = 599 milyar tahun

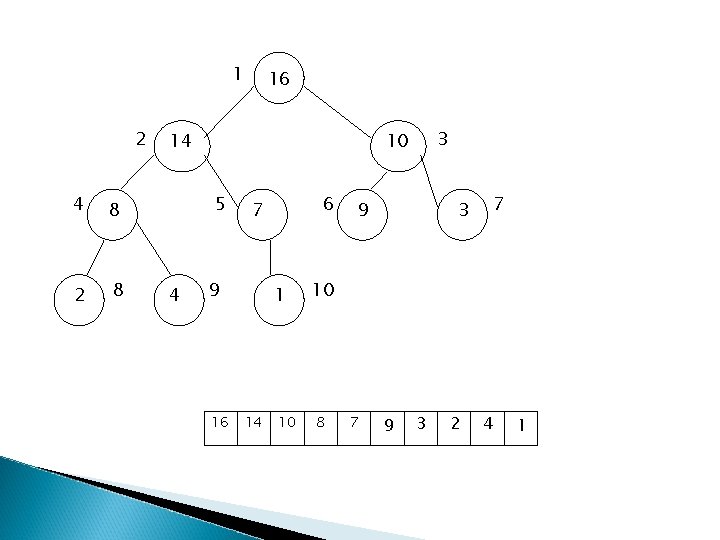
Binary Heap � Binary Heap adalah suatu struktur data yang dapat diwakili oleh suatu larik (array), juga dapat divisualisasi sebagai pohon biner, misalnya pada gambar berikut ini: � Sifat utama dari suatu “heap” adalah isi suatu node harus lebih besar (paling tidak sama) dari isi kedua node dibawahnya: �A[parent(i)] A[i] �parent(i) floor(i/2) �left(i) 2 i �right(i) 2 i + 1

1 2 4 8 2 8 16 14 5 4 3 10 9 16 6 7 14 1 10 10 8 9 7 7 3 9 3 2 4 1

� Prosedur Build_Heap(A) � { membentuk binary heap dari array A } � Definisi Variabel � int A[n]; � int i; � Rincian Langkah � size_heap[A] lenght[A]; � for i floor(length[A]/2) downto 1 � do Heapify(A, i); �

� Prosedur Heapify(A, i) � { mengatur elemen agar memenuhi sifat Heap } � Definisi Variabel � int largest, L, R; � Rincian Langkah � L left(i); � R right(i); � if (L size_heap[A] and A[L] > A[i]) � then largest L; � else largest i; � if (R size_heap[A] and A[R] > A[largest]) � then largest R; � if (largest i) � then Tukar(A[i], A[largest]); � Heapify(A, largest);

� Analisis algoritma diatas adalah sbb: � Prosedur Build_Heap(A), pada prinsipnya memanggil prosedur Heapify(A, i) sebanyak (n/2) kali bila length[A] = n. � Prosedur Heapify(A, i), pada kondisi paling jelek, setiap cabang memiliki turunan maksimal 2 n/3, sehingga rekurensi-nya T(n) T(2 n/3) + (1) � Solusi rekurensi Heapify(A, i) adalah T(n) = O(lg n) � Dengan demikian kompleksitas prosedur membentuk binary heap adalah: n/2. O(lg n) O(n lg n).