AAE 666 Final Presentation Spacecraft Attitude Control Justin

AAE 666 Final Presentation Spacecraft Attitude Control Justin Smith Chieh-Min Ooi April 30, 2005

Problem Description n n The problem considered is that of designing an attitude regulator for rigid body (spacecraft) attitude regulation The closed-loop system must have exactly one equilibrium point, namely when the body and inertial coordinate systems coincide The feedback control law has to be chosen carefully to meet the above requirement of only possessing exactly one equilibrium state for the closed-loop system Equilibrium point must be asymptotically stable for arbitrary initial conditions, when there are no external disturbing torques acting on the body Compared results of a linear regulator and a non-linear regulator with a numerical example

Dynamics n n Two Cartesian coordinate sets chosen; inertially fixed and body-fixed Origin taken as mass center These assumptions allow for decoupling of rotational and translational dynamics Body principal moments of inertia are taken as the body-fixed axes

Euler’s Equations

Quaternions n n n Problems of singularity (gimbal lock) do not arise due to absence of trigonometric functions Any change in orientation can be expressed with a simple rotation The Euler symmetric parameters may be interpreted in terms of a rotation through an angle Φ about an axis defined by a unit vector e = [e 1 e 2 e 3]T via the relations q 0 = cos(Φ/2), qi = ei sin(Φ/2), i = 1, 2, 3

Quaternions (cont’d) n n The quaternion differential equations are The use of a four-parameter scheme rather than a threeparameter scheme results in redundancy of one of the quarternion parameters. This is evident as every solution of the differential equation above satisfies the constraint:

Control Inputs n n n Control torques applied to the three body axes Implemented with throttleable reaction jets or momentum exchange devices Must include the dynamical equations of the flywheel, introducing three new state variables 10 first-order, coupled, non-linear differential equations necessary to describe system State variables include spacecraft angular momentum components, quaternions, and flywheel angular momentum components

Equations of Motion n Define parameters to simplify equations:

Equations of Motion

Controller Design Criterion n n Devise a feedback control law relating three control torques to 10 state variables The closed-loop system must have exactly one equilibrium point Equilibrium point must be asymptotically stable for arbitrary initial conditions, when there are no external disturbing torques acting on the body Equilibrium State: h 1= h 2 = h 3 = 0; q 0 = 1; q 1 = q 2 = q 3 = 0

Equations of Motion

Globally Stable Non-Linear Spacecraft Attitude Regulator n An asymptotically stabilizing feedback regulator is defined by:

Design Parameters

Globally Stable Linear Spacecraft Attitude Regulator for i=1, 2, 3, where ki > 0, c > 0 are constant control gains

Lyapunov Proof of Stability n Candidate Lyapunov function for the linear regulator case: n Candidate Lyapunov function for the non-linear regulator case: n Global asymptotic stability (GAS) since V is positive definite and Vdot < 0, for all state variables ≠ 0

Simulation Parameters

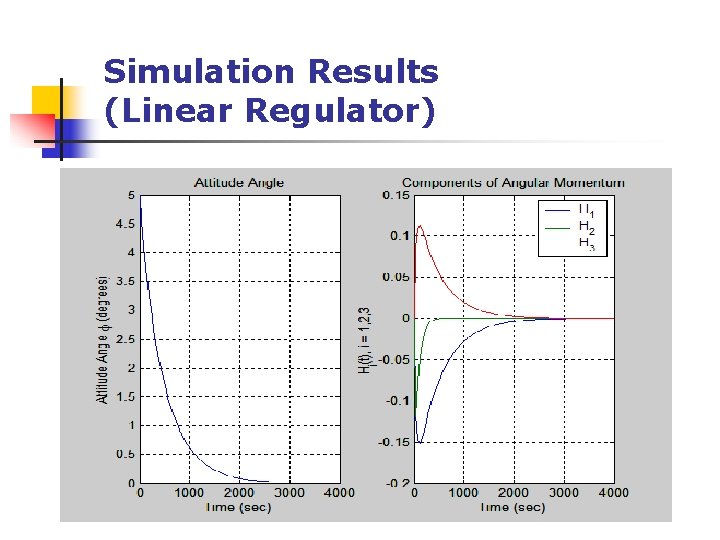
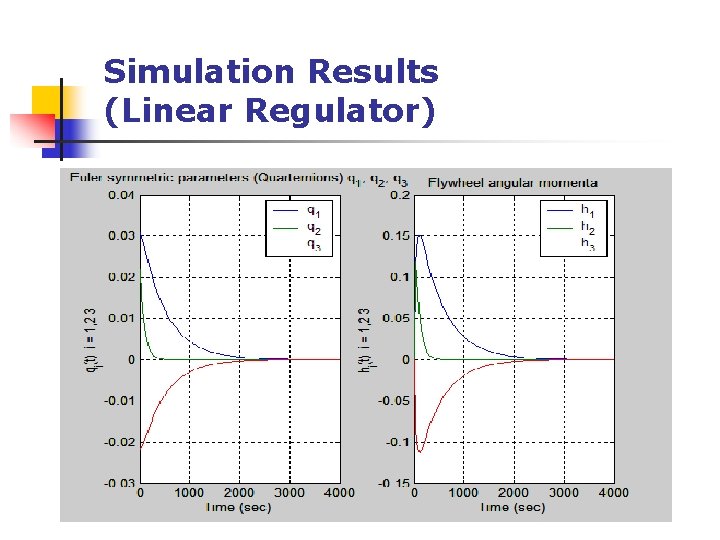
Simulation Results (Linear Regulator)

Simulation Results (Linear Regulator)

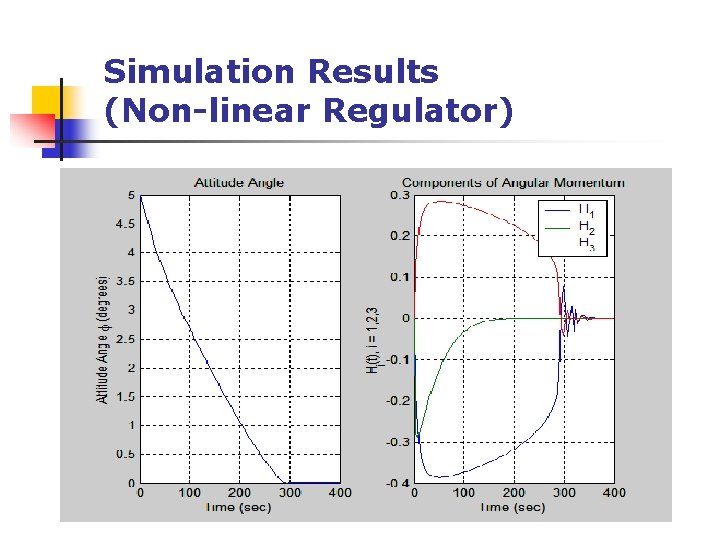
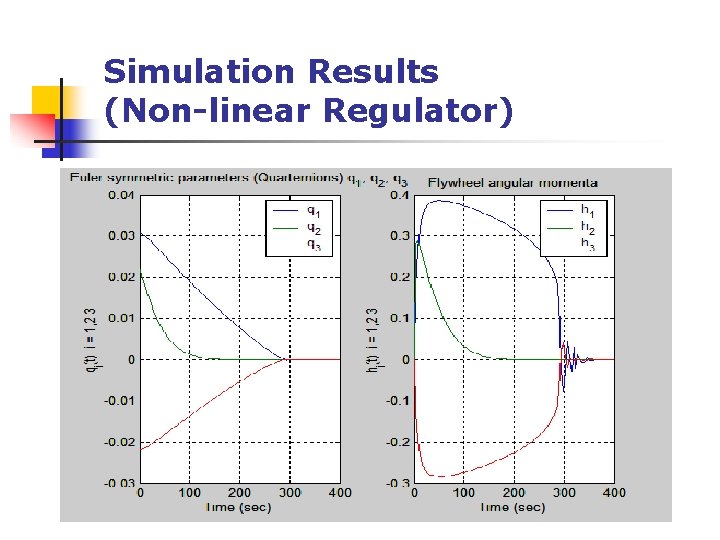
Simulation Results (Non-linear Regulator)

Simulation Results (Non-linear Regulator)

Analysis n n n An initial disturbance in the quaternion parameters causes a disturbance in the spacecraft’s angular momentum and flywheel angular momenta Flywheel angular momenta directly opposes the angular momentum of the spacecraft to bring it back to its initial attitude Attitude error, Φ(. ), regulates to zero for both linear and nonlinear cases Equilibrium is achieved much faster with the use of non-linear feedback regulators (approx 350 seconds for the non-linear case as compared to approx 3000 seconds for the linear case) The desired equilibrium state of h 1=h 2=h 3=0; q 0=1; q 1=q 2=q 3=0 was successfully achieved

Analysis (Cont’d) n n For both linear and non-linear cases, tweaking the gains affects how the system behaves From Vdot equation previously, it can be seen that large gains will improve stability of the linear regulator Larger gains result in spacecraft angular momentum and flywheel angular momenta achieving equilibrium conditions faster Same results could be observed by increasing the gains for the non-linear regulator

Conclusion n n n The rotational motion of an arbitrary rigid body (spacecraft) subject to control torques may be described by the EOMs defined earlier If linear feedback control law with constant coefficients is used, the closed-loop system is globally asymptotically stable (GAS) Lyapunov techniques were used to prove stability For the non-linear feedback regulator, if either pj > 1 or πj > 1 for some j, then a ‘higher-order’ feedback term is introduced in the control If pj Є (1/2, 1) or πj Є (1/2, 1) for some j, then a ‘lower-order’ feedback term is introduced Lower-order feedback exhibits efficient regulation characteristics near the equilibrium state

References n n n S. V. Salehi and E. P. Ryan; A non-linear feedback attitude regulator Richard E. Mortensen; A globally stable linear attitude regulator Professor K. C. Howell; AAE 440 notes

Questions? ? ?