9 4 Comparison of series Greg Kelly Hanford



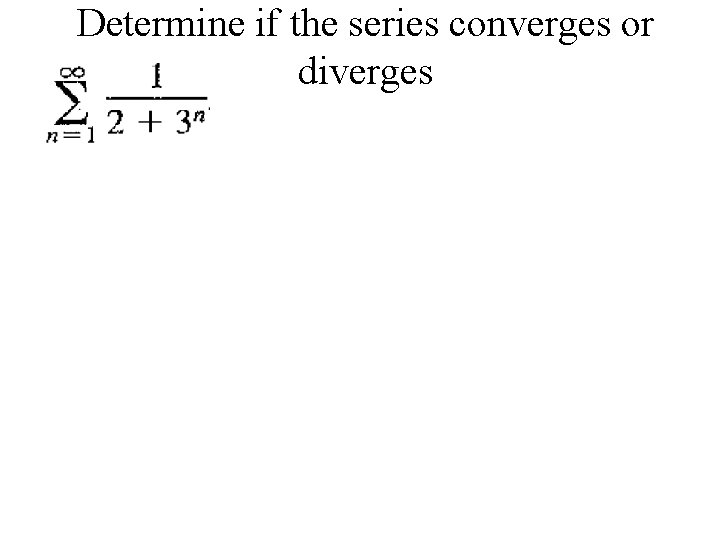

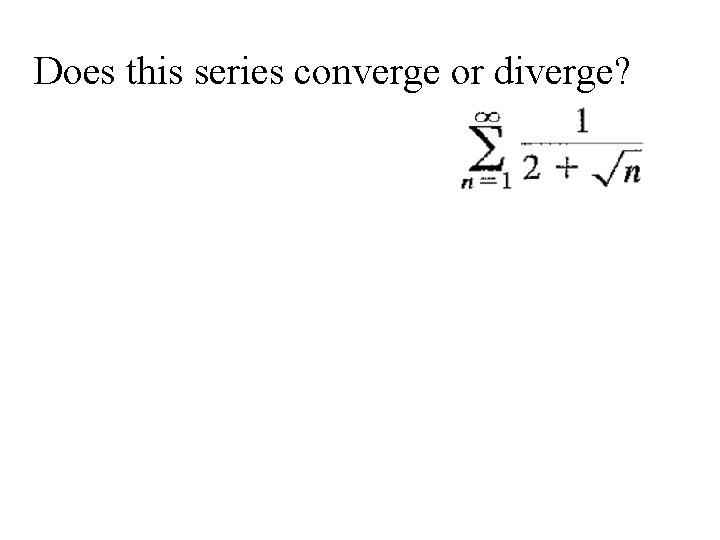








- Slides: 14

9. 4 Comparison of series Greg Kelly, Hanford High School, Richland, Washington

Convergence The series that are of the most interest to us are those that converge. Today we will consider the question: “Does this series converge, and if so, for what values of x does it converge? ”

Direct Comparison Test For non-negative series: If every term of a series is less than the corresponding term of a convergent series, then both series converge. If every term of a series is greater than the corresponding term of a divergent series, then both series diverge. This series converges. So this series must also converge. So this series must also diverge. This series diverges.
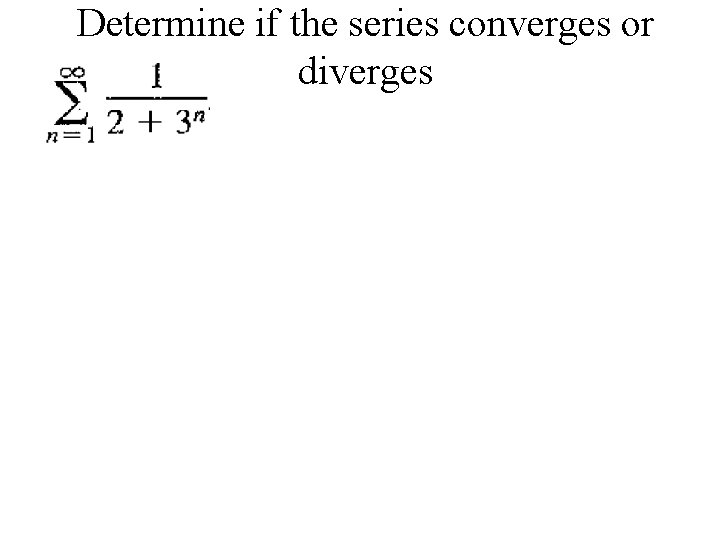
Determine if the series converges or diverges

Determine if the series converges or diverges This series very much resembles a special series: which is a Geometric series that converges Every term of our original series is positive and smaller (has a larger denominator) than the geometric series. This series must converge due to the direct comparison test.
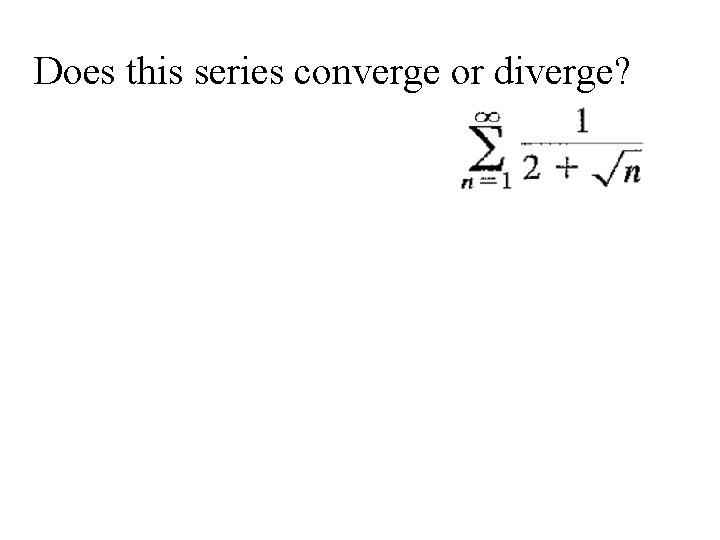
Does this series converge or diverge?

Does this series converge or diverge? This series resembles the divergent series: unfortunately, we can not use the direct Comparison test with this series because each term of this series is smaller than the one that we are looking at

Does this series converge or diverge? We will compare to Which is also a divergent P series Comparing terms we find that Therefore this series diverges

An Interesting Fact We will prove this fact later in the chapter. However, we will need this fact today in order to doing comparing.

Ex. 3: Prove that converges for all real x. There are no negative terms: larger denominator is the Taylor series for , which converges. The original series converges. The direct comparison test only works when the terms are non-negative.

Absolute Convergence If converges, then we say converges absolutely. The term “converges absolutely” means that the series formed the absolute value of each term If by taking converges, then converges. Sometimes in the English language we use the word “absolutely” to mean “really” or “actually”. This is If the series not the caseformed here! by taking the absolute value of each term converges, then the original series must also converge. “If a series converges absolutely, then it converges. ”

Ex. 4: We test for absolute convergence: Since , converges to converges by the direct comparison test. Since converges absolutely, it converges.

Homework p. 630 1 -14 all • Two mathematicians are studying a convergent series. The first one says: "Do you realize that the series converges even when all the terms are made positive? " The second one asks: "Are you sure? " "Absolutely!"

There are three possibilities for power series convergence. 1 The series converges over some finite interval: (the interval of convergence). There is a positive number R such that the series diverges for but converges for . The series may or may not converge at the endpoints of the interval. 2 The series converges for every x. ( 3 The series converges for at and diverges everywhere else. ( ) (As in the previous example. ) ) The number R is the radius of convergence.
 Greg kelly calculus
Greg kelly calculus Hanford
Hanford Hanford
Hanford Craig hanford
Craig hanford Project portfolio management hanford ibm
Project portfolio management hanford ibm Compairson test
Compairson test Comparison test
Comparison test Serie de taylor
Serie de taylor Series aiding and series opposing
Series aiding and series opposing Deret maclaurin
Deret maclaurin Arithmetic series vs geometric series
Arithmetic series vs geometric series Maclaurin series vs taylor series
Maclaurin series vs taylor series P series ibm
P series ibm Balmer series lyman series
Balmer series lyman series Shunt shunt feedback amplifier
Shunt shunt feedback amplifier