7 6 EXPONENTIAL FUNCTIONS Function Rule An equation

7. 6 EXPONENTIAL FUNCTIONS: Function Rule: An equation that describes a function. Exponent: A number that shows repeated multiplication.

GOAL:

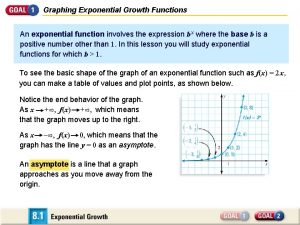
Definition: An EXPONENTIAL FUNCTION is a function of the form: Constant Base Exponent Where a ≠ 0, b > o, b ≠ 1, and x is a real number.

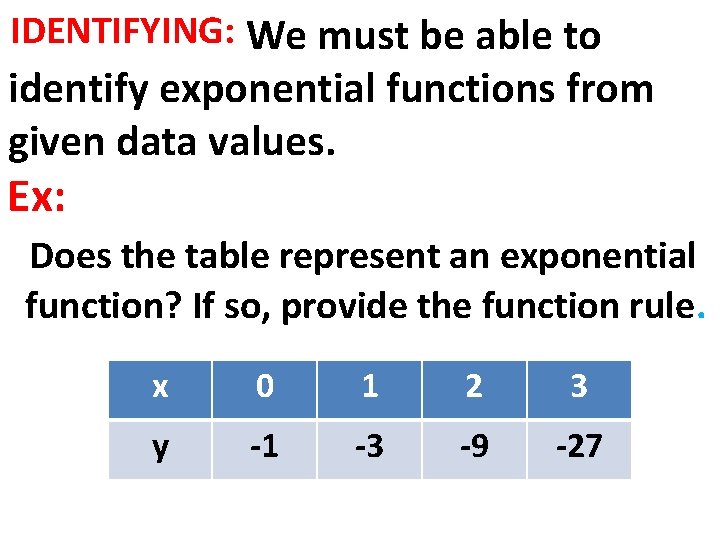
IDENTIFYING: We must be able to identify exponential functions from given data values. Ex: Does the table represent an exponential function? If so, provide the function rule. x 0 1 2 3 y -1 -3 -9 -27

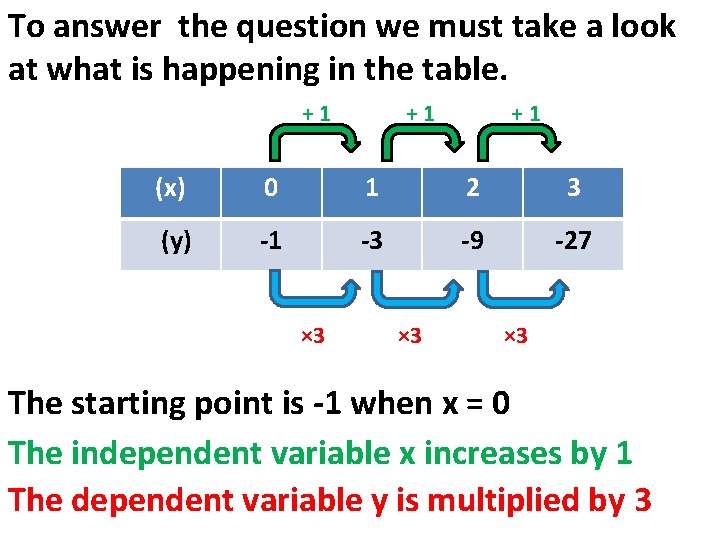
To answer the question we must take a look at what is happening in the table. +1 +1 +1 (x) 0 1 2 3 (y) -1 -3 -9 -27 × 3 × 3 The starting point is -1 when x = 0 The independent variable x increases by 1 The dependent variable y is multiplied by 3

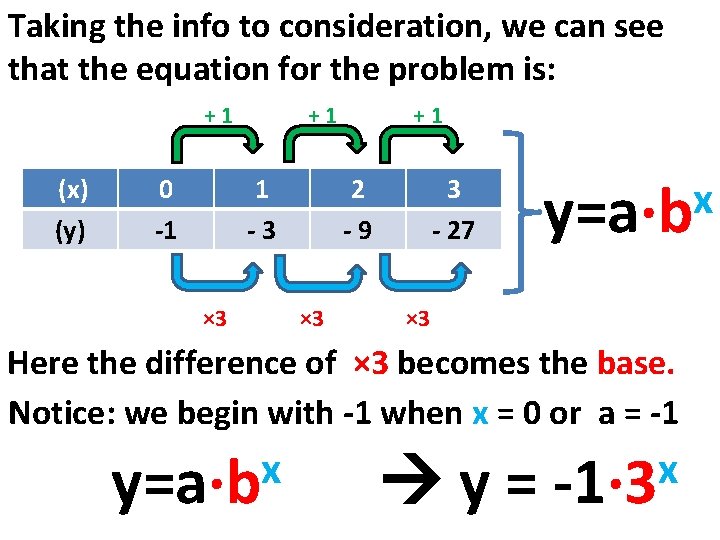
Taking the info to consideration, we can see that the equation for the problem is: +1 (x) (y) 0 -1 +1 1 -3 × 3 +1 2 -9 × 3 3 - 27 x y=a∙b × 3 Here the difference of × 3 becomes the base. Notice: we begin with -1 when x = 0 or a = -1 x y=a∙b y= x -1∙ 3

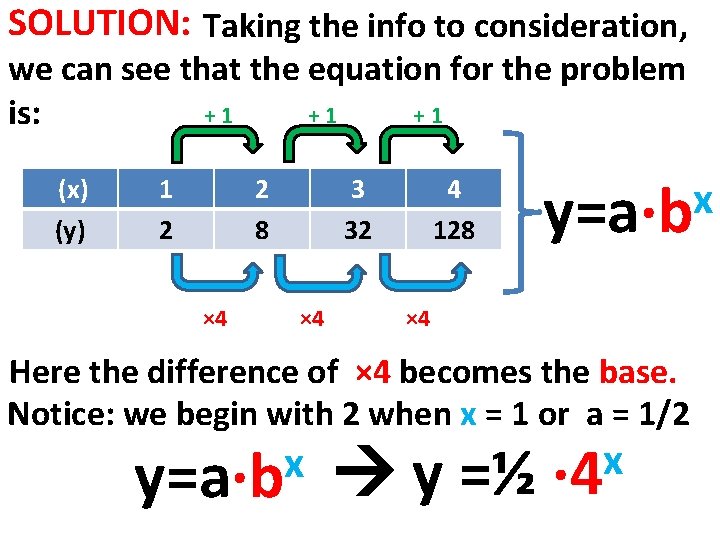
YOU TRY IT: Does the table represent an exponential function? If so, provide the function rule. x 1 2 3 4 y 2 8 32 128

SOLUTION: Taking the info to consideration, we can see that the equation for the problem +1 +1 +1 is: (x) (y) 1 2 2 8 × 4 3 32 × 4 4 128 x y=a∙b × 4 Here the difference of × 4 becomes the base. Notice: we begin with 2 when x = 1 or a = 1/2 x y=a∙b y =½ x ∙ 4

Summary: Linear Functions: y = mx + b The difference in the independent variable (y) is in form of addition or subtraction. Exponential Equations: y = abx The difference in the independent variable (y) is multiplication

EVALUATING: We must be able to evaluate exponential functions. Ex: An investment of $5000 doubles in value every decade. Write a function and provide the worth of the investment after 30 years.

EVALUATING: To provide the solution we must know the following formula: A= x P∙ 2 A = total P = Principal (starting amount) 2 = doubles x = time

SOLUTION: An investment of $5000 doubles in value every decade. Write a function and provide the worth of the investment after 30 years. Amount: unknown Principal: $5000 Doubles: 2 Time (x): 30 yrs (3 decades) x P∙ 2 A= 3 A = 5000∙ 2 A = 5000∙(8) A = 40, 000

YOU TRY IT: Suppose 30 flour beetles are left undisturbed in a warehouse bin. The beetle population doubles each week. Provide a function and the population after 56 days.

SOLUTION: Suppose 30 flour beetles are left undisturbed in a warehouse bin. The beetle population doubles each week. Provide a function and the population after 56 days. Amount: unknown Principal: 30 Doubles: 2 Time (x): 56 days (8 weeks) x P∙ 2 A= 8 A = 30∙ 2 A = 30∙(256) A = 7, 680

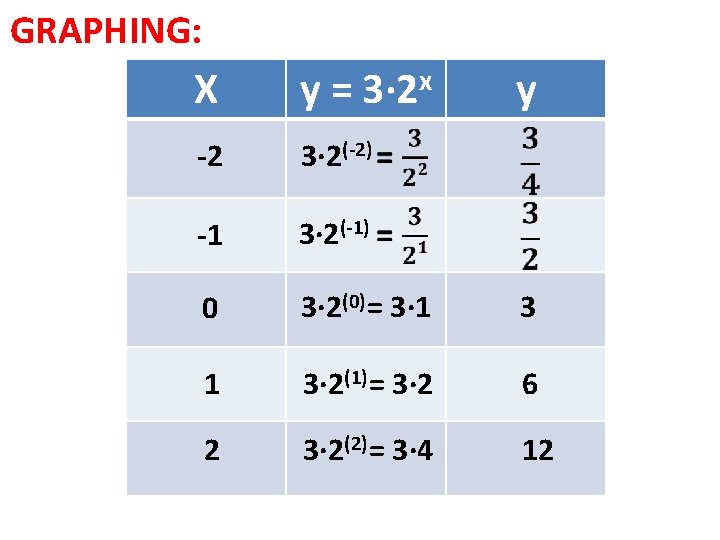
GRAPHING: To provide the graph of the equation we can go back to basics and create a table. Ex: What is the graph of y = 3∙ 2 x?

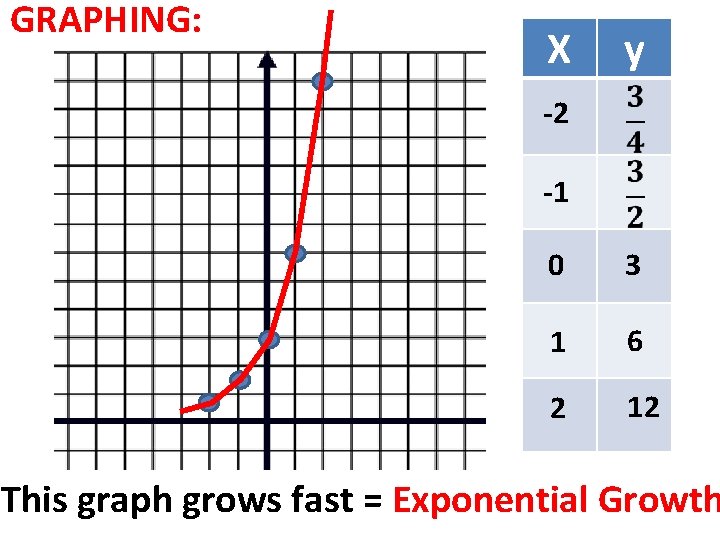
GRAPHING: X y = 3∙ 2 x y -2 3∙ 2(-2) -1 3∙ 2(-1) 0 3∙ 2(0) = 3∙ 1 3∙ 2(1) = 3∙ 2 6 2 3∙ 2(2) = 3∙ 4 12

GRAPHING: X y -2 -1 0 3 1 6 2 12 This graph grows fast = Exponential Growth

YOU TRY IT:

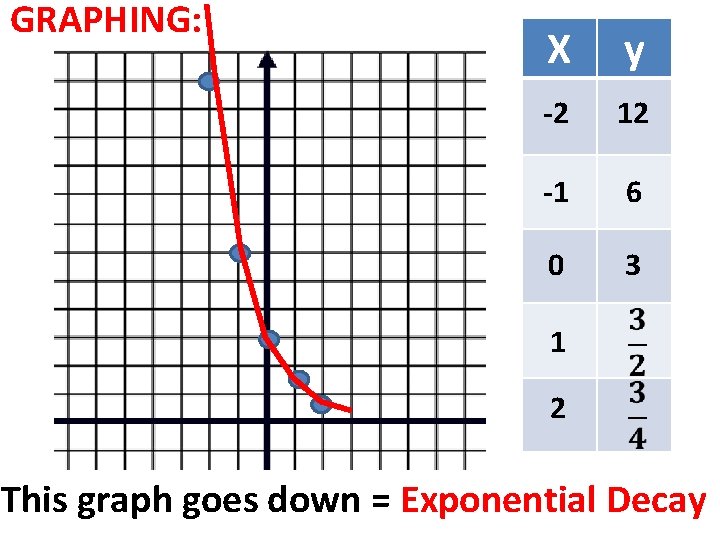
GRAPHING: X y -2 =3∙(2)2 12 -1 =3∙(2)1 6 0 = 3∙ 1 3 1 2

GRAPHING: X y -2 12 -1 6 0 3 1 2 This graph goes down = Exponential Decay

VIDEOS: Exponential Functions Growth https: //www. khanacademy. org/math/trigonometry/expo nential_and_logarithmic_func/exp_growth_decay/v/expo nential-growth-functions Graphing https: //www. khanacademy. org/math/trigonometry/expo nential_and_logarithmic_func/exp_growth_decay/v/graph ing-exponential-functions

VIDEOS: Exponential Functions Decay https: //www. khanacademy. org/math/trigonometry/expo nential_and_logarithmic_func/exp_growth_decay/v/wordproblem-solving--exponential-growth-and-decay

CLASSWORK: Page 450 -451: Problems: As many as needed to master the concept.