27 Determinants and Inverses Every square matrix has







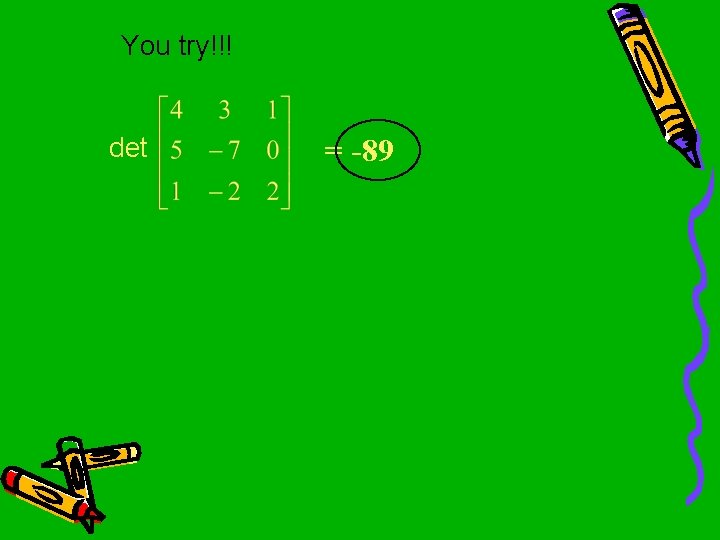




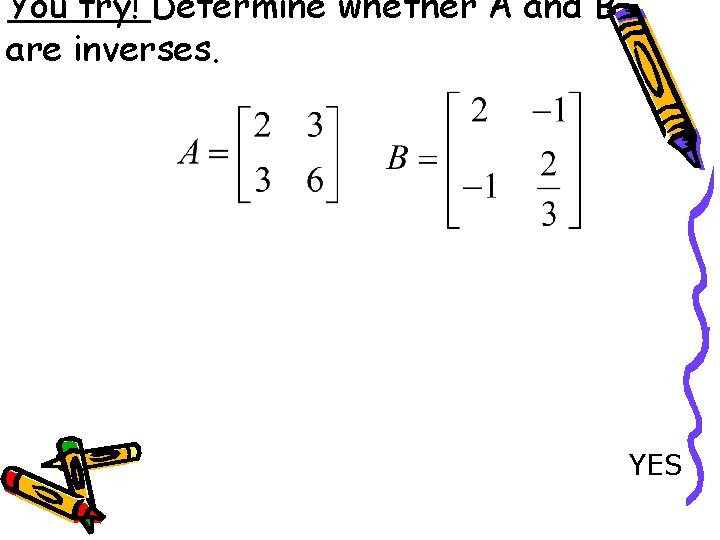

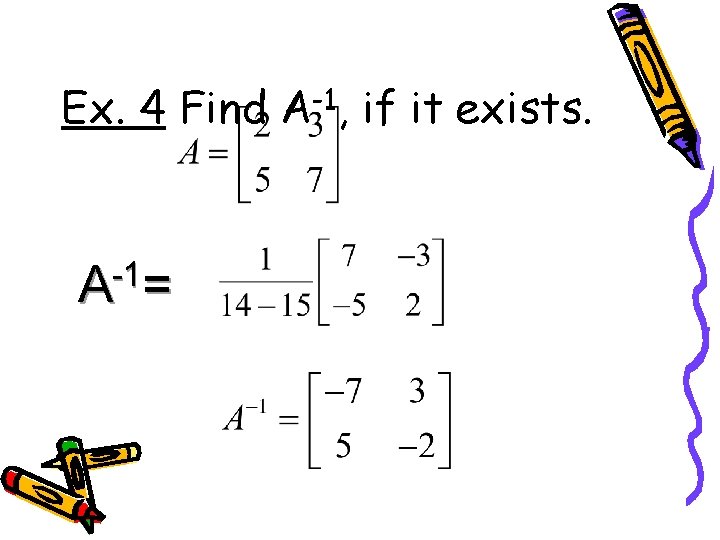
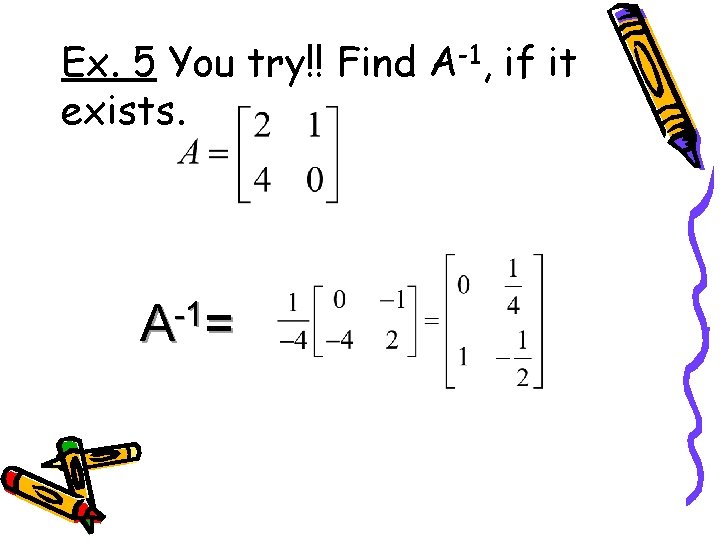
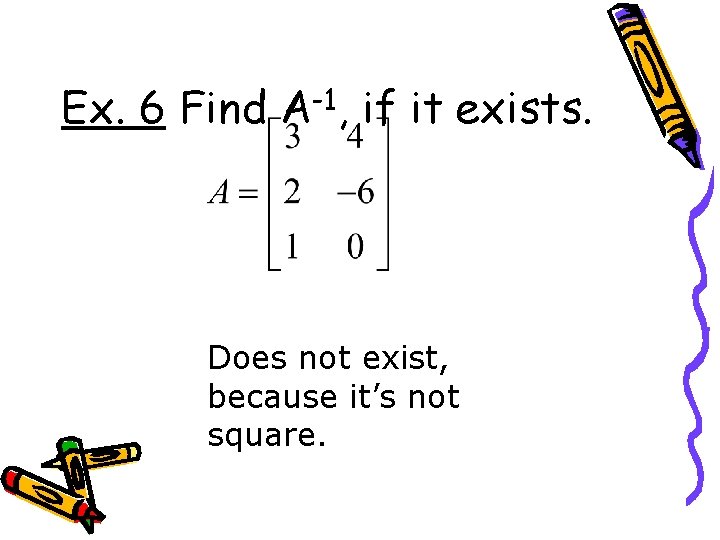

- Slides: 22

27. Determinants and Inverses

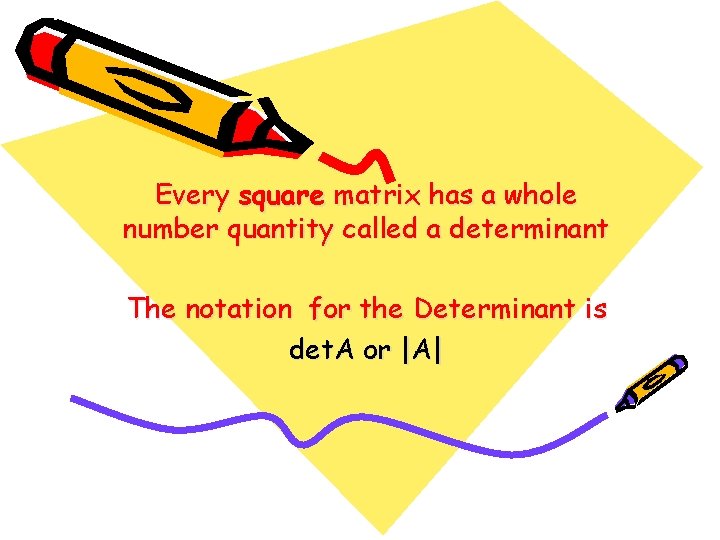
Every square matrix has a whole number quantity called a determinant The notation for the Determinant is det. A or |A|

Why they are important • • Used to find inverse of matrix Used to find area of region Used in decoding/encoding messages Used to help find equation of line

Determinant of a 2 x 2 = ad - cb

Evaluate the determinant =1(7) - 4(2) =7 -8 = -1

Evaluate the determinant =7(3) — 2(2) = 21 - 4 = 17

Steps for finding determinant of a 3 x 3 matrix Step 1: recopy the first two columns. Step 2: multiply down the diagonals and add the products Step 3: multiply up diagonals and add the products Step 4: Subtract the up diagonal from the down diagonal (down – up)

Evaluate 2 -3 Step 1: recopy the first two columns. Step 2: multiply the down diagonals and add the products. -2 0 1 2 = (2*0*6 + -3*3*1 + 4*-2*2) _ (1*0*4 + 2*3*2 + 6*-2*-3) = (0 + -9 + -16) – (0 + 12 + 36) = -25 - 48 Step 3: multiply the = -73 up diagonals and add the products NOTE: You subtract the up diagonal from the down diagona
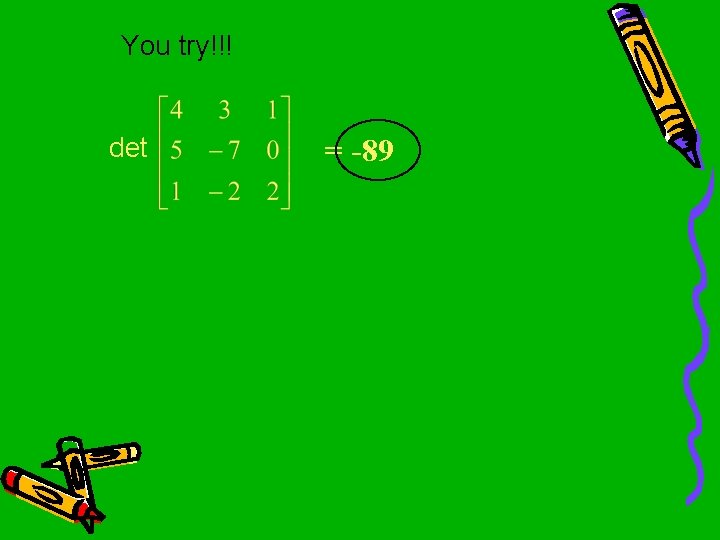
You try!!! det = -89

Determinants on calculator

Identity What is the multiplicative identity for the real numbers? In other words, 5 * __= 5? The identity for multiplication is 1 because anything multiplied by 1 will be itself.

What do we multiply by to get the identity? In other words, 5 * ___=1? a * -1 a = 1 Any number multiplied by its inverse will be the identity.

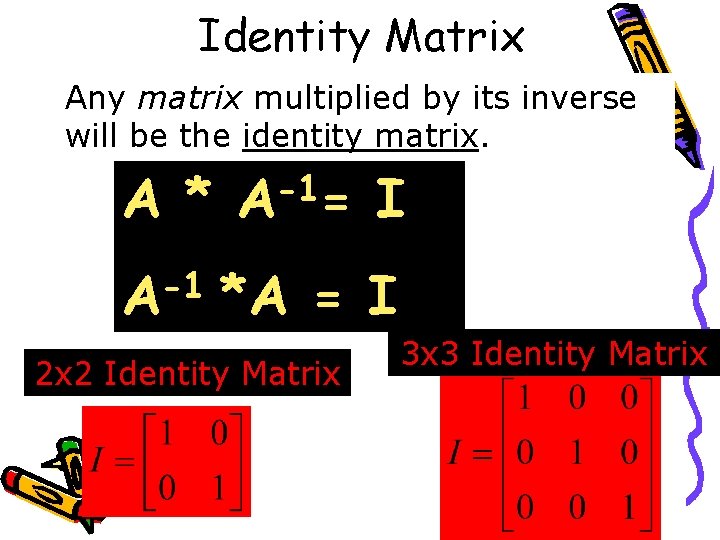
Identity Matrix Any matrix multiplied by its inverse will be the identity matrix. A * -1 A = I *A = I 2 x 2 Identity Matrix 3 x 3 Identity Matrix

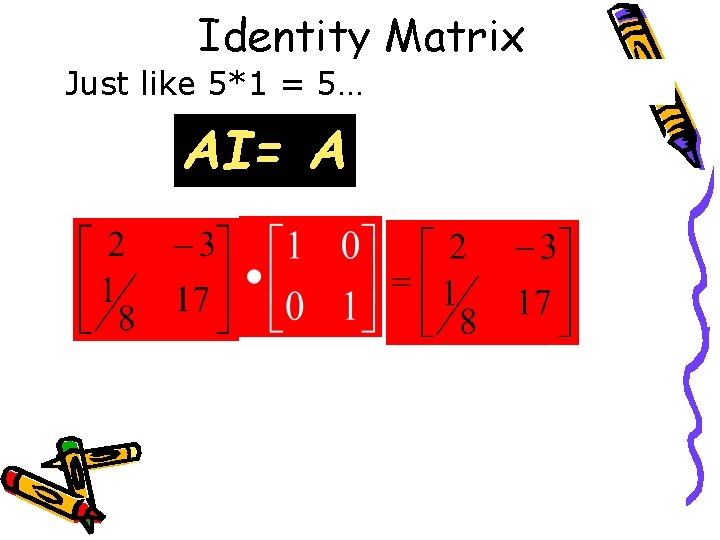
Identity Matrix Just like 5*1 = 5… AI= A

To find out if matrices are inverses: Find out if AB = I If so, then yes they’re inverses. If not, then no they’re not inverses. Ex. 1 Determine whether A and B are inverses. YES
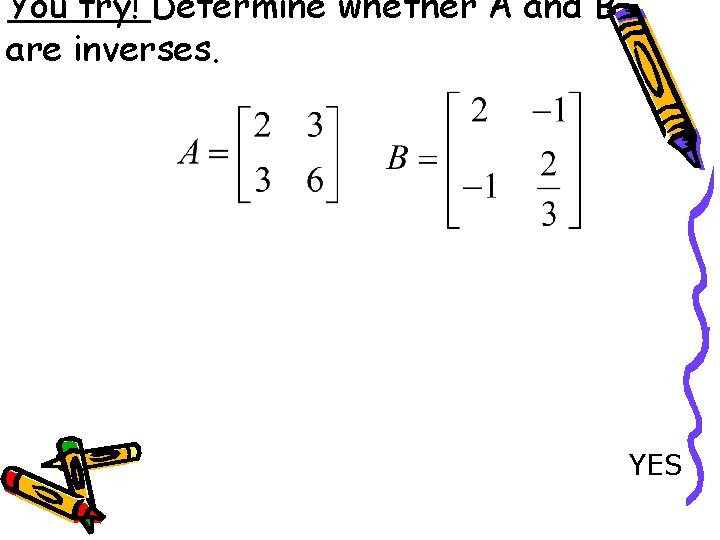
You try! Determine whether A and B are inverses. YES

The Inverse of a 2 x 2 Matrix -1 A = As long as the determinant does not equal 0 If the determinant=0, then the matrix has no inverse!!!!
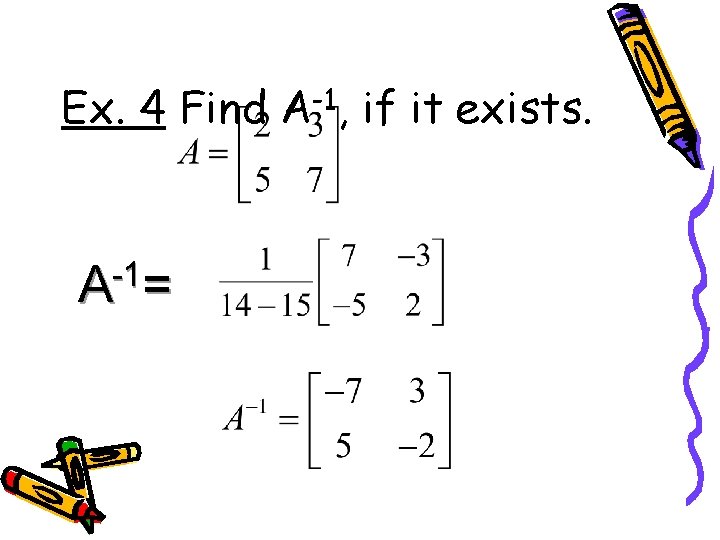
Ex. 4 Find A-1, if it exists. -1 A =
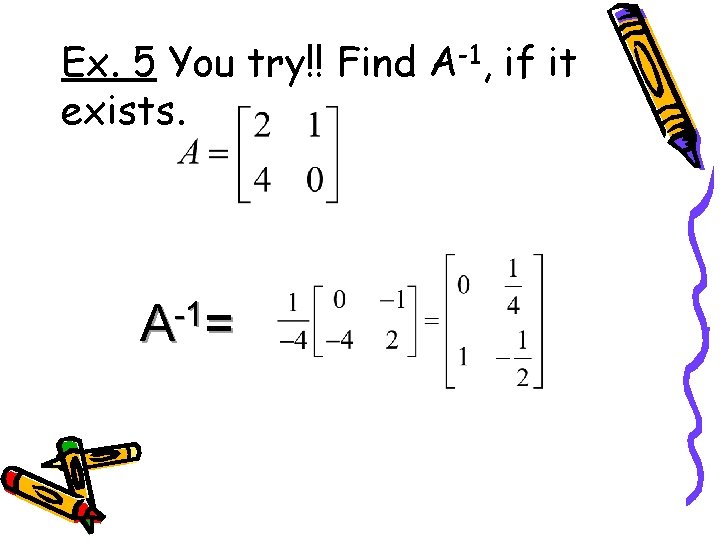
Ex. 5 You try!! Find A-1, if it exists. -1 A =
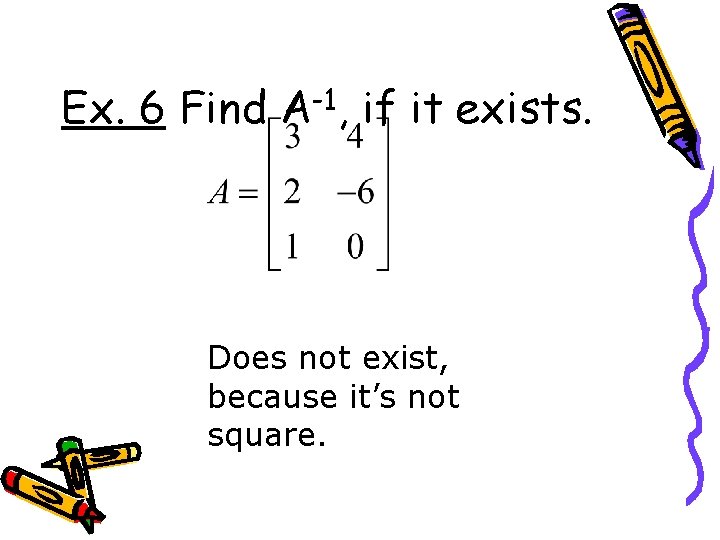
Ex. 6 Find A-1, if it exists. Does not exist, because it’s not square.

Inverses on calculator

Ticket out the Door Answer the essential question: What is a determinant and why does it matter?