2 Koordintarendszerek s transzformcik 2 1 Koordintarendszerek 2




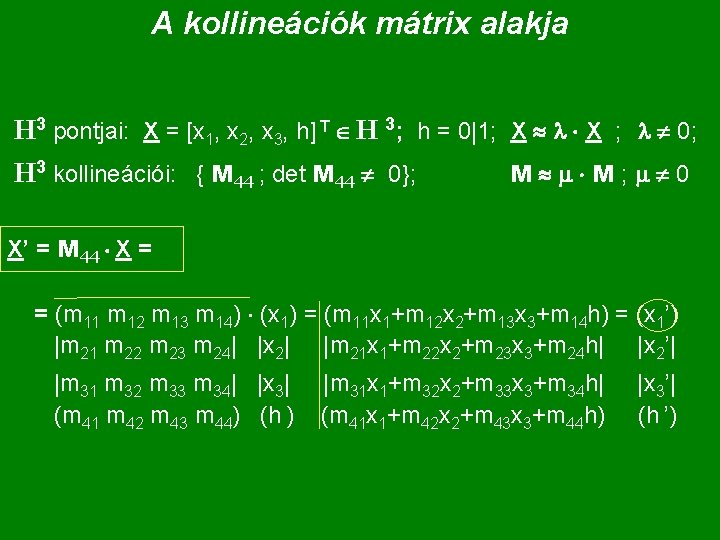
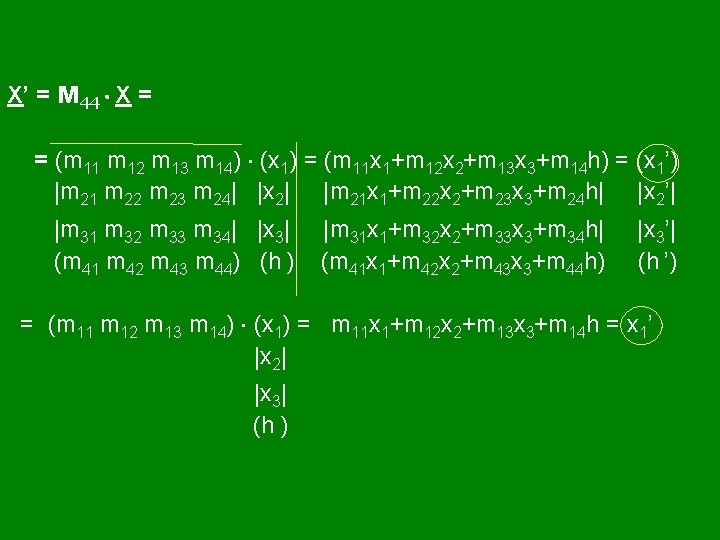



















- Slides: 32

2. Koordináta-rendszerek és transzformációk 2. 1. Koordináta-rendszerek 2. 2. Az egyenes és a sík egyenlete 2. 3. Affin transzformációk 2. 4. Projektív transzformációk

Mire használjuk? • Transzformációk a grafikában: - tárgyak elhelyezése, - részek összeállítása - tárgyak valószerű átalakításai (GM), - a tárgyak képe: vetítés síkra - egyebek

Milyen transzformációk kellenek? - E 3 –ban és H 3 -ban ( H 3 = E 3 I 3 ) - minden pontnak van transzformáltja, - H 3 (kölcsönösen egyértelmű) - pontot pont, - egyenes - sík - illeszkedést tartó módon. Ilyenek a kollineációk, (projektív transzformációk)

Kollineációk (projektív transzformációk) • Kollineációk a projektív geometriában. . . • Itt: a transzformációk geometriai, szemléletes jelentése. . . • A transzformációk számítási eljárásai: Pontok transzformációja: X’ = M 44 X Egyenes transzformációja: Ha e = ( P, Q ), akkor e’ = ( P’, Q’ ) ; P’ = M 44 P , Q’ = M 44 Q stb: alakzatok meghatározó pontjait. . .
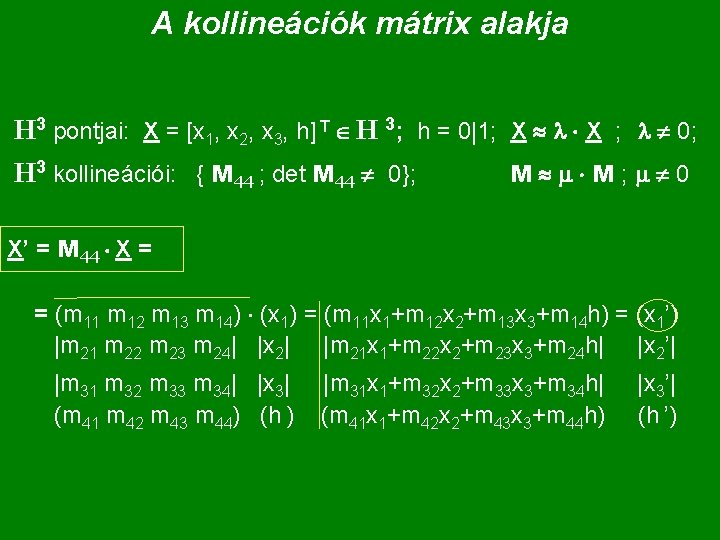
A kollineációk mátrix alakja H 3 pontjai: X = [x 1, x 2, x 3, h] T H 3; h = 0|1; X l X ; l 0; H 3 kollineációi: { M 44 ; det M 44 0}; M m M; m 0 X’ = M 44 X = = (m 11 m 12 m 13 m 14) (x 1) = (m 11 x 1+m 12 x 2+m 13 x 3+m 14 h) = (x 1’) |m 21 m 22 m 23 m 24| |x 2| |m 21 x 1+m 22 x 2+m 23 x 3+m 24 h| |x 2’| |m 31 m 32 m 33 m 34| |x 3| (m 41 m 42 m 43 m 44) (h ) |m 31 x 1+m 32 x 2+m 33 x 3+m 34 h| (m 41 x 1+m 42 x 2+m 43 x 3+m 44 h) |x 3’| (h ’)
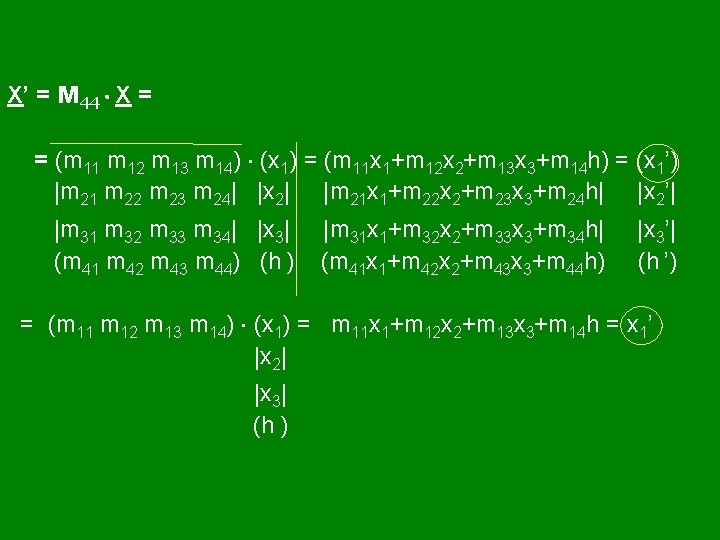
X’ = M 44 X = = (m 11 m 12 m 13 m 14) (x 1) = (m 11 x 1+m 12 x 2+m 13 x 3+m 14 h) = (x 1’) |m 21 m 22 m 23 m 24| |x 2| |m 21 x 1+m 22 x 2+m 23 x 3+m 24 h| |x 2’| |m 31 m 32 m 33 m 34| |x 3| (m 41 m 42 m 43 m 44) (h ) |m 31 x 1+m 32 x 2+m 33 x 3+m 34 h| (m 41 x 1+m 42 x 2+m 43 x 3+m 44 h) |x 3’| (h ’) = (m 11 m 12 m 13 m 14) (x 1) = m 11 x 1+m 12 x 2+m 13 x 3+m 14 h = x 1’ |x 2| |x 3| (h )

E 3 és H 3 kollineációi: csoport • E 3 kollineációi: affin transzformációk, alcsoport, E 3 és I 3 • H 3 kollineációi: a projektív transzformációk csoportja H 3, egy – egyértelmű leképezés, pont-, egyenes-, sík- és illeszkedést tartó H 3=E 3 I 3 esetleg egy közönséges sík I 3 és akkor I 3 egy közönséges síkra

A következő órákon: Affin transzformációk Párhuzamos vetítés Axonometria Projektív transzformáció Középpontos vetítés Perspektíva

2. 3. 1. Affin transzformációk (a grafikában – szemléletes bevezetés)

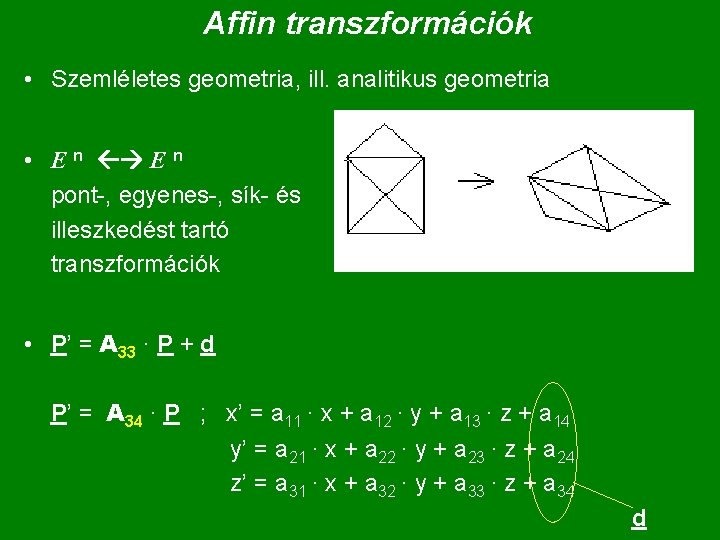
Affin transzformációk • Szemléletes geometria, ill. analitikus geometria • E n pont-, egyenes-, sík- és illeszkedést tartó transzformációk • P’ = A 33 · P + d P’ = A 34 · P ; x’ = a 11 · x + a 12 · y + a 13 · z + a 14 y’ = a 21 · x + a 22 · y + a 23 · z + a 24 z’ = a 31 · x + a 32 · y + a 33 · z + a 34 d

Affin transzformációk § Például: eltolás, forgatás, tükrözés, stb § Reguláris affinitások: det A 0; E n ; n = 2, 3, … (Ha det A = 0 : vetítés egy síkra, vagy más altérre) § Szóhasználat: affin transzformáció, affinitás (? ), transzformáció, leképezés § Pont-transzformáció: alakzatok pontjait Koordináta-rendszer transzformáció: áttérés új KR-re A tér leképezése egy másik térre pl. VKR KKR

Affin transzformáció mátrix-szorzással • Homogén mátrix alakja: A 44 utolsó sora: (0, 0, 0, c) ; c 0; általában = 1 • Egy pont homogén alakja: X = [x, y, z, h] T ; h = 0 | 1 • • X’ = A 44 X = (a 11 a 12 a 13 a 14 ) (x) = (x’) ; |a 21 a 22 a 23 a 24 | |y’| |a 31 a 32 a 33 a 34 | |z’| ( 0 0 0 1 ) (h’); h=0|1 h’ = h !!! közönséges pont, ideális pont: az ideális sík önmaga.

Affin transzformációk • A mátrix megadása: – geometria jelentése alapján: szemléletes elemi affinitások szorzataként – vagy 4 meghatározó pont-párból: a „határozatlan együtthatók módszere”

„Elemi” affin transzformációk • „elemi”: szemléletes és egyszerű a mátrixa • Eltolás (T) , forgatás (R), léptékezés (S) , nyírás (N) • Tükrözés, báziscsere, • Tétel: Ha A affin traanszformáció, akkor van olyan T, R 1, R 2, R 3, S, N, a • amelyekkel: A = N S O T; O = R 1 R 2 R 3 • azaz: P ’ = A P = (N S O T) P • Minden A ilyenekből áll !

A mátrix vizsgálata § A mátrix jellemző elemei: A 44 = (sx a 12 a 13 dx ); |a 21 sy a 23 dy | |a 31 a 32 sz dz | (0 0 0 1) det A 0 ; > 1 | < 1

Egyszerű affinitások: 1. Eltolás • Adott: d = (dx, dy, dz) eltolás-vektor • Minden pontra: X’ = X + d = (x + dx, y + dy, z + dz) d • X’ = T X = (X + d) (x’) = ( 1 0 0 dx ) · (x) = ( x + dx ) |y’| | 0 1 0 dy | |y| | y + dy | |z’| | 0 0 1 dz | |z| | z + dz | (1 ) ( 0 0 0 1 ) (1) ( 1 ) • T 2 (T 1 P) = (T 2 T 1) P = T 3 P

Egysz. aff. 2. Forgatás a Z tengely körül • x’ = x cos a - y sin a y’ = x sin a + y cos a z’ = z; Rz = (co –si | si co | 0 0 ( 0 0 • A síkban: a kezdőpont (origó) körül: a 3. sor és 3. oszlop nélkül • a Z tengely körüli forgatások kommutatív csoportja: • Ortonormált transzformáció, determinánsa 1. 0 0 1 0 co = cos a si = sin a 0) 0| 0| 1)

Forgatás az X és az Y tengely körül • x’ = x y’ = y cos a - z sin a z’ = y sin a + z cos a • illetve: x’ = x cos a – z sin a y’ = y z’ = x sin a + z cos a • egyazon tengely körüli forgatások kommutatív csoportot alkotnak Rx = (1 |0 |0 (0 0 0 co –si si co 0 0 Ry = (co |0 |si (0 0) 0| 0| 1) 0 –si 0) 1 0 0| 0 co 0| 0 0 1) co = cos a si = sin a

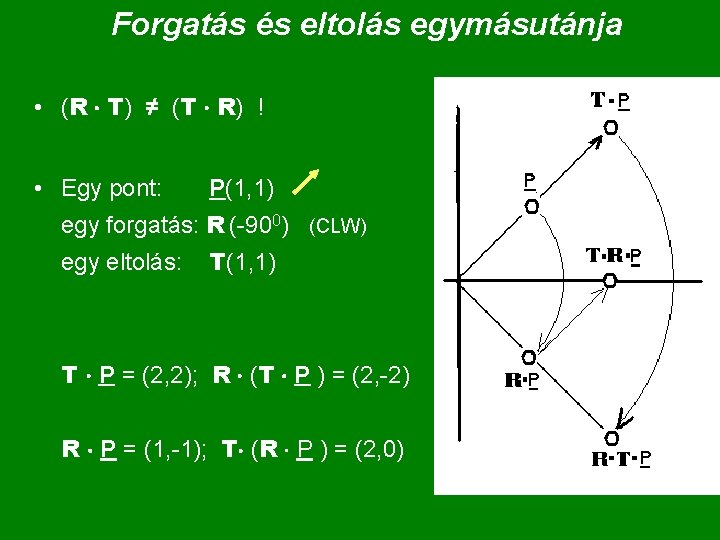
Forgatás és eltolás egymásutánja • (R T) ≠ (T R) ! • Egy pont: P(1, 1) egy forgatás: R (-900) (CLW) egy eltolás: T(1, 1) T P = (2, 2); R (T P ) = (2, -2) R P = (1, -1); T (R P ) = (2, 0)

Forgatások a térben • az origón átmenő (ferde) tengely körül: X’ = R* X = [ (R • -1 z R x -1) R y (a) (R x R z) ] X Z A ferde tengely (a terem sarkán át) 1. a Z körül a ZY síkba : R z 2. itt az X körül az Y-tengelybe : R 3. Az Y körül a kívánt forgatást: R y (a) x 4 -5. Végül az 1. -2. fordítottját (fordított sorrendben). X Y

Forgatások a térben - 2 • Forgatás tetszőleges tengely körül. • A tengely (egy pontját) eltoljuk O-ba: T • és ekörül forgunk (mint előbb): R*(a) • Végül az eltolás fordítottja: X’ = (T-1 R*(a) T) X • Transzformációk megadása: szemléletes elemi geometria transzformációk sorozatával !!

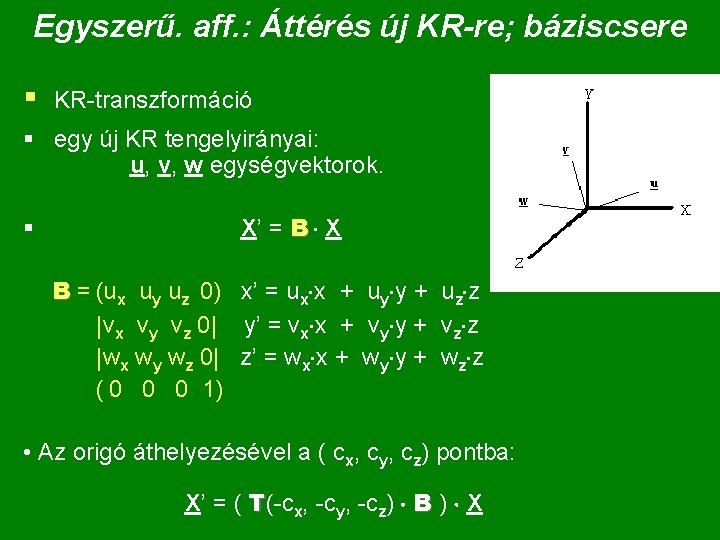
Egyszerű. aff. : Áttérés új KR-re; báziscsere § KR-transzformáció § egy új KR tengelyirányai: u, v, w egységvektorok. § X’ = B X B = (ux uy uz 0) x’ = ux x + uy y + uz z |vx vy vz 0| y’ = vx x + vy y + vz z |wx wy wz 0| z’ = wx x + wy y + wz z ( 0 0 0 1) • Az origó áthelyezésével a ( cx, cy, cz) pontba: X’ = ( T(-cx, -cy, -cz) B ) X

Egysz. aff. : 3. Léptékezés (skálázás) • Léptékezés (skálázás) az origóból kiindulva: X’ = S X S = ( sx 0 0 0 ) x’ = sx x | 0 sy 0 0 | y’ = sy y | 0 0 sz 0 | z’ = sz z (0 0 0 1) • Determinánsa: D = sx sy sz ; (egyik sem nulla). • Egyenletes (izotrop) léptékezés: sx= sy= sz Egyenlőtlen (anizotrop) különben

Tükrözések: si < 0 • x’ = -1 · x, y’ = y, z’ = z : tükrözés az YZ síkra. • Tükrözések: S( 1, 1, 1) • Ha 1 tényező negatív: tükrözés koordináta-síkra, (det = -1) ha 2 koordináta tengelyre, (det = +1) ha 3 a kezdőpontra. (det = -1) • Ha det = -1, a tér irányítása megfordul ! • Általános helyzetű tükrözés: X’ = (ÁTHELYEZÉS -1 TÜKRÖZÉS ÁTHELYEZÉS ) X • Mozgatás: eltolások és forgatások; méret és alaktartó

Tengelycsere • (A teljesség kedvéért : ) • Permutációs mátrixok; például: Cyz = ( 1 0 0 0 ) · [ x ] = [ x ] |0010| |y| |z| |0100| |z| |y| ( 0 0 0 1 ) [1 ] [ 1] az Y és Z tengelyt fölcseréli determinánsa = -1 !!!

Egysz. aff. : 4. Nyírás § Merev test alakjának változása terhelés hatására. § Az „elcsúszó kártyacsomag” § Az XZ síkkal párhuzamosan, X irányban, az y összetevővel arányos nyírás: x’ = x + a y ; X’ = Nxy X; Nxy = ( 1 a 0 0 ) y’ = y | 01 0 0 | z’ = z |0010| (0 0 0 1 ) § Nyírás a tengelyek más szereposztásával: más háromszög mátrix

Az affin transzformációk néhány tulajdonsága 1. A baricentrikus koordináták affin-invariánsak: ha valamilyen t-vel: akkor ugyanezzel : 2. Az egyenes pontjainak osztóviszonya affin-invariáns: (P’Q’R’) = (PQR); 3. R = (1 - t) P + t Q, R’= (1 - t) P’ + t Q’ (P’, Q’, R’) = A (P, Q, R) (PQR) = PR / RQ; R Q Párhuzamos szakaszok hossza egyforma arányban változik: P’Q’ / PQ = R’S’ / RS, ha PQ || RS (Különböző irányokban az arány különböző lehet)

Az affin transzformációk osztályozása § csoportot alkotnak § Alcsoport: hasonlósági transzformációk : T R S(s, s, s) § Alcsoport: mozgás transzformációk : T R = egybevágósági transzformációk „Másodfajú” egybevágóság: a tükrözés is. § Ha det A = 0: a tér vetítése egy síkra, vagy egyenesre

Elhelyező transzformáció: hasonlóság SKR VKR; M=T S R

Affin transzformáció megadása: 4 -4 pont § E 3 egy affinitását meghatározza 4 „független” pont és képe. (E 2 -ben 3) § „független”: kifeszítik a teret egyik három sem esik egyenesbe.

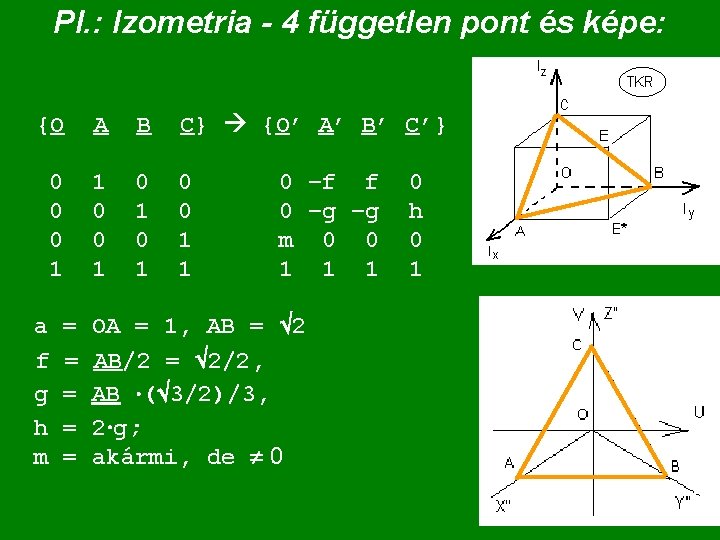
Pl. : Izometria - 4 független pont és képe: {O A B C} {O’ A’ B’ C’} 0 0 0 1 1 0 0 1 0 1 0 0 1 1 a f g h m = = = 0 –f f 0 –g –g m 0 0 1 1 1 OA = 1, AB = 2 AB/2 = 2/2, AB ( 3/2)/3, 2 g; akármi, de 0 0 h 0 1

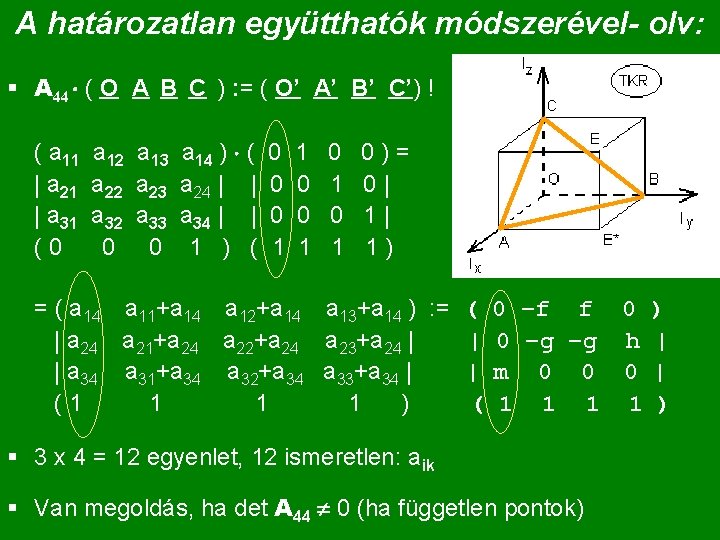
A határozatlan együtthatók módszerével- olv: § A 44 ( O A B C ) : = ( O’ A’ B’ C’) ! ( a 11 | a 21 | a 31 (0 a 12 a 13 a 22 a 23 a 32 a 33 0 0 a 14 ) ( a 24 | | a 34 | | 1 ) ( 0 0 0 1 1 0 0 1 0 1 0)= 0| 1| 1) = ( a 14 a 11+a 14 a 12+a 14 a 13+a 14 ) : = ( 0 –f f 0 ) | a 24 a 21+a 24 a 22+a 24 a 23+a 24 | | 0 –g –g h | | a 34 a 31+a 34 a 32+a 34 a 33+a 34 | | m 0 0 0 | (1 1 ) ( 1 1 ) § 3 x 4 = 12 egyenlet, 12 ismeretlen: aik § Van megoldás, ha det A 44 0 (ha független pontok)
















