A geometriai transzformcik 9 vfolyam Trtneti elzmnyek A

A geometriai transzformációk 9. évfolyam

Történeti előzmények • A geometria a matematika térbeli törvényszerűségek, összefüggések leírásából kialakult ága; maga a geometria szó görögül eredetileg földmérést jelentett. • Az elemi geometriában az egybevágóság, hasonlóság és általában a transzformáció fogalmai alapvetőek.

Geometria tanítása a középkori Franciaországban (1300 -as évek eleje)

A geometriai transzformáció fogalma • A geometriai transzformációk olyan speciális függvények, amelyeknek értelmezési tartománya és értékkészlete is ponthalmaz.

Milyen tulajdonságokat vizsgálunk? 1. Kölcsönösen is egyértelmű-e a hozzárendelés? A geometriai transzformáció kölcsönösen egyértelmű, ha egy pontnak egy képpont felel meg, és minden képpontnak egy őse van. Például ilyen a tengelyes tükrözés.

2. Szimmetrikus e a hozzárendelés? A geometriai transzformáció akkor szimmetrikus, ha P képe P* esetén, P* képe P. Ilyen például a középpontos tükrözés:

3. Vannak e fixpontok? Egy geometriai transzformációnál fixpont az a pont, amelynek képe önmaga. Például a középpontos tükrözésnél a tükrözés középpontja. 4. Vannak e invariáns alakzatok? Ha az alakzat képe önmaga, akkor invariáns alakzatnak nevezzük. (A pontjai nem kell, hogy fixpontok legyenek!) Például: e=e' t

5. Egyenestartó e? Egyenestartónak nevezzük a geometriai transzformációt, ha egyenes képe is egyenes. 6. Távolságtartó e? A geometriai transzformációk közül a távolság- tartó leképezések azok, amelyeknél: ha a P és Q pont képe P' és Q', akkor P és Q távolsága megegyezik a P' és Q' távolságával. 7. Szögtartó e? A geometriai transzformáció szögtartó, ha szög és képe egyenlő nagyságú.

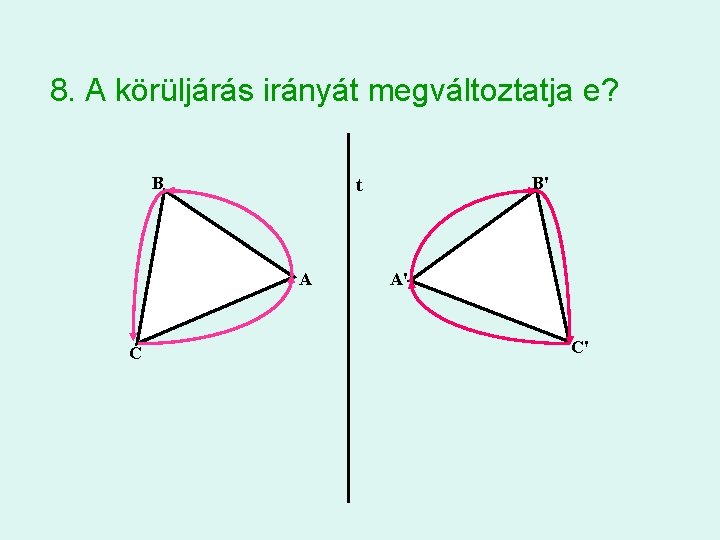
8. A körüljárás irányát megváltoztatja e? B A C B' t A' C'

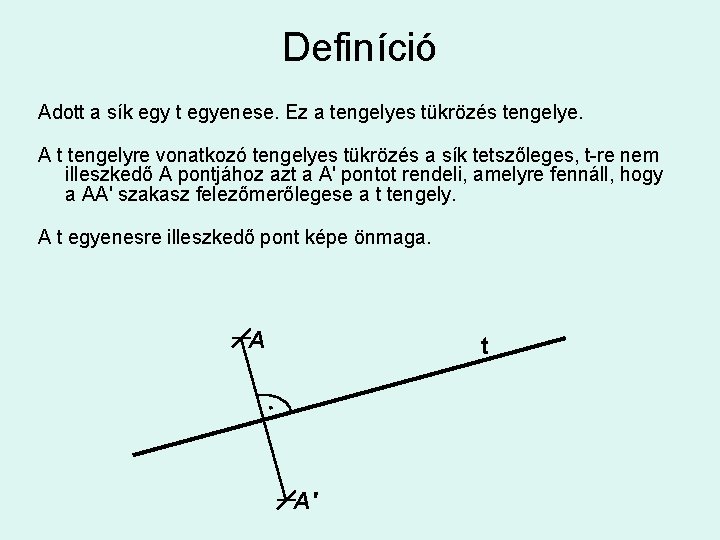
Definíció Adott a sík egy t egyenese. Ez a tengelyes tükrözés tengelye. A t tengelyre vonatkozó tengelyes tükrözés a sík tetszőleges, t-re nem illeszkedő A pontjához azt a A' pontot rendeli, amelyre fennáll, hogy a AA' szakasz felezőmerőlegese a t tengely. A t egyenesre illeszkedő pont képe önmaga. A t A'

A tengelyes tükrözés tulajdonságai: 1. kölcsönösen egyértelmű, 2. szimmetrikus, 3. a t egyenes minden pontja fixpont, 4. invariáns alakzatok például a t egyenesre merőleges egyenesek,

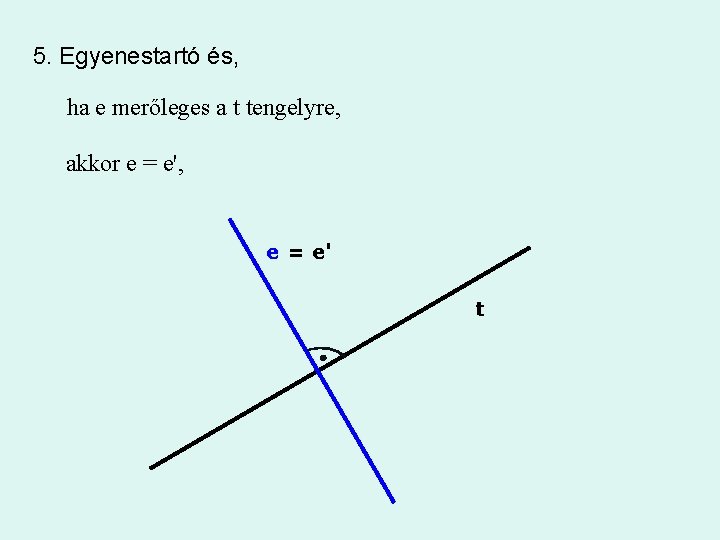
5. Egyenestartó és, ha e merőleges a t tengelyre, akkor e = e', e = e' t

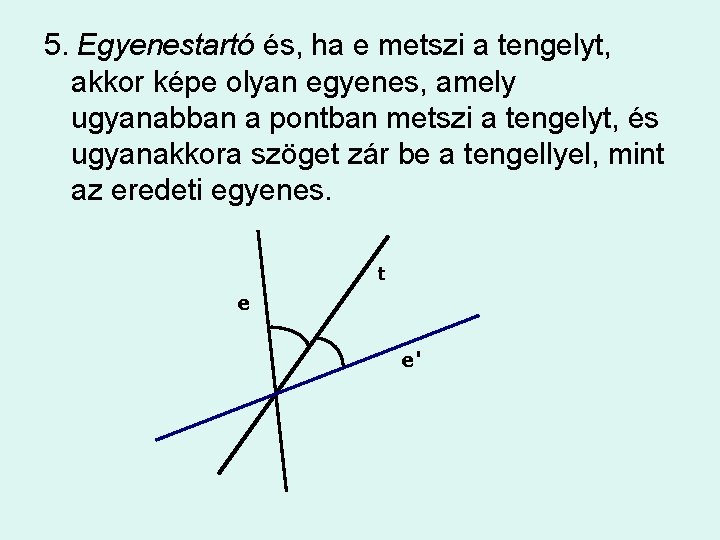
5. Egyenestartó és, ha e metszi a tengelyt, akkor képe olyan egyenes, amely ugyanabban a pontban metszi a tengelyt, és ugyanakkora szöget zár be a tengellyel, mint az eredeti egyenes. t e e'

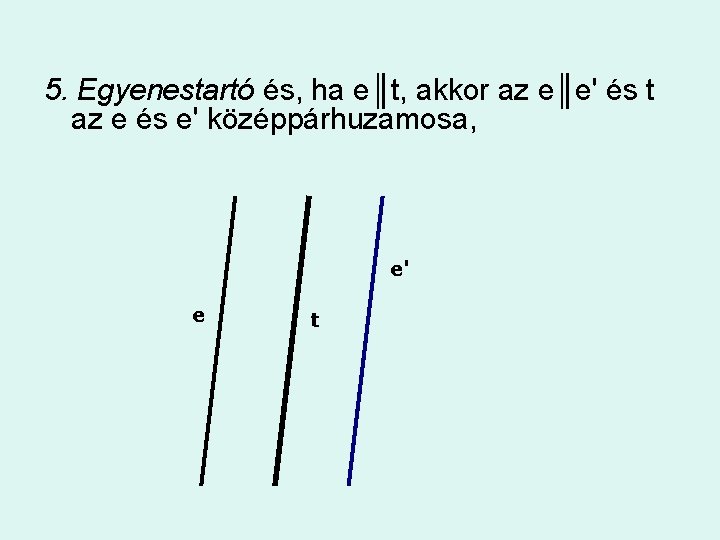
5. Egyenestartó és, ha e║t, akkor az e║e' és t az e és e' középpárhuzamosa, e' e t

A tengelyes tükrözés további tulajdonságai: 6. távolságtartó, 7. szögtartó, 8. a körüljárás irányát megváltoztatja.

A tengelyes szimmetria Definíció: egy síkbeli alakzat tengelyesen szimmetrikus, ha az alakzat síkjában létezik olyan t egyenes, amelyre vonatkozó tükrözésnél az alakzat képe önmaga. A t egyenes az alakzat tükörtengelye, vagy szimmetriatengelye.

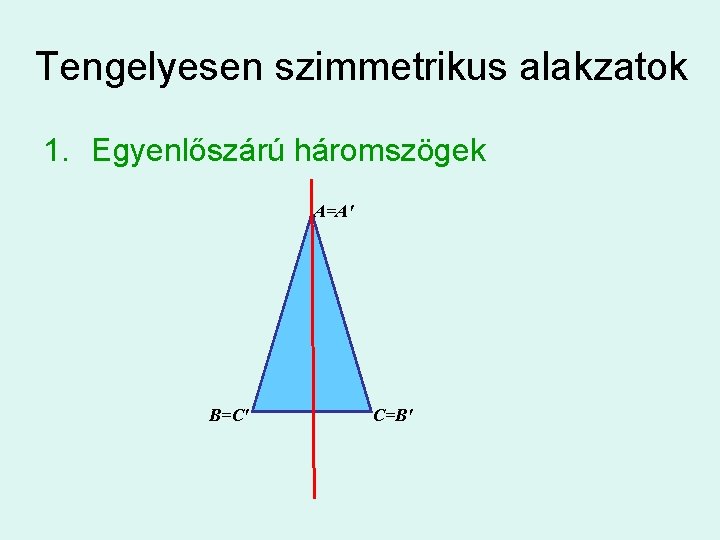
Tengelyesen szimmetrikus alakzatok 1. Egyenlőszárú háromszögek A=A' B=C' C=B'

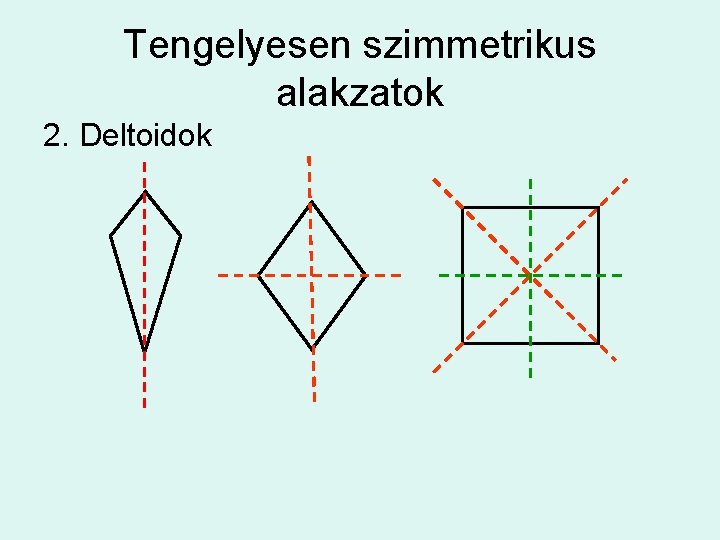
Tengelyesen szimmetrikus alakzatok 2. Deltoidok

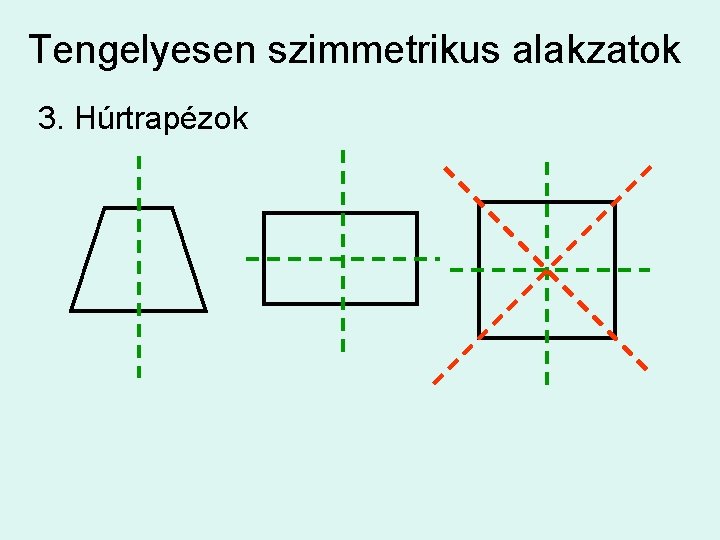
Tengelyesen szimmetrikus alakzatok 3. Húrtrapézok

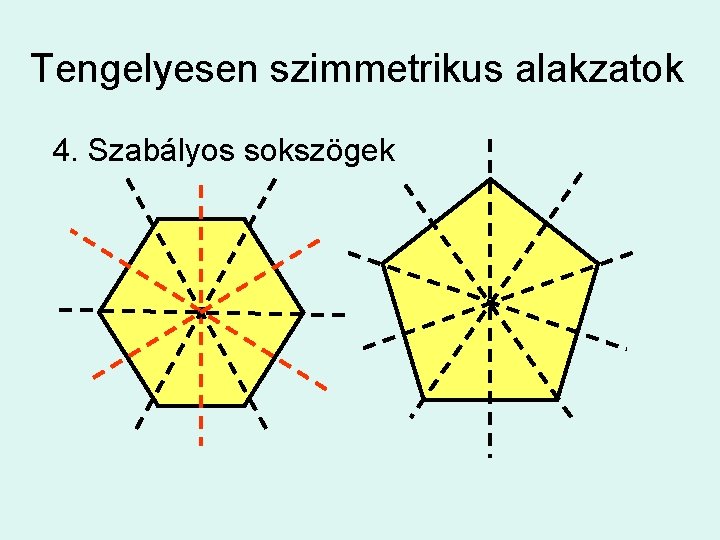
Tengelyesen szimmetrikus alakzatok 4. Szabályos sokszögek

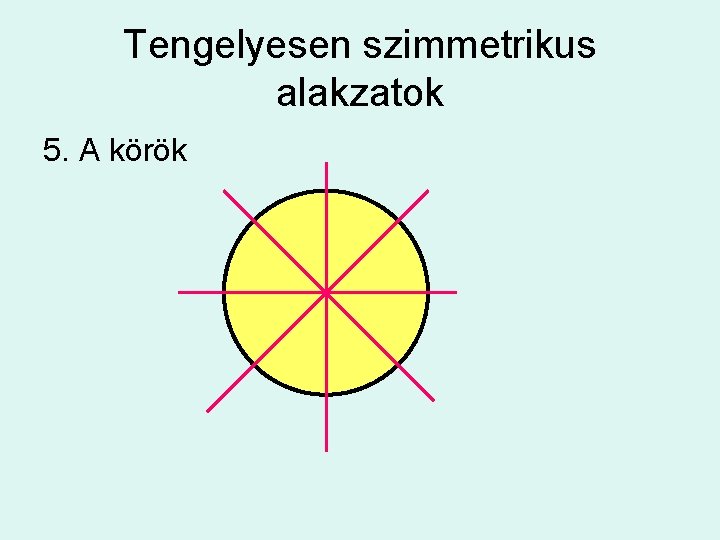
Tengelyesen szimmetrikus alakzatok 5. A körök

Példák a tengelyes szimmetriára a mindennapi életben

Példák a tengelyes szimmetriára a mindennapi életben

Példák a tengelyes szimmetriára a mindennapi életben

Példák a tengelyes szimmetriára: Victor Vasarely képei

A középpontos tükrözés definíciója Adott a sík egy O pontja, a középpontos tükrözés középpontja. Az O pontra vonatkozó középpontos tükrözés a sík tetszőleges O-tól különböző A pontjához azt az A' pontot rendeli, amelyre az O pont a AA' szakasz felezőpontja. Az O pont képe önmaga. O A A'

A középpontos tükrözés tulajdonságai: 1. kölcsönösen egyértelmű, 2. szimmetrikus, 3. fixpont a tükrözés középpontja, 4. invariáns alakzat például minden, a tükrözés középpontján áthaladó egyenes, és a tükrözés középpontjával azonos középpontú kör

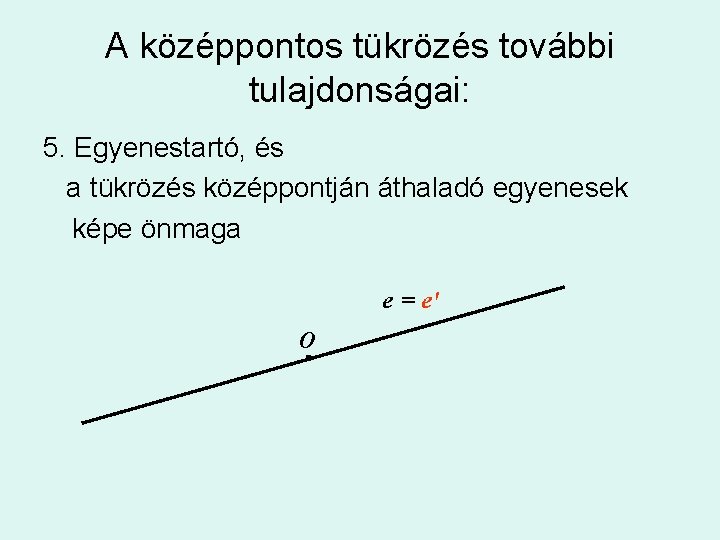
A középpontos tükrözés további tulajdonságai: 5. Egyenestartó, és a tükrözés középpontján áthaladó egyenesek képe önmaga e = e' O

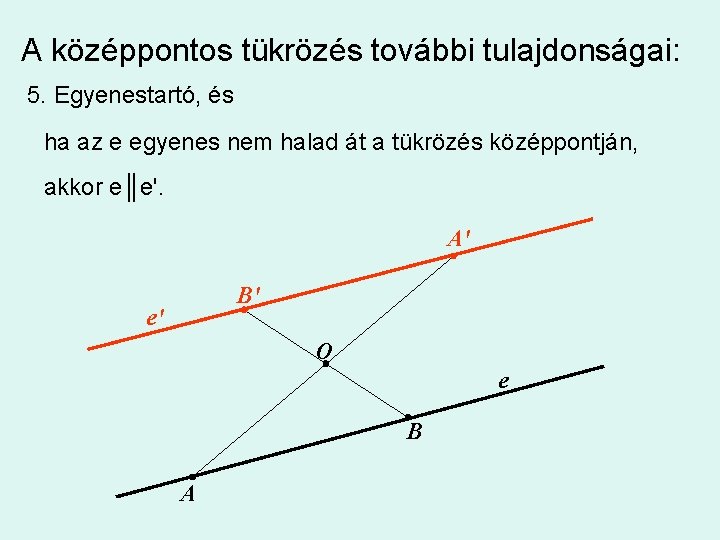
A középpontos tükrözés további tulajdonságai: 5. Egyenestartó, és ha az e egyenes nem halad át a tükrözés középpontján, akkor e║e'. A' B' e' O e B A

A középpontos tükrözés további tulajdonságai: 6. távolságtartó, 7. szögtartó, 8. a körüljárás irányát nem változtatja meg

A középpontos szimmetria Definíció: egy alakzat középpontosan szimmetrikus, ha létezik olyan pont, amelyre vonatkozó tükrözésnél az alakzat képe önmaga

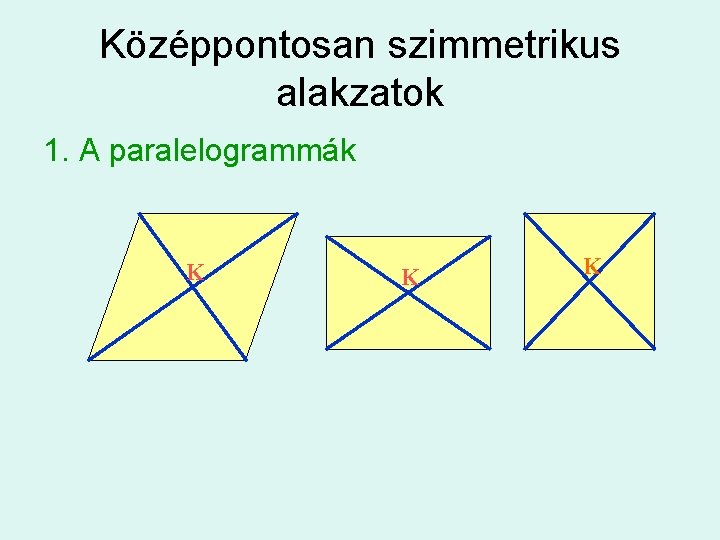
Középpontosan szimmetrikus alakzatok 1. A paralelogrammák K K K

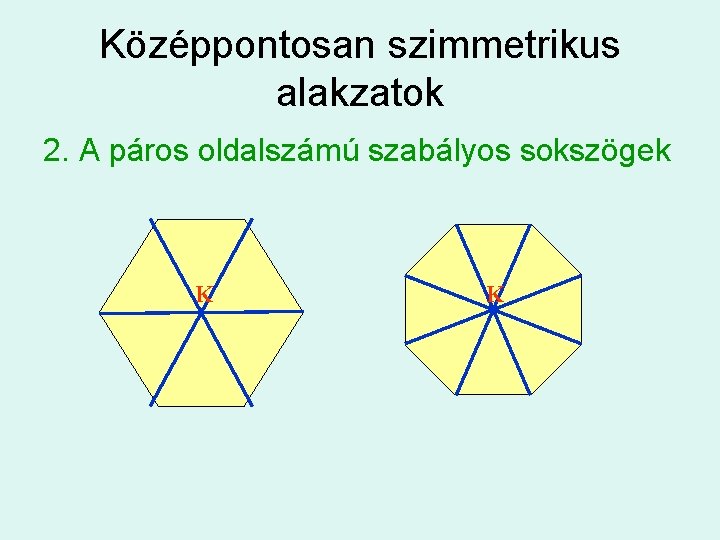
Középpontosan szimmetrikus alakzatok 2. A páros oldalszámú szabályos sokszögek K K

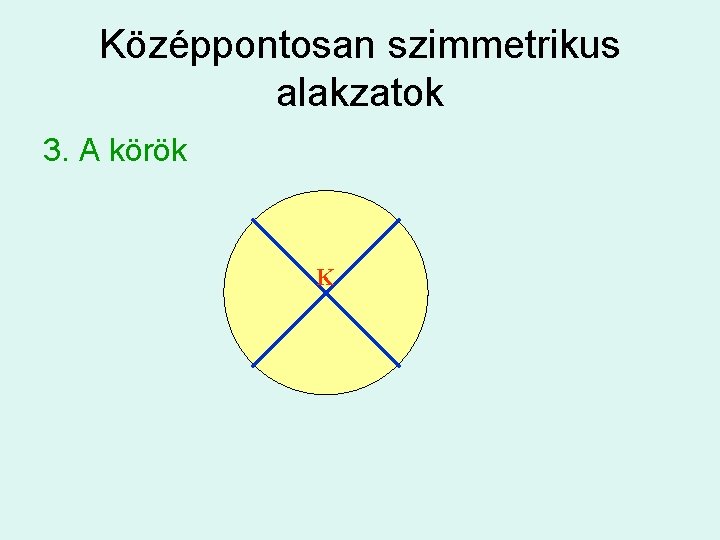
Középpontosan szimmetrikus alakzatok 3. A körök K

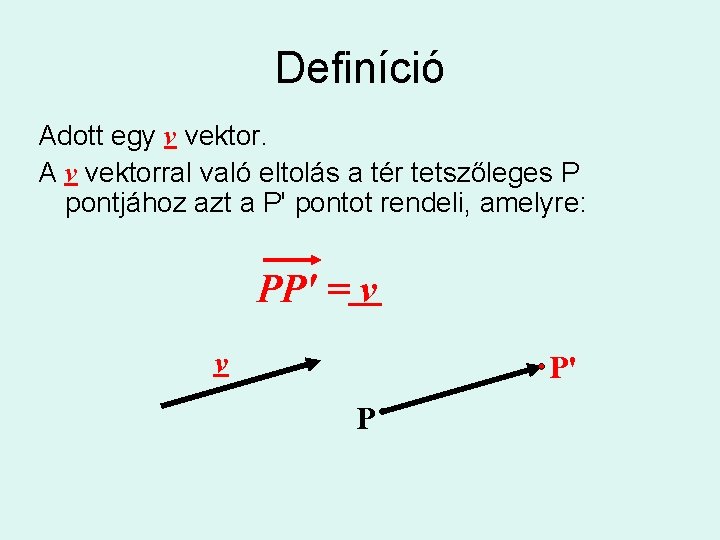
Definíció Adott egy v vektor. A v vektorral való eltolás a tér tetszőleges P pontjához azt a P' pontot rendeli, amelyre: PP' = v v P' P

Az eltolás tulajdonságai: 1. kölcsönösen egyértelmű, 2. nem szimmetrikus 3. nincs fixpontja, kivéve ha az adott vektor nullvektor, 4. az adott vektorral párhuzamos egyenesek és síkok invariáns alakzatok, 5. távolságtartó, 6. szögtartó, 7. a körüljárás irányát nem változtatja meg

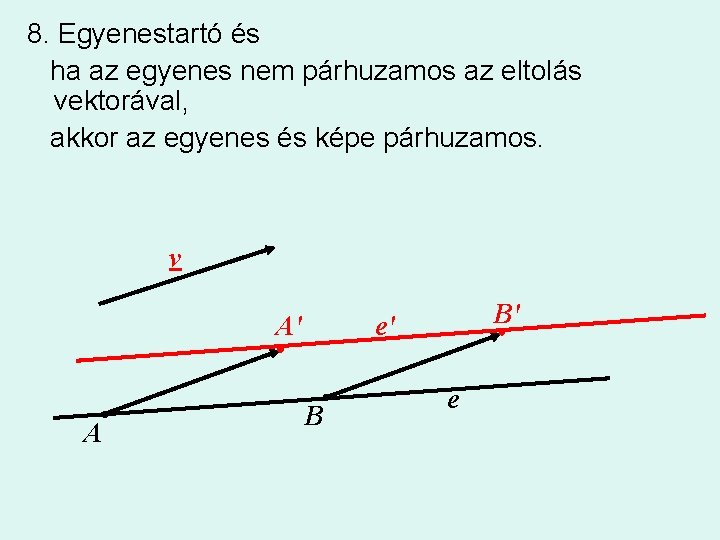
8. Egyenestartó és ha az egyenes nem párhuzamos az eltolás vektorával, akkor az egyenes és képe párhuzamos. v A' A B' e' B e

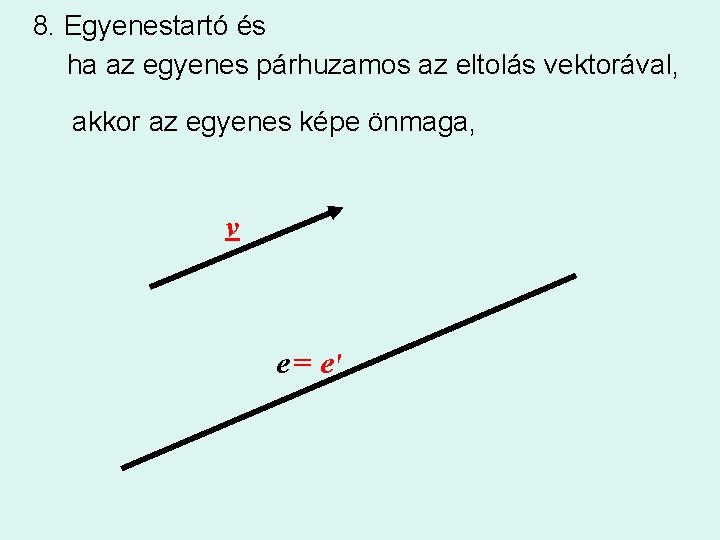
8. Egyenestartó és ha az egyenes párhuzamos az eltolás vektorával, akkor az egyenes képe önmaga, v e = e'

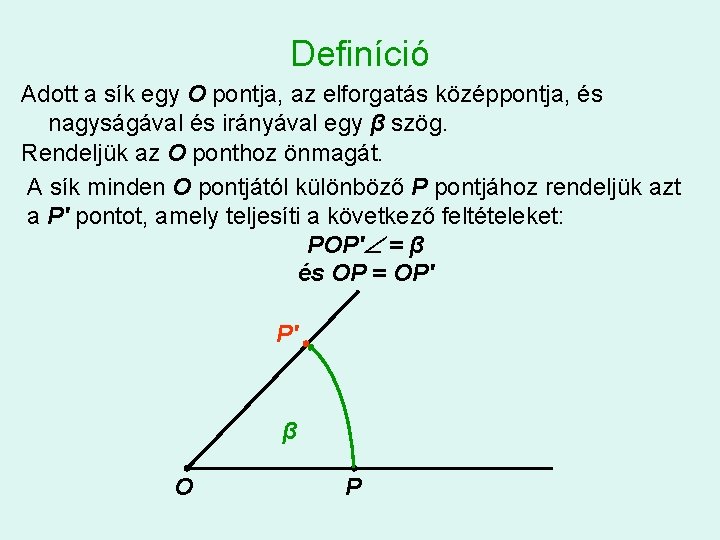
Definíció Adott a sík egy O pontja, az elforgatás középpontja, és nagyságával és irányával egy β szög. Rendeljük az O ponthoz önmagát. A sík minden O pontjától különböző P pontjához rendeljük azt a P' pontot, amely teljesíti a következő feltételeket: POP' = β és OP = OP' P' β O P

A pont körüli elforgatás tulajdonságai: 1. kölcsönösen egyértelmű, 2. általában nem szimmetrikus, 3. egyetlen fix pontja az O pont, ha csak az elforgatás szöge nem 0˚, 4. invariáns alakzat minden olyan kör, amelynek középpontja azonos az elforgatás középpontjával, 5. távolságtartó, 6. szögtartó, 7. a körüljárás irányát nem változtatja meg, 8. ha az elforgatás szöge 0˚, vagy 360˚, akkor az identitást kapjuk, azaz minden pont képe önmaga, 9. ha β = 180° (félfordulat), akkor a transzformáció a középpontos tükrözéssel azonos.

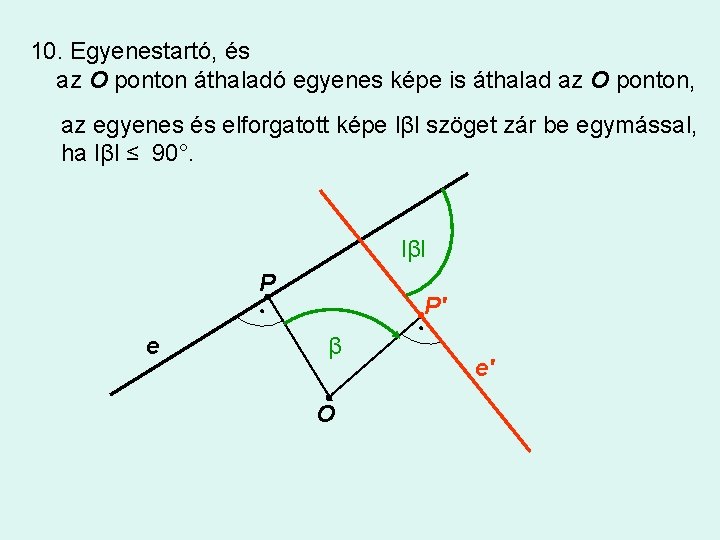
10. Egyenestartó, és az O ponton áthaladó egyenes képe is áthalad az O ponton, az egyenes és elforgatott képe lβl szöget zár be egymással, ha lβl ≤ 90°. lβl P e P' β O e'

Forgásszimmetria Definíció: egy alakzat forgásszimmetrikus, ha létezik olyan forgatás, amely az alakzatot önmagába viszi át.

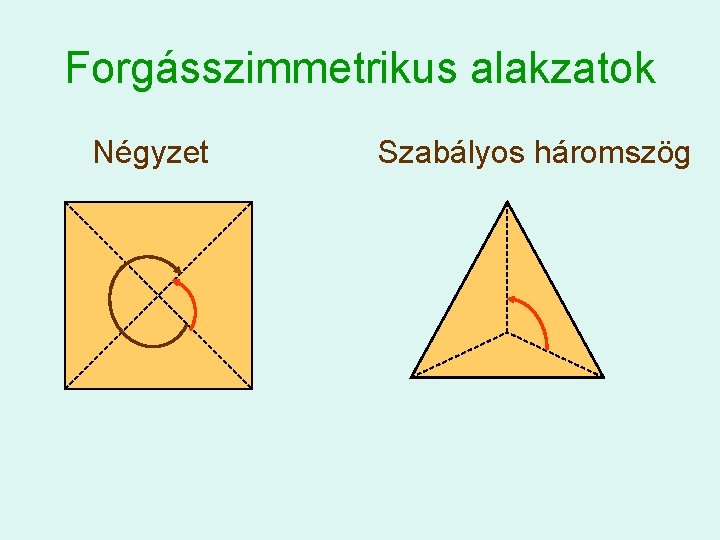
Forgásszimmetrikus alakzatok Négyzet Szabályos háromszög

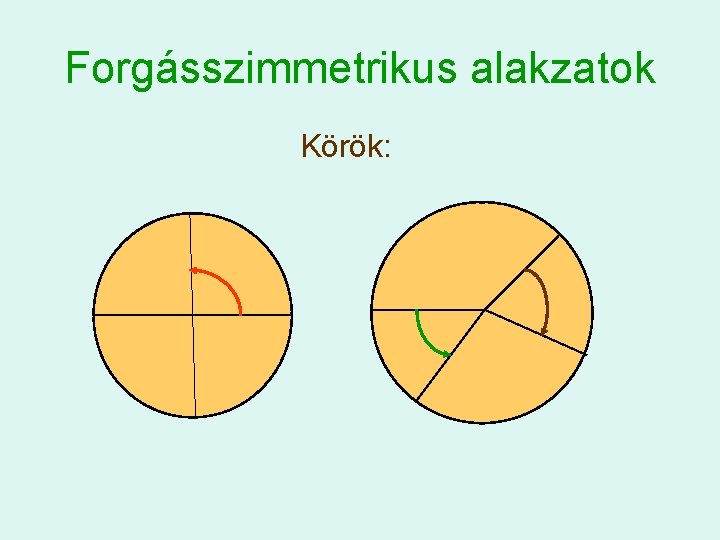
Forgásszimmetrikus alakzatok Körök:

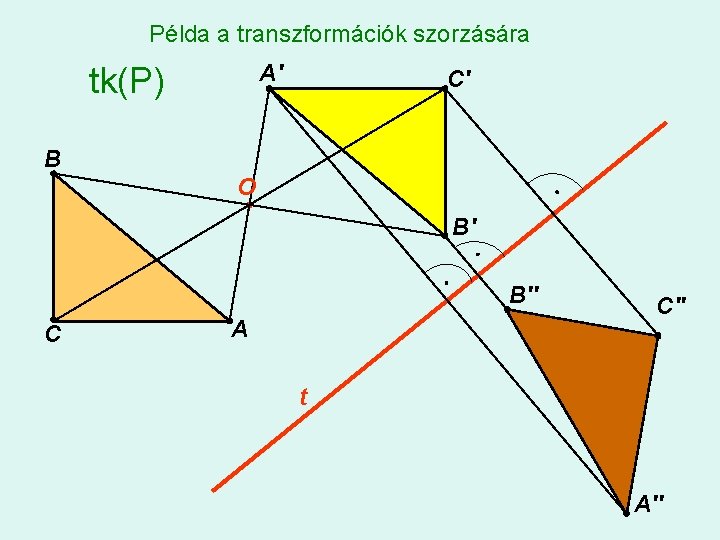
Transzformációk szorzata Definíció: két (vagy több) geometriai transzformációnak az egymás utáni elvégzését a két (vagy több) transzformáció szorzatának nevezzük. Jelölése: gf (P) Megjegyzés: a sorrendet a jobbról balra történő leolvasás adja meg.

Példa a transzformációk szorzására A' tk(P) C' B O B' B'' C A C'' t A''

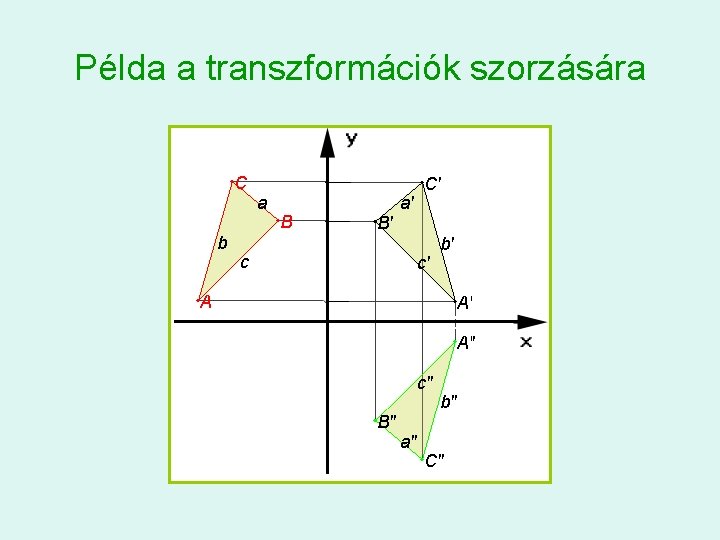
Példa a transzformációk szorzására

Egybevágósági transzformációk Definíció: a távolságtartó transzformációkat nevezzük egybevágósági transzformációknak.

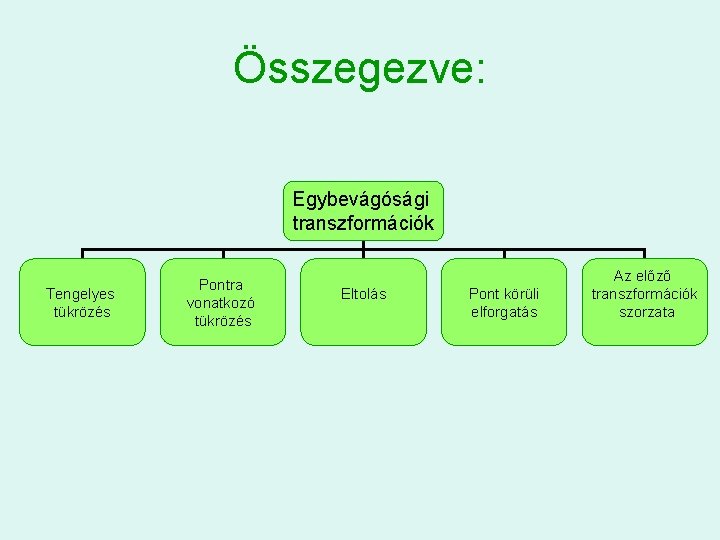
Összegezve: Egybevágósági transzformációk Tengelyes tükrözés Pontra vonatkozó tükrözés Eltolás Pont körüli elforgatás Az előző transzformációk szorzata

Alakzatok egybevágósága Definíció: egybevágónak nevezünk két alakzatot, ha van olyan távolságtartó transzformáció, amely az egyik alakzatot a másik alakzatba viszi át. Jele: Két azonos sugarú kör mindig egybevágó.

Háromszögek egybevágósága Két háromszög egybevágó, ha rájuk a következő feltételek egyike teljesül: 1. oldalaik hossza páronként megegyezik; 2. két-két oldal hossza páronként egyenlő, és az ezek által bezárt szögek egyenlők;

3. egy-egy oldaluk hossza és a rajtuk fekvő két szögük páronként egyenlő; 4. két-két oldaluk hossza páronként egyenlő, és a két-két oldal közül a hosszabbal szemközti szögek egyenlők.

Sokszögek egybevágósága Két sokszög egybevágó, ha rájuk a következő feltételek egyike teljesül: 1. megfelelő oldalaik hossza és megfelelő átlóik hossza egyenlő; 2. megfelelő oldalaik hossza és megfelelő szögeik páronként egyenlők.