2 Koordintarendszerek s transzformcik 2 1 Koordintarendszereink 2

2. Koordináta-rendszerek és transzformációk 2. 1. Koordináta-rendszereink 2. 2. Az egyenes és sík egyenlete 2. 3. Az E. tér projektív lezárása 2. 4. Affin transzformációk 2. 5. Projektív transzformációk

2. 2. Az egyenes és a sík egyenlete • Ebben a fejezetben az egyenes és a sík egyenletének különféle alakjait tárgyaljuk

Mire kell az analitikus geometria? • Geometriai modell: pontok, vonalak, felületek és testek tárolása (reprezentációja) • Átalakítások: geometriai számítások transzformációk • Rajzolás: geometrikus képek; vetületek - transzformációk

Egy alakzat egyenlete … (1) • 3 x + 4 y = 6 : egyenes egyenlete; – egyenlőség, – az egyenes pontjaira =, másra nem • ax + by + c = 0: az egyenes (általános) egyenlete; – paraméteres egyenlőség, – minden (a, b, c)-re egyenes egyenlete, – és minden egyeneshez van ilyen (a, b, c) • De nem minden egyeneshez van (m, b) : y = m x + b !

Egy alakzat egyenlete …(2) • ax + by + c < 0 : egy félsík egyenlőtlensége • y = f( x ), z = g( x, y ) : explicit (kifejezett) egyenletek • h( x, y ) = 0, pl. x 2 + y 2 -1 = 0 : implicit egyenlet • x = u( t ), y = v( t ); a t b pl. : paraméteres egyenletrendszer x = r ∙ cos t, y = r ∙ sin t, z = v ∙ t ; 0 t < T

2. 2. 1. Egyenesek egyenlete (E 2, 3) hogyan adjuk meg? hogyan tároljuk? honnan tudjuk, hogy az egyenes? hogyan számolunk vele?

Geometriai alapismeretek (ti) • (E 23) 2 pont egyértelműen meghatároz egyenest • (E 2? ) 1 pont és egy vektor egyértelműen meghatároz egyenest – (E 2) normálvektorként, illetve – (E 23) Irányvektorként • (E 3) 3 pont egyértelműen meghatároz egy síkot • (E 3) Ha n ┴ S (sík), akkor minden e S-re n ┴ e • (E 3) 1 pont és egy normálvektor egyértelműen meghatároz egy síkot • (E 3) 1 pont és két vektor egyértelműen meghatároz egy síkot, amely …

Két pontjával adott egyenes (E 2, 3) • Hogyan adhatjuk meg? (például) type Gxyz = real; // vagy double ? type Gpoint = record x, y [, z] : Gxyz; type Gline_pp = record P, Q end; : Gpoint; end; ------type Gvector = record 2009. 08 x, y [, z] : Gxyz; end; 8

[Két pontjával adott] egyenes paraméteres egyenlete • Adott: P = (px, py [, pz] ) és Q = (qx, qy [, qz] ); (E 2, 3) !!! • Az egyenes minden X pontjához van olyan t R hogy: X = P + t · (Q - P) = (1 - t) · P + t · Q ; - és minden t R –hez tartozik egy X PQ • Az összetevőkre hasonlóan: x = px + t · (qx – px), azaz: y = py + t · (qy – py), [ z = pz + t · (qz – pz), 2009. 08 x = (1 – t) · px + t · qx, y = (1 – t) · py + t · qy, z = (1 – t) · pz + t · qz ] 9

Egyenes pontjainak baricentrikus koordinátái • X = (1 - t) · P + t · Q • Az egyenes X pontjának baricentrikus koordinátái: t és 1 -t a P, Q alappontokra vonatkozóan;

t értéke a szakaszon és azon kívül Q X = (1 – t) · P + t · Q ; t>1 P 0<t<1 t<0 t=1 t=0 • egyenlőközű t értékek: egyenlőközű pontok, pl: t = 0, ¼, ½ ¾, 1 (! 2/4 -et nem ismeri) • t és (1 – t) : X baricentrikus koordinátái az egyenesen, a P, Q alappontokra vonatkozóan • a baricentrikus koordináták affin invariánsak !

Példa: egyenes metszése szakasszal (E 2 ): • Két egyenes metszéspontját számoljuk • és M a szakaszon van, ha 0 t 1

Az egyenes „irányvektoros” egyenlete (E 2, 3) • v = Q – P: az egyenes irányvektora • Ha adott P és v : X = P + t · v, x = px + t · vx , y = py + t · vy , [ z = pz + t · v]

Példa: két egyenes metszéspontja (E 2) – Adott egyenes P = (px, py) és Q = (qx, qy) pontjával – Adott egy másik; – metszéspontjuk: 2009. 08 R = (rx, ry) és S = (sx, sy) pontjával M = (mx, my) = (? , ? ) 14

Példa: két egyenes metszéspontja (E 2) PQ: M = P + t · (Q - P); t=? RS: M = R + t’· (S - R) t’ = ? PQ: mx = px + t · (qx - px); RS: mx = rx + t’· (sx - rx) my = py + t · (qy - py) my = ry + t’· (sy - ry) [mx = ] px + t · (qx - px) = rx + t’· (sx - rx) [mx = ] py + t · (qy - py) = ry + t’· (sy - ry) Ezekből t’ -t kiküszöbölve: t=…, majd ezzel mx = …, és my = … ? Mindig van megoldás? 15

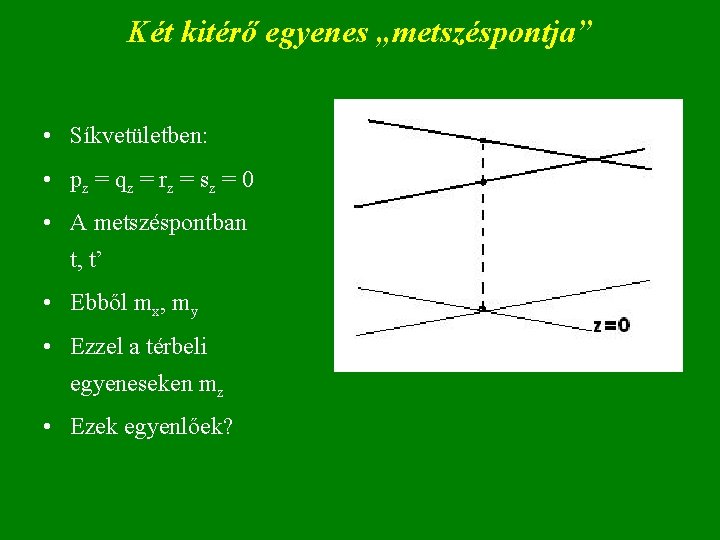
Példa: két egyenes metszéspontja (E 2, 3) – A síkban: 4 egyenlet, 4 ismeretlen: mx, my, t, t’; mx = px + t · (qx - px); mx = rx + t’· (sx - rx) my = py + t · (qy - py) my = ry + t’· (sy - ry) – Nincs megoldás, ha PQ || RS, vagy PQ = RS (det. = 0) – A térben: +1 ismeretlen: mz és +2 egyenlet (!!): mz = pz + t · (qz - pz) mz = rz + t’· (sz - rz) – Az egyenesek a térben lehetnek kitérőek ! – Megoldás: először egy síkvetületben oldjuk meg, pl. z = 0 ezzel kapunk: t és t’ ezzel kiszámítjuk a két egyenesen a z-t 2009. 08 16

Két kitérő egyenes „metszéspontja” • Síkvetületben: • pz = qz = rz = sz = 0 • A metszéspontban t, t’ • Ebből mx, my • Ezzel a térbeli egyeneseken mz • Ezek egyenlőek?

Példa: egyenes metszése szakasszal (E 2 ): • Két egyenes metszéspontját számoljuk • és M a szakaszon van, 0 t 1

Az egyenes normálegyenlete a síkban (E 2 !!! ) és ennek változatai

pontjával és normálisával adott egyenes (E 2) • Hogyan adjuk meg? • type Gline_np = record P : Gpoint; n : Gvector, end;

Az egyenes normál-egyenlete (E 2) • Adott P = (px, py) és n = (nx, ny) Az egyenesen bármely X = (x, y) pontra: ( X – P ) · n = 0, azaz: (x - px) · nx + (y - py) · ny = 0, • Az egyenesen ( X – P ) · n = 0 egyik oldalán > 0, a másikon < 0. • Átrendezve: X·n=P·n azaz: x · nx + y · ny = px · nx + py · ny ( x·a +y·b +c=0)

Az egyenes homogén, implicit egyenlete (E 2) • Az egyenes minden X = (x, y) pontjára (E 2): a · x + b · y + c = 0; a 2 + b 2 0; (a, b) az egyenes egy normálvektora • Bármely ilyen (a, b, c) meghatároz egyenest, és bármely egyeneshez van ilyen (a, b, c) számhármas. • Az egyenlet „implicit” (nem explicit) és „homogén”: (a, b, c) · h; h 0

(a, b, c)-vel adott egyenes (E 2) • Hogyan adjuk meg? • type Gline_abc = record a, b, c : Gxyz; end;

A homogén, implicit egyenlet … (E 2) – olv. • Hesse-féle normál alakban : a’ · x + b’ · y + 1 = 0; a’ 2 +b’ 2 =1; (a’; b’) egy normál-egységvektor • Salmon féle alakban: x / a” + y / b” = 1 • Homogén koordinátákkal; az X = [x, y, w] pontokra (H 2): a · x + b · y + c · w = 0; a 2+b 2 0; • Egy egyenes megadása: [a, b, c] h ·[a, b, c]; a 2+b 2 0;

Az egyenes egyenlete determináns alakban (E 2 !!!) - olv • Adott: P = (px, py) és Q = (qx, qy) a síkban (!!!) • és egy tetszőleges X = (x, y) pontja d(PQX) = | x y 1 | = a háromszög területe x 2. | px py 1 | | qx qy 1 | • Ha P, Q, X egyenesbe esik, akkor: d(PQX) = 0, azaz (py - qy)x + (qx - px)y + (px qy - py qx) = 0

A determináns kifejtése (E 2) - t. i. • d(PQX) = | x y 1 | = x · D 11 – y · D 12 + 1 · D 13 = | px py 1 | | qx qy 1 | = x · (py - qy) – y · (px - qx) + 1 · (px · qy - py · qx)

Az egyenes iskolai „egyenlete” (E 2) • y = M · x + B; csak korlátozottan használható; • az x = c egyenesekre nem !!! Kerüljük, • Így használható: adott P 1 = (y 1, y 1) és P 2=(x 2, y 2) pontján át: (x 2 – x 1) · (y – y 1) = (y 2 – y 1) · (x – x 1)

Félsík megadása (E 2) • (1) Homogén lineáris egyenlőtlenséggel: a · x + b · y + c < 0; a 2 + b 2 0; • (2) a határ-egyenese: (R, n) „normál-egyenlőtlensége”: ( X – R ) · n < 0, a félsík minden X pontjára n R R

2. 2. 2. Síkok egyenlete (E 3)

A sík paraméteres egyenlete ( E 3)

Három pontjával adott sík • Hogyan adjuk meg? • Például: type Gplane_ppp = record P, Q, R : Gpoint; end;

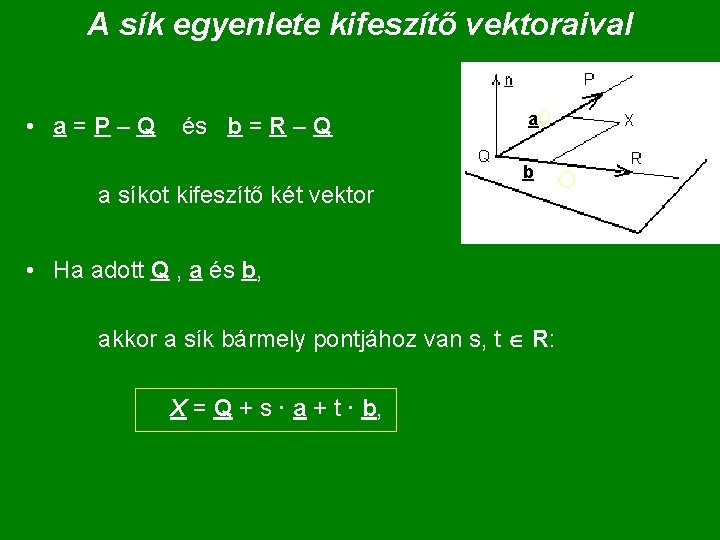
A sík egyenlete kifeszítő vektoraival • a=P–Q és b = R – Q a síkot kifeszítő két vektor a b • Ha adott Q , a és b, akkor a sík bármely pontjához van s, t R: X = Q + s · a + t · b,

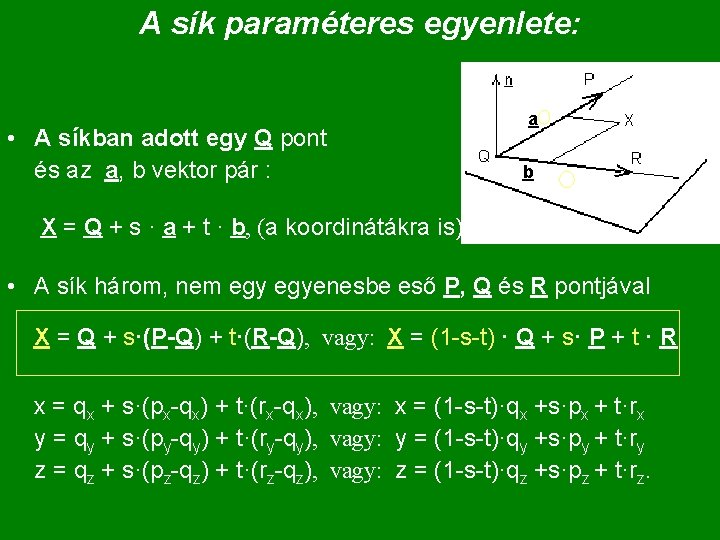
A sík paraméteres egyenlete: • A síkban adott egy Q pont és az a, b vektor pár : a b X = Q + s · a + t · b, (a koordinátákra is) • A sík három, nem egyenesbe eső P, Q és R pontjával X = Q + s·(P-Q) + t·(R-Q), vagy: X = (1 -s-t) · Q + s· P + t · R x = qx + s·(px-qx) + t·(rx-qx), vagy: x = (1 -s-t)·qx +s·px + t·rx y = qy + s·(py-qy) + t·(ry-qy), vagy: y = (1 -s-t)·qy +s·py + t·ry z = qz + s·(pz-qz) + t·(rz-qz), vagy: z = (1 -s-t)·qz +s·pz + t·rz.

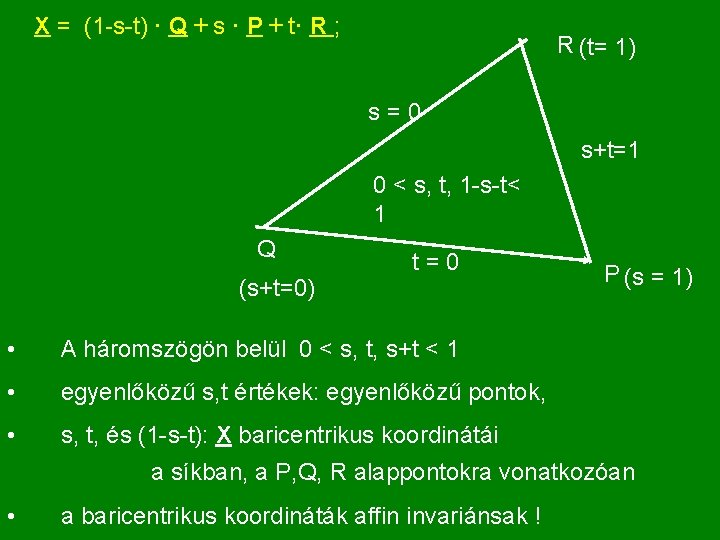
A sík paraméteres egyenlete: X = Q + s·(P - Q) + t·(R - Q), vagy: X = (1 -s-t)·Q + s·P + v·R ha 0 s, t, 1 -s-t 1 : a háromszög pontjai, ha egyik nulla: a háromszög egyik oldala, ha kettő nulla (és a harmadik 1): egyik csúcsa, ha valamelyik negatív, vagy >1: a pont kívül van. s, t, 1 -s-t : baricentrikus koordináták a síkban [ jó észrevenni: 0 1 -s-t 1 acsaha 0 s+t 1 ]

X = (1 -s-t) · Q + s · P + t· R ; R (t= 1) s=0 s+t=1 0 < s, t, 1 -s-t< 1 Q (s+t=0) t=0 • A háromszögön belül 0 < s, t, s+t < 1 • egyenlőközű s, t értékek: egyenlőközű pontok, • s, t, és (1 -s-t): X baricentrikus koordinátái P (s = 1) a síkban, a P, Q, R alappontokra vonatkozóan • a baricentrikus koordináták affin invariánsak !

Példa: egyenes döféspontja síkkal – A döféspontot jelöljük így: M = (x, y, z ) – A PQR síkjának egyenlete: M = (1 -s-t) · Q + s · P + t · R ; az ST egyenes egyenlete: M = (1 -w) · S + w · T ; – A 3+3 egyenlet, 6 ismeretlen: x, y, z, s, t, w; – Megoldás: az M két kifejezése egyenlő egymással. Marad 3 egyenlet az s, t, w ismeretlenekre – De az egyenes és sík lehetnek párhuzamosak !

A sík normálegyenlete és annak változatai (E 3)

pontjával és normálisával adott sík • Hogyan adjuk meg? • Például: type Gplane_np = record P : Gpoint; n : Gvector, end;

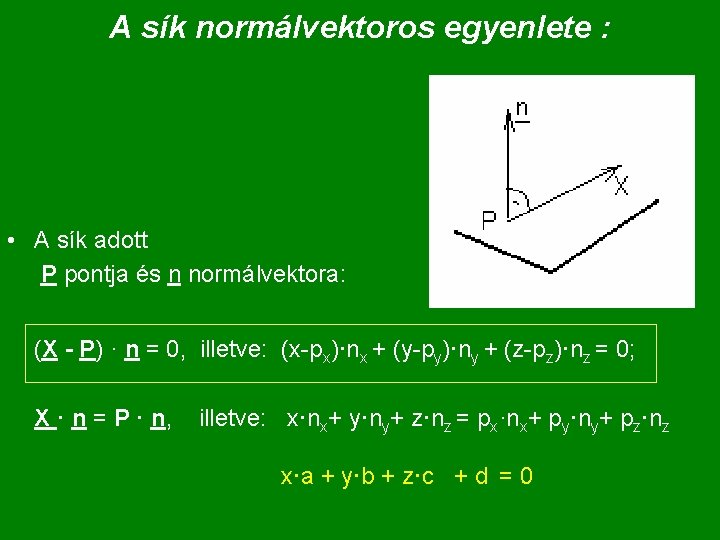
A sík normálvektoros egyenlete : • A sík adott P pontja és n normálvektora: (X - P) · n = 0, illetve: (x-px)·nx + (y-py)·ny + (z-pz)·nz = 0; X · n = P · n, illetve: x·nx+ y·ny+ z·nz = px·nx+ py·ny+ pz·nz x·a + y·b + z·c + d = 0

A sík implicit, homogén egyenlete • A sík homogén, implicit egyenlete: a · x + b · y + c · z + d = 0; a 2 + b 2 + c 2 0 Egy sík megadása (tárolása): [a, b, c]; a 2 + b 2 + c 2 0

A sík implicit, homogén egyenlete - olv a·x + b·y + c·z + d = 0; a 2+b 2+c 2 0 • Hesse-féle normálalak: a’·x+b’·y+c’·z+d’=0; a’ 2+b’ 2+c’ 2=1 • Salmon féle alak: x / a” + y / b” + z / c” = 1 • determináns alak: 3 nem egyenesbe esően adott pont, P = (px, py, , pz, ), Q = (qx, qy, qz, ), R = (rx, ry, rz, ): | | x px qx rx y py qy ry z pz qz rz 1 1 | = 0 | | | (az első sor szerint kifejtve …) (Az X, P, Q, R tetraéder térfogatának 6 -szorosa. )

A determináns kifejtése (E 3) - t. i. • | | x px qx rx y py qy ry z pz qz rz 1 1 | = 0 | | | (az első sor szerint kifejtve …) • d(PQRX) = (az első sor szerint kifejtve …) = | | x px qx rx y py qy ry z pz qz rz 1 1 | | = = x · D 11 – y · D 12 + z · D 13 - 1 · D 14 és pl. : D 11 = py · (qz - rz) – pz · (qy - ry) + 1 · (qy · rz - qz · ry )

Lássunk a koordináták mögé – t. i. • z = 0; mi ez? Egyenlőség, egyenlet, kié-mié? 0 x+0 y+1 z+0=0 sík: z = 0 és akármilyen x, y; az XY sík • x + y = 0 mi az? HF !

További példák …

Egyenes döféspontja háromszöggel (E 3): t. i. • Adott egy háromszög A, B, C csúcsai, síkjának egyenlete: X = B + s · (A - B) + t · (C - B) • Adott egyenes P, Q pontjaival. az egyenes egyenlete: X = P + u · (Q - P). • döféspont: [ X = ] B + s · (A - B) + t · (C - B) = P + u · (Q - P) • 3 egyenlet; 3 ismeretlen: t, s, u; ezekből számolható X. • Ha 0 s, t, 1 -s-t 1, akkor X a háromszögben van. • (Nincs megoldás: párhuzamosak, vagy egybe esnek. )

Áttérés egy másik egyenletre – t. i. • Adott (a, b, c): a · x + b · y + c · z + d = 0 • Írjuk föl a normál egyenletét: (X – R) · n = 0 • Ehhez kell egy R pontja és egy n normálisa. • a, b, c nem mind 0, ezért lehet R = (-d / a, 0, 0), vagy: (0, -d / b, 0), vagy (0, 0, -d / c) • és egy n : = (a, b, c);

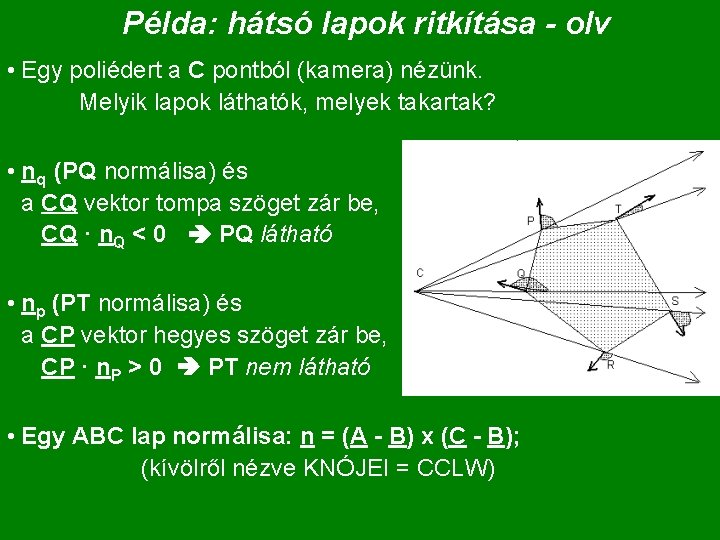
Példa: hátsó lapok ritkítása - olv • Egy poliédert a C pontból (kamera) nézünk. Melyik lapok láthatók, melyek takartak? • nq (PQ normálisa) és a CQ vektor tompa szöget zár be, CQ · n. Q < 0 PQ látható • np (PT normálisa) és a CP vektor hegyes szöget zár be, CP · n. P > 0 PT nem látható • Egy ABC lap normálisa: n = (A - B) x (C - B); (kívölről nézve KNÓJEI = CCLW)