1 5 Delta Function Function Spaces Christopher Crawford










- Slides: 11

§ 1. 5 Delta Function; Function Spaces Christopher Crawford PHY 416 2014 -09 -24

Outline • Example derivatives with singularities Electric field of a point charge – divergence singularity Magnetic field of a line current – curl singularity • Delta singularity δ(x) Motivation – Newton’s law: yank = mass x jerk Definition – differential of step function dϑ = δ dx Important integral identities Calculating with delta functions • Distributions – vs. functions Delta as an `undistribution’ Singularities and boundary conditions Building up higher dimensions: δ 3(r) • Linear function spaces – functions as vectors Delta as a basis function or identity operator Correspondence table between vectors and functions 2

Example: magnetic field of a straight wire • This time: a singularity in the curl of magnetic intensity (flow) 3

Example: Inverse Square Law • Force of a constant carrier flux emanating from a point source 4

Newton’s law • yank = mass x jerk • force = mass x accel. • impulse = m x Δv singularities become more pronounced! 5

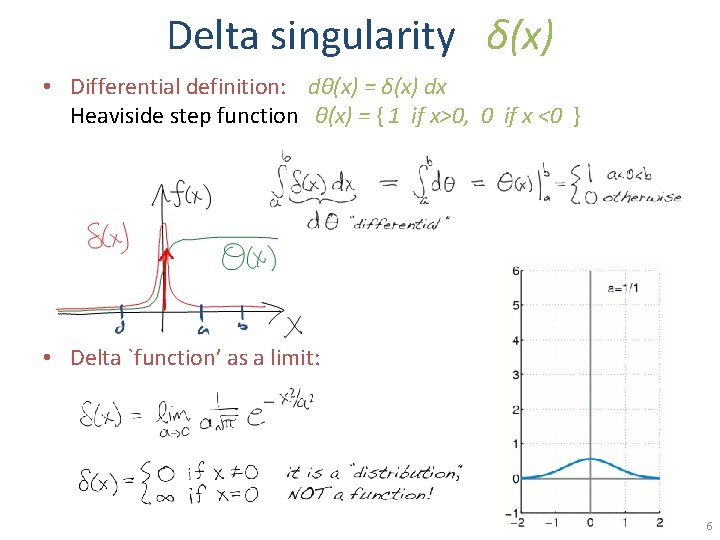
Delta singularity δ(x) • Differential definition: dϑ(x) = δ(x) dx Heaviside step function ϑ(x) = { 1 if x>0, 0 if x <0 } • Delta `function’ as a limit: 6

Important integral identities • Note the different orders of derivative • Offset delta function 7

Calculations with δ(x) • Jacobian • Higher dimension 8

Delta `undistribution’ • Something you can integrate (a density) – The “distribution” of mass or charge in space • The delta `function’ is not well defined as a function – but it is perfectly meaningful as an integral • Think of δ(x) as an “undistribution” – The charge is clumped up into a singularity 9

Boundary conditions • 2 -d version of a PDE on the boundary • Derived from PDE by integrating across the boundary • RULES: • Proof: 10

δ(x) as a basis function • Each f(x) is a component for each x – Write function as linear combination • δ(x’) picks off component f(x) • The Dirac δ(x) is the continuous version of Kröneker δij – Represents a continuous type of “orthonormality” of basis functions • It is the kernel (matrix elements) of the identity matrix 11