1 4 The Extreme Point Theorem Geometry of

  • Slides: 7
Download presentation
1. 4 The Extreme Point Theorem : Geometry of a linear programming problem §

1. 4 The Extreme Point Theorem : Geometry of a linear programming problem § The set of feasible solutions to a general linear programming problem is a convex polyhedron. ref. Convex Polytopes, by Branko Grünbaum, 1967 & 2003

Extreme point (of a convex set S ) • a point in S which

Extreme point (of a convex set S ) • a point in S which does not lie in any open line segment joining two points of S Krein–Milman theorem If S is convex and compact in a locally convex space, then S is the convex hull of its extreme points. A convex set in light blue, and its extreme points in red. => Given a convex shape K (light blue) and its set of extreme points B (red), the convex hull of B is K.

§ Theorem 1. 5. (85 p) The set of all convex combinations of a

§ Theorem 1. 5. (85 p) The set of all convex combinations of a finite set of points in R^n is a convex set § Therorem 1. 6. (86 p) Let S be a convex set in R^n. A point u in S is an extreme point of S if and only if u is not a convex combination of other points of S.

§ If a linear programming problem has an optimal solution, then this solution must

§ If a linear programming problem has an optimal solution, then this solution must occur at an extreme point. § The set pf all feasible solutions to a general linear programming problem contains an infinite number of points. § But there are only a finite number of extreme points, but this number may be very large.

§ THEOREM 1. 7 (EXTREME POINT). Let S be the set of feasible solutions

§ THEOREM 1. 7 (EXTREME POINT). Let S be the set of feasible solutions to a general linear programming problem. 1. If S is nonempty and bounded, then an optimal solution to the problem exists and occurs at an extreme point. 2. If S is nonempty and not bounded and if an optimal solution to the problem exists, then an optimal solution occurs at an extreme point. 3. If an optimal solution to the problem does not exist, then either S is empty or S is unbounded.

§ The convex set of all feasible solutions consists of the points that lie

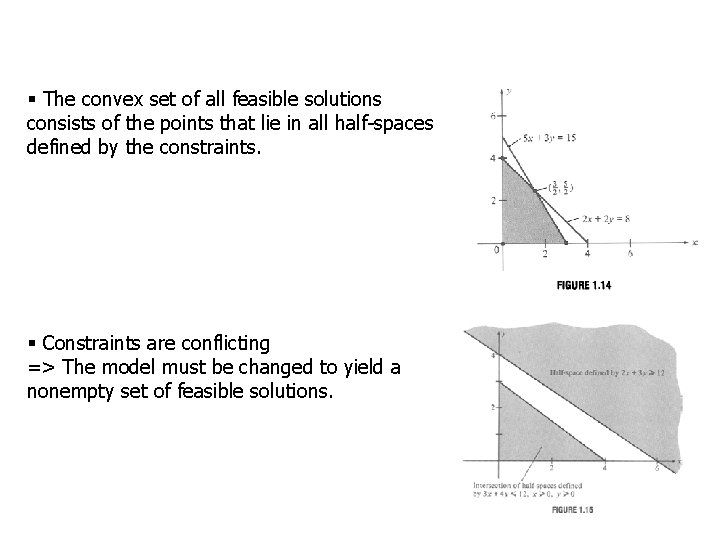
§ The convex set of all feasible solutions consists of the points that lie in all half-spaces defined by the constraints. § Constraints are conflicting => The model must be changed to yield a nonempty set of feasible solutions.

references • • • http: //en. wikipedia. org/wiki/Convex_polyhedron http: //mathworld. wolfram. com/Convex. Polyhedron. html

references • • • http: //en. wikipedia. org/wiki/Convex_polyhedron http: //mathworld. wolfram. com/Convex. Polyhedron. html http: //en. wikipedia. org/wiki/Extreme_point http: //en. wikipedia. org/wiki/Krein%E 2%80%93 Milman_theorem http: //library. wolfram. com/infocenter/Math. Source/440/ http: //www. ifor. math. ethz. ch/~fukuda/fukuda. html V 2008122 Lee, Young Min

Projective Geometry Projective Geometry Projective Geometry Projective GeometryProjective Geometry Projective Geometry Projective Geometry Projective Geometry
EXTREME SPORTS Bungee jumping Extreme mountain biking ExtremeEXTREME SPORTS Bungee jumping Extreme mountain biking Extreme
EXTREME COLD AND EXTREME HEAT EXTREME COLD HumansEXTREME COLD AND EXTREME HEAT EXTREME COLD Humans
ROLLES THEOREM AND THE EXTREME VALUE THEOREM SectionROLLES THEOREM AND THE EXTREME VALUE THEOREM Section
SHAPE SPACE Pythagorean Theorem Pythagorean Theorem Pythagorean TheoremSHAPE SPACE Pythagorean Theorem Pythagorean Theorem Pythagorean Theorem
LEMIs Theorem Lamis Theorem Statement Lamis theorem isLEMIs Theorem Lamis Theorem Statement Lamis theorem is