Year 9 Ratio Proportion Dr J Frost jfrosttiffin

Year 9: Ratio & Proportion Dr J Frost (jfrost@tiffin. kingston. sch. uk) www. drfrostmaths. com Last modified: 10 th September 2015

Starter Puzzles 1 (You can work in pairs) 3 ? ? N 2 ? ?

Direct Proportion Iain wants to make a Baked Alaska. He requires 24 eggs to make 700 g of the pudding. How many eggs does he require to make 1250 g? Method 1: Unitary Method ? Method 2: Ratio Method We say that the number of eggs and the mass of the pudding are ‘directly proportional’. There is some underlying ‘scaling’ between the two things.

Test Your Understanding Solve the following using both the ‘unitary method’ (i. e. find quantity for one unit) and the ‘ratio method’. The mass of 16 cm 3 of Neoginium is 24 g. What is the mass of Q 20 cm 3 of the same element? Unitary Method Ratio Method ? ? If you finish: Q ?

Direct Proportion ! Two things are directly proportional if they in the same ratio. Can you suggest variables that might be directly proportional? • Speed and distance travelled (if you double your speed, you double the distance travelled). • Total cost and quantity purchased. ? • Length of steel rod and weight. Why is “hours revised for maths exam” and “maths exam mark” not likely to be directly proportional? If we 5 hours revision resulted in 60%, then clearly 10 hours revision wouldn’t result in 120%! So while the two ? things are ‘correlated’, they are not directly proportional. Q Electricity cost is directly proportional to the hours of TV watched. If 2 hours are watched, a cost of 14 p is incurred. If 7 hours is watched, what cost is incurred? ?

Exercise 1 (see provided sheet) 5 If it takes 3 men 5 hours to dig 12 holes, how 1 many hours does it take for 3 men to dig 84 holes? 35 hours ? ? 6 [IMC 2009 Q 9] Joseph’s flock has 55% more sheep than goats. What is the ratio of goats to sheep in the flock? A 9: 11 B 20: 31 C 11: 20 D 5: 9 E 9: 20 Solution: B 2 ? ? 7 [IMC 2005 Q 6] A shop advertise ‘Buy one, get 3 ? ? ? 4 one at half price’. For this offer, the average cost per item is the same as: A Two for the price of one B Three for the price of one C Three for the price of 2. D Four for the price of three E Five for the price of four Solution: D (make the original cost of each item £ 1 for simplicity, and go from there) ? ?

Exercise 1 (see provided sheet) N 8 ? N ? ? 9 N ? ?

Inverse Proportion Suppose Mo runs at a speed of 8 m/s for second, and takes 120 seconds to finish. If he ran double the speed at 16 m/s, what happens to his time? It halves! ? And what do you notice about the speed multiplied by the time in the two cases? It remains the ? same. ! When two quantities are inversely (or ‘indirectly’) proportional, their product remains constant.

Example Q Four bricklayers can build a certain wall in ten days. How long would it take five bricklayers to build it? Method 1: Constant Product Method 2: Unitary Method Find how many days one bricklayer would take! ? ? days. 4 bricklayers take 10 1 bricklayer takes 40 days 5 bricklayers take 8 days

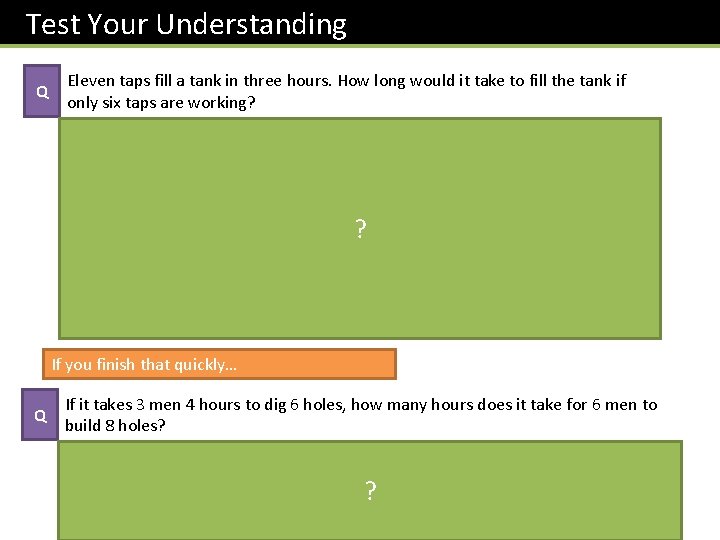
Test Your Understanding Q Eleven taps fill a tank in three hours. How long would it take to fill the tank if only six taps are working? ? If you finish that quickly… Q If it takes 3 men 4 hours to dig 6 holes, how many hours does it take for 6 men to build 8 holes? Notice that “men” and “hours” are inversely 3 men 4 hours for 6 holes proportional but “hours” and “holes” are directly 6 men 2 hours for 6 holes ? proportional. 6 men 1/3 hours for 1 holes 6 men 8/3 hours for 8 holes (which is 2 hours 40 minutes)

Exercise 2 6 1 ? ? 2 7 ? 3 ? ? 4 8 ? 5 ? ?