Where Mathematics meets the Internet Teletraffic theory mathematics

Where Mathematics meets the Internet • Teletraffic theory: mathematics applicable to the design, control and management of the PSTN. • Activities: statistical inference, mathematical modeling, optimization, queueing and performance analysis. • Extends to the Internet: • Internet Engineering: design, management, control and operations of the global Internet. • But not a good mapping!!! 1

Where Mathematics meets the Internet • Vast difference in Qo. S requirements and expectations. • PSTN: highly static nature, limited variability. • Can accurately model the behavior and impact of single and aggregate users. • Poisson call arrival process, exponentially distributed hold times. • Results in a parsimonious traffic model (i. e. , one that accurately reflects actual systems with few parameters). • Key change to PSTN: Use of data playing havoc with existing PSTN infrastructure. • For data networks, Poisson models totally miss the observed burstiness of data networks. 2

Where Mathematics meets the Internet • Data traffic is highly bursty…. . • This term is intuitively understood…but difficult to nail down a precise mathematical meaning. • The time scale is a major component of the definition: the time scale over which activities and lulls occur. • For telephony, the time scale is tied to the Lambda param of the Poisson process. • E. g. lambda=100/sec implies the time scale of interest is 10 ms as periods of greater than average activity over larger time scales (or lower times scales) occur with rapidly diminishing probability. • Data networks exhibit burstiness on many different time scales. • The Poisson framework does not even have provide a vocabulary for discussing burstiness of this sort. • Data traffic has been described as ‘traffic spikes that ride on longer-term ripples, that in turn ride on still longer-term swells’ [Fowler and Leland, “Local Area Network Traffic Characteristics for Broadband Network Congestion Mangement”]. 3

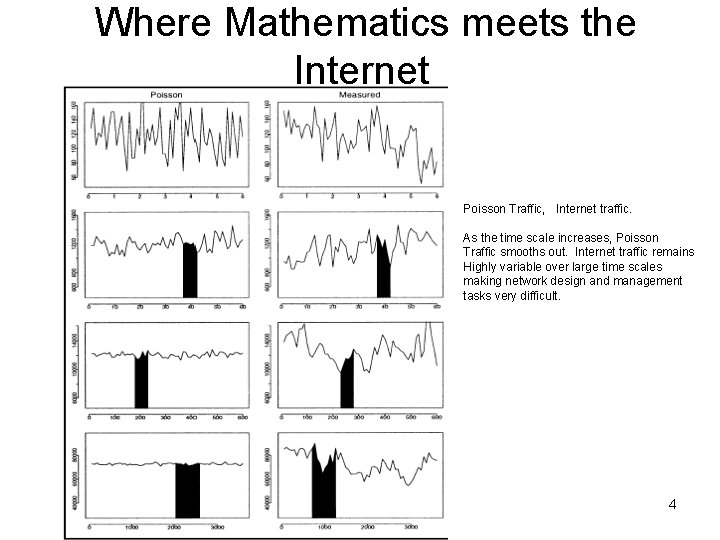
Where Mathematics meets the Internet Poisson Traffic, Internet traffic. As the time scale increases, Poisson Traffic smooths out. Internet traffic remains Highly variable over large time scales making network design and management tasks very difficult. 4

Where Mathematics meets the Internet • As the time scale increases, the Poisson traffic ‘smooths out’ which can be easily engineered for. • Bursty data traffic requires routers to have large buffers, networks must be highly over-provisioned in order to avoid poor performance. 5

Where Mathematics meets the Internet • The mathematics for POTS is one of limited variability: • Time: traffic processes are either independent or have temporal correlations that decay exponentially fast. • Space: distributions of traffic-related quantities have exponentially decaying tails. • For Data Networks the mathematics must convey extreme variability (e. g. , long-range dependence. • Time: the autocorrelation exhibits power-law decay. 6

Where Mathematics meets the Internet • Extreme spatial variability can be described parsimoniously using heavytailed distributions with infinite variance, i. e. , probability distributions F with the property that for large x values, Where Beta is in the interval (0, 2) Simplest heavy-tailed distribution is Pareto Infinite mean Infinite variance 7

Where Mathematics meets the Internet 8

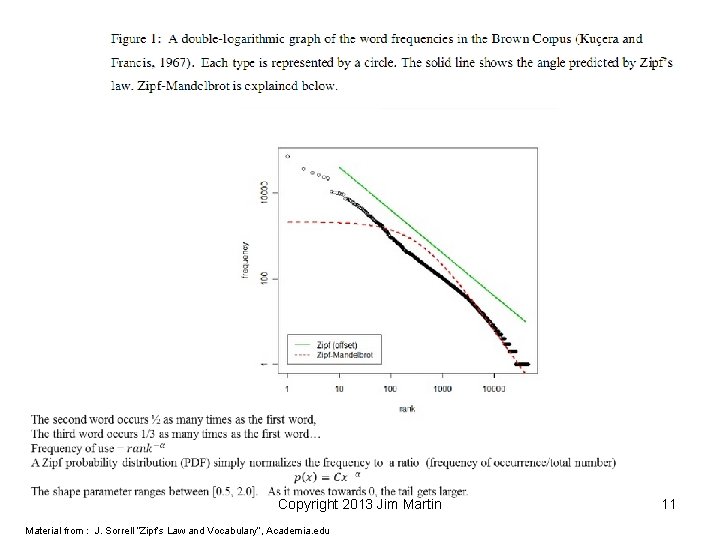
Zipf’s Law • Developed by George Zipf in early 1900’s to describe the ‘frequency of use’ of words in the English Language – Rank order the ‘popularity’ of every word • Zipf’s Law – the size of the r’th ranked occurance is inversely proportional to its rank Copyright 2013 Jim Martin 9

Copyright 2013 Jim Martin Material from : J. Sorrell “Zipf’s Law and Vocabulary”, Academia. edu 10

Copyright 2013 Jim Martin Material from : J. Sorrell “Zipf’s Law and Vocabulary”, Academia. edu 11

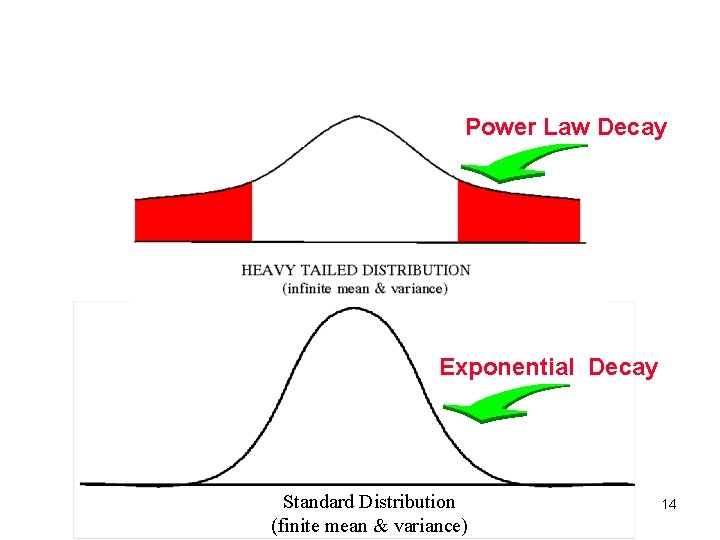
Heavy-Tailed Distributions • … infinite variance … infinite mean • Introduced by Pareto in the 1920’s • --- “probabilistic curiosity. ” • Mandelbrot established the use of heavy-tailed distributions to model realworld fractal phenomena. • Examples: stock-market, earth-quakes, weather, . . . 12

Decay of Distributions • Standard --- Exponential Decay • e. g. Normal: • • Heavy-Tailed --- Power Law Decay • e. g. Pareto-Levy: • • 13

Power Law Decay Exponential Decay Standard Distribution (finite mean & variance) 14

How to Check for “Heavy Tails”? • Log-Log plot of tail of distribution • should be approximately linear. • Slope gives value of • infinite mean and infinite variance • infinite variance 15

Where Mathematics meets the Internet • Network traffic has been shown to be self-similar: • An object whose appearance is unchanged regardless of the scale at which it is viewed. • A self similar process can exhibit long-range dependence. • Fundamental cause: heavy-tailed nature associated with human/computer interaction: • Files sizes • Human behaviors drive on times and off times 16