Vector Mechanics For Engineers Statics Twelfth Edition Chapter

Vector Mechanics For Engineers: Statics Twelfth Edition Chapter 9 Distributed Forces: Moments of Inertia ©View Stock/Getty Images RF © 2019 Mc. Graw-Hill Education. All rights reserved. Authorized only for instructor use in the classroom. No reproduction or further distribution permitted without the prior written consent of Mc. Graw-Hill Education.

Contents Introduction Sample Problem 9. 6 Moments of Inertia of an Area Sample Problem 9. 7 Moment of Inertia of an Area by Integration Mohr’s Circle for Moments and Products of Inertia Polar Moment of Inertia Sample Problem 9. 8 Radius of Gyration of an Area Moment of Inertia of a Simple Mass Sample Problem 9. 1 Parallel Axis Theorem Sample Problem 9. 2 Moment of Inertia of Thin Plates Parallel Axis Theorem Moment of Inertia of a 3 D Body by Integration Moments of Inertia of Composite Areas Moment of Inertia of Common Geometric Shapes Sample Problem 9. 4 Sample Problem 9. 5 Product of Inertia Principal Axes and Principal Moments of Inertia © 2019 Mc. Graw-Hill Education. Sample Problem 9. 12 Mass Products of Inertias Principal Axes and Principal Moments of Inertia

Introduction We have previously considered distributed forces that were proportional to the area or volume over which they act. • The resultant was obtained by summing or integrating over the areas or volumes. • The moment of the resultant about any axis was determined by computing the first moments of the areas or volumes about that axis. We will now consider forces that are both proportional to the area or volume over which they act and also vary linearly with distance from a given axis. • It will be shown that the magnitude of the resultant depends on the first moment of the force distribution with respect to the axis. • The point of application of the resultant depends on the second moment of the distribution with respect to the axis. The current chapter will present methods for computing the second moment, or moment of inertia, for areas. © 2019 Mc. Graw-Hill Education.

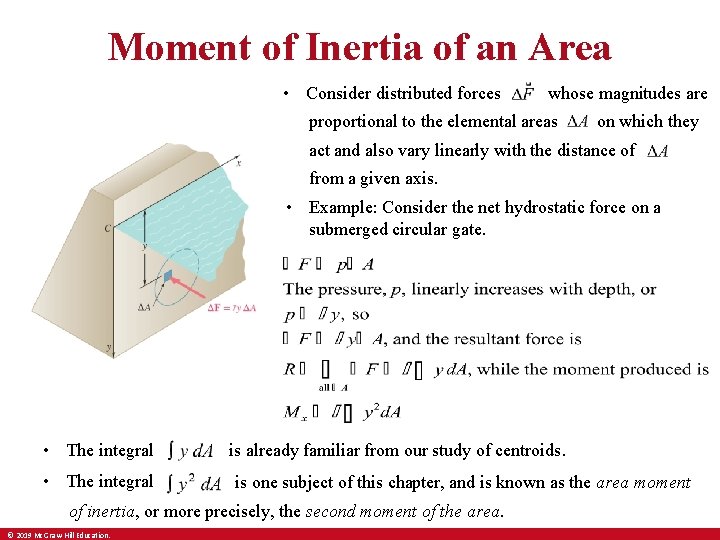
Moment of Inertia of an Area • Consider distributed forces whose magnitudes are proportional to the elemental areas on which they act and also vary linearly with the distance of from a given axis. • Example: Consider the net hydrostatic force on a submerged circular gate. • The integral is already familiar from our study of centroids. is one subject of this chapter, and is known as the area moment of inertia, or more precisely, the second moment of the area. © 2019 Mc. Graw-Hill Education.

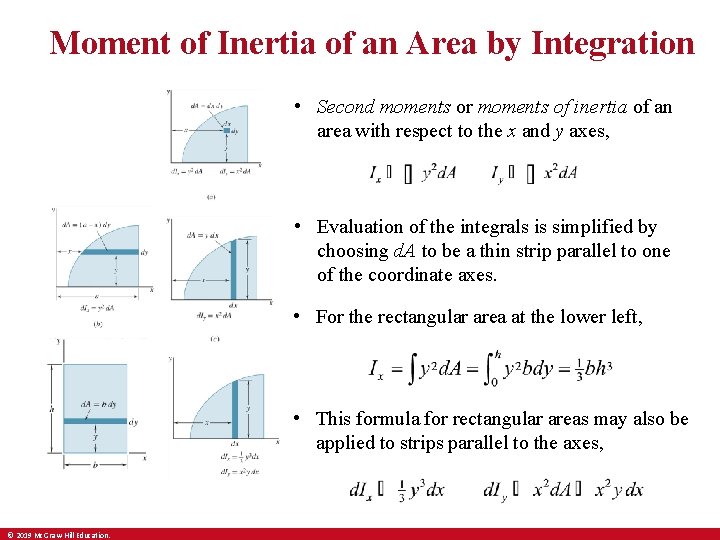
Moment of Inertia of an Area by Integration • Second moments or moments of inertia of an area with respect to the x and y axes, • Evaluation of the integrals is simplified by choosing d. A to be a thin strip parallel to one of the coordinate axes. • For the rectangular area at the lower left, • This formula for rectangular areas may also be applied to strips parallel to the axes, © 2019 Mc. Graw-Hill Education.

Polar Moment of Inertia • The polar moment of inertia is an important parameter in problems involving torsion of cylindrical shafts and rotations of slabs. • The polar moment of inertia is related to the rectangular moments of inertia, © 2019 Mc. Graw-Hill Education.

Radius of Gyration of an Area • Consider area A with moment of inertia Ix. Imagine that the area is concentrated in a thin strip parallel to the x axis, and has an equivalent Ix. kx = radius of gyration with respect to the x axis • Similarly, © 2019 Mc. Graw-Hill Education.

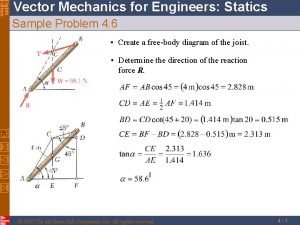
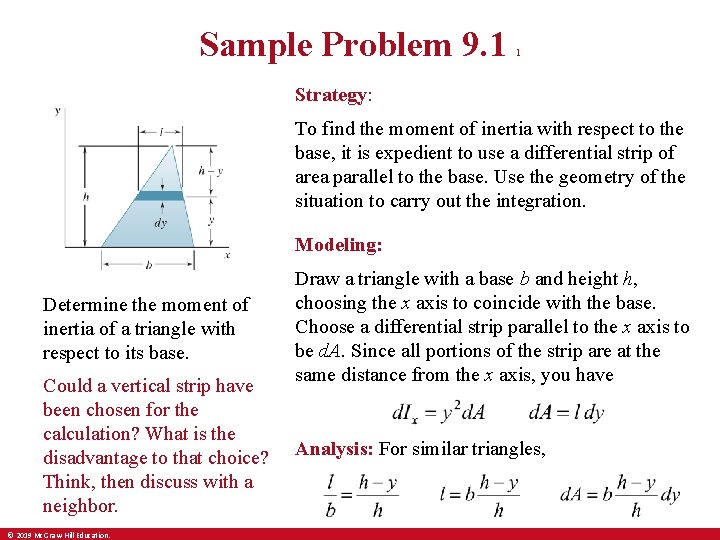
Sample Problem 9. 1 1 Strategy: To find the moment of inertia with respect to the base, it is expedient to use a differential strip of area parallel to the base. Use the geometry of the situation to carry out the integration. Modeling: Determine the moment of inertia of a triangle with respect to its base. Could a vertical strip have been chosen for the calculation? What is the disadvantage to that choice? Think, then discuss with a neighbor. © 2019 Mc. Graw-Hill Education. Draw a triangle with a base b and height h, choosing the x axis to coincide with the base. Choose a differential strip parallel to the x axis to be d. A. Since all portions of the strip are at the same distance from the x axis, you have Analysis: For similar triangles,

Sample Problem 9. 1 2 • Integrating d. Ix from y = 0 to y = h, Reflect and Think: This problem also could have been solved using a differential strip perpendicular to the base by applying Eq. (9. 2) to express the moment of inertia of this strip. However, because of the geometry of this triangle, you would need two integrals to complete the solution. © 2019 Mc. Graw-Hill Education.

Sample Problem 9. 2 1 Strategy: Since the area is circular, you can evaluate part (a) by using an annular differential area. For part (b), you can use symmetry and Eq. (9. 4) to solve for the moment of inertia with respect to a diameter. Modeling and Analysis: a) Determine the centroidal polar moment of inertia of a circular area by direct integration. b) Using the result of part a, determine the moment of inertia of a circular area with respect to a diameter of the area. © 2019 Mc. Graw-Hill Education. Why was an annular differential area chosen? Would a rectangular area have worked?

Sample Problem 9. 2 2 From symmetry, Ix = Iy, Reflect and Think: Always look for ways to simplify a problem by the use of symmetry. This is especially true for situations involving circles or spheres. © 2019 Mc. Graw-Hill Education.

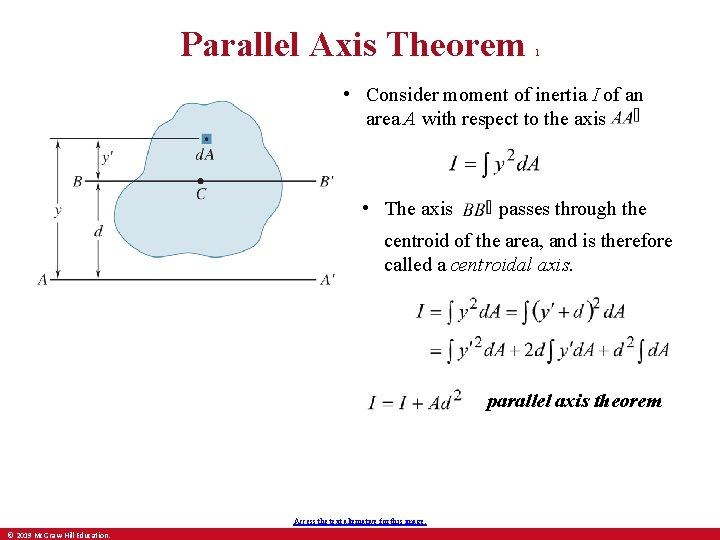
Parallel Axis Theorem 1 • Consider moment of inertia I of an area A with respect to the axis • The axis passes through the centroid of the area, and is therefore called a centroidal axis. parallel axis theorem Access the text alternative for this image. © 2019 Mc. Graw-Hill Education.

Parallel Axis Theorem 2 • Moment of inertia IT of a circular area with respect to a tangent to the circle, • Moment of inertia of a triangle with respect to a centroidal axis, Access the text alternative for these images. © 2019 Mc. Graw-Hill Education.

Moments of Inertia of Composite Areas • The moment of inertia of a composite area A about a given axis is obtained by adding the moments of inertia of the component areas A 1, A 2, A 3, . . . , with respect to the same axis. © 2019 Mc. Graw-Hill Education. 1

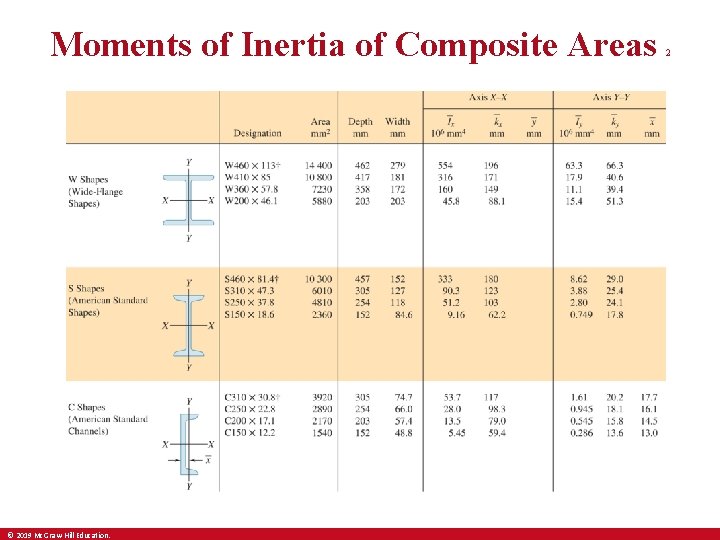
Moments of Inertia of Composite Areas © 2019 Mc. Graw-Hill Education. 2

Sample Problem 9. 4 1 Strategy: • Determine location of the centroid of composite section with respect to a coordinate system having its origin at the centroid of the beam section. The strength of a W 14× 38 rolled steel beam is increased by attaching a plate to its upper flange. Determine the moment of inertia and radius of gyration with respect to an axis that is parallel to the plate and passes through the centroid of the section. © 2019 Mc. Graw-Hill Education. • Apply the parallel axis theorem to determine moments of inertia of beam section and plate with respect to the composite section’s centroidal axis. • Calculate the radius of gyration from the moment of inertia of the composite section.

Sample Problem 9. 4 2 Modeling and Analysis: • Determine location of the centroid of composite section with respect to a coordinate system with origin at the centroid of the beam section. Section Plate 6. 75 7. 425 50. 12 Beam Section 11. 20 0 0 blank © 2019 Mc. Graw-Hill Education. blank

Sample Problem 9. 4 3 • Apply the parallel axis theorem to determine moments of inertia of the beam section and the plate with respect to the composite section’s centroidal axis. • Calculate the radius of gyration from the moment of inertia of the composite section. © 2019 Mc. Graw-Hill Education.

Sample Problem 9. 4 4 Reflect and Think: This is a common type of calculation for many different situations. It is often helpful to list data in a table to keep track of the numbers and identify which data you need. © 2019 Mc. Graw-Hill Education.

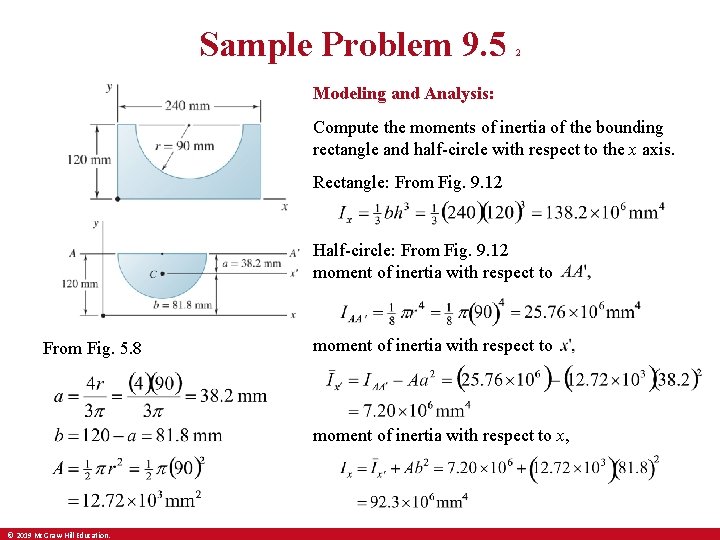
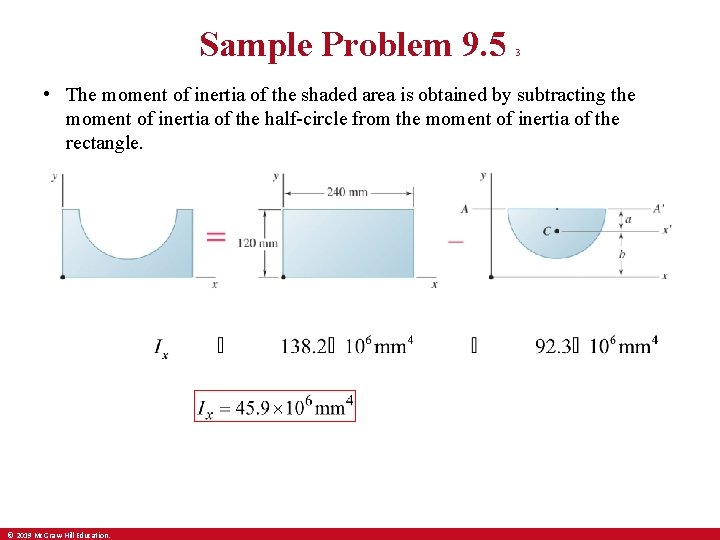
Sample Problem 9. 5 1 Strategy: • Compute the moments of inertia of the rectangle and half-circle with respect to the x axis. Determine the moment of inertia of the shaded area with respect to the x axis. List the steps of your solution. Be specific in exactly what expressions you would use from the table of moments of inertia of common shapes, and how you would apply the parallel axis theorem. Compare your solution with a neighbor. begin underline end underline © 2019 Mc. Graw-Hill Education. • The moment of inertia of the shaded area is obtained by subtracting the moment of inertia of the half-circle from the moment of inertia of the rectangle.

Sample Problem 9. 5 2 Modeling and Analysis: Compute the moments of inertia of the bounding rectangle and half-circle with respect to the x axis. Rectangle: From Fig. 9. 12 Half-circle: From Fig. 9. 12 moment of inertia with respect to From Fig. 5. 8 moment of inertia with respect to x, © 2019 Mc. Graw-Hill Education.

Sample Problem 9. 5 3 • The moment of inertia of the shaded area is obtained by subtracting the moment of inertia of the half-circle from the moment of inertia of the rectangle. © 2019 Mc. Graw-Hill Education.

Sample Problem 9. 5 4 Two important things to note: 1. The moments of inertia had to reference the same axis. 2. The parallel axis theorem had to be applied twice to the semicircle. Why? Reflect and Think: Figures 5. 8 and 9. 12 are useful references for locating centroids and moments of inertia of common areas; don’t forget to use them. © 2019 Mc. Graw-Hill Education.

Product of Inertia • Product of Inertia: • When the x axis, the y axis, or both are an axis of symmetry, the product of inertia is zero. • Parallel axis theorem for products of inertia: © 2019 Mc. Graw-Hill Education.

Principal Axes and Principal Moments of Inertia 1 • The change of axes yields Given we wish to determine moments and product of inertia with respect to new axes x′ and y′. • The equations for are the parametric equations for a circle, Note: • The equations for lead to the same circle. © 2019 Mc. Graw-Hill Education.

Principal Axes and Principal Moments of Inertia 2 • At the points A and B, is a maximum and minimum, respectively. • The equation for m defines two angles, 90 o apart, that correspond to the principal axes of the area about O. • Imax and Imin are the principal moments of inertia of the area about O. © 2019 Mc. Graw-Hill Education.

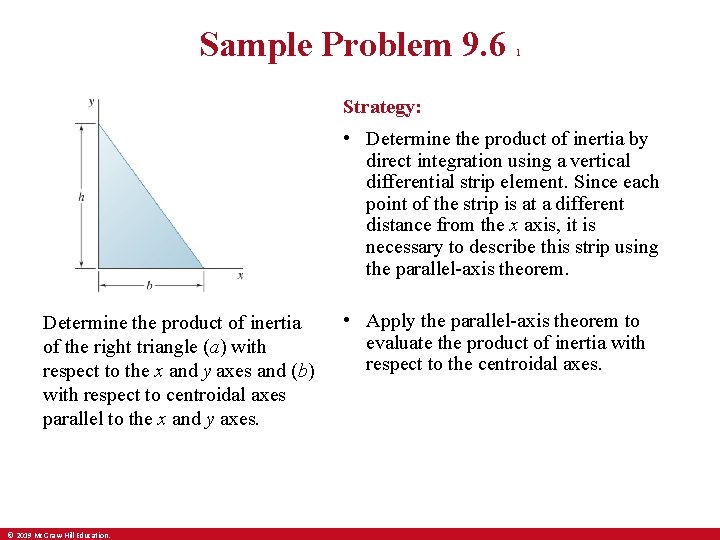
Sample Problem 9. 6 1 Strategy: • Determine the product of inertia by direct integration using a vertical differential strip element. Since each point of the strip is at a different distance from the x axis, it is necessary to describe this strip using the parallel-axis theorem. Determine the product of inertia of the right triangle (a) with respect to the x and y axes and (b) with respect to centroidal axes parallel to the x and y axes. © 2019 Mc. Graw-Hill Education. • Apply the parallel-axis theorem to evaluate the product of inertia with respect to the centroidal axes.

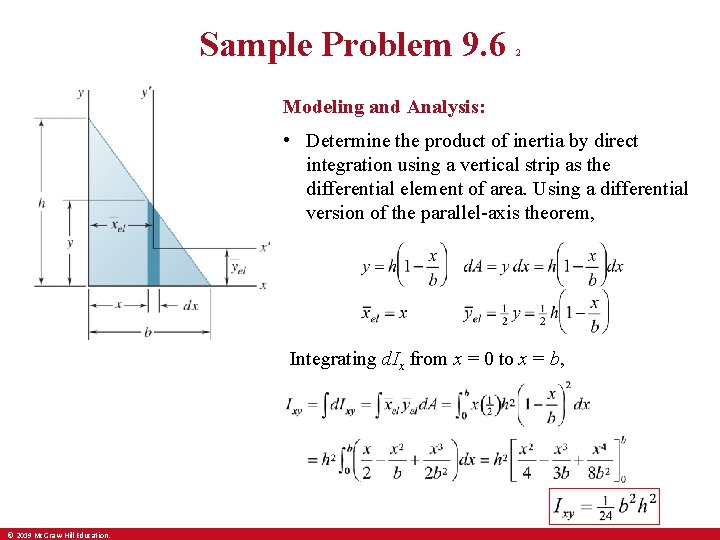
Sample Problem 9. 6 2 Modeling and Analysis: • Determine the product of inertia by direct integration using a vertical strip as the differential element of area. Using a differential version of the parallel-axis theorem, Integrating d. Ix from x = 0 to x = b, © 2019 Mc. Graw-Hill Education.

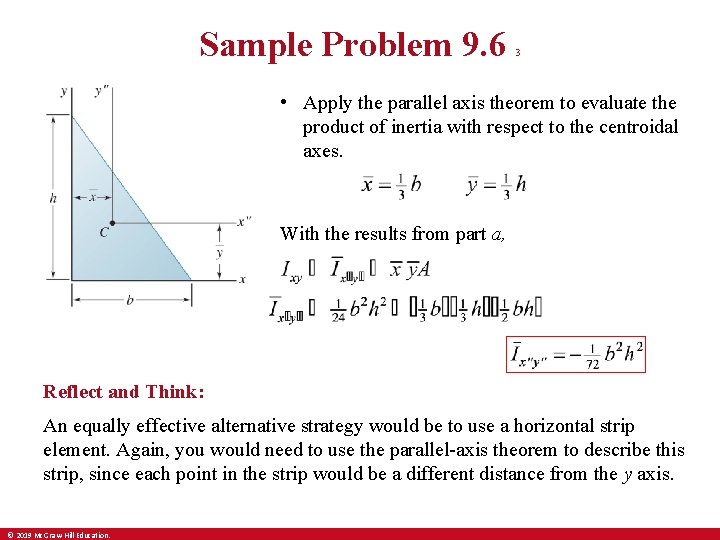
Sample Problem 9. 6 3 • Apply the parallel axis theorem to evaluate the product of inertia with respect to the centroidal axes. With the results from part a, Reflect and Think: An equally effective alternative strategy would be to use a horizontal strip element. Again, you would need to use the parallel-axis theorem to describe this strip, since each point in the strip would be a different distance from the y axis. © 2019 Mc. Graw-Hill Education.

Sample Problem 9. 7 1 Strategy: • Compute the product of inertia with respect to the xy axes by dividing the section into three rectangles and applying the parallel axis theorem to each. For the section shown, the moments of inertia with respect to the x and y axes are Determine (a) the orientation of the principal axes of the section about O, and (b) the values of the principal moments of inertia about O. © 2019 Mc. Graw-Hill Education. • Determine the orientation of the principal axes using Eq. (9. 25), and find the principal moments of inertia using Eq. (9. 27).

Sample Problem 9. 7 2 Modeling and Analysis: • Compute the product of inertia with respect to the xy axes by dividing the section into three rectangles. Apply the parallel axis theorem to each rectangle, Note that the product of inertia with respect to centroidal axes parallel to the xy axes is zero for each rectangle. Rectangle I 1. 5 − 1. 25 +1. 75 − 3. 28 II 1. 5 0 0 0 III 1. 5 +1. 25 − 1. 75 − 3. 28 Blank © 2019 Mc. Graw-Hill Education. Area, in 2

Sample Problem 9. 7 3 • Find the orientation of the principal axes using Eq. (9. 25) and the principal moments of inertia using Eq. (9. 27). Reflect and Think: Note that the elements of the area of the section are more closely distributed about the b axis than about the a axis. Therefore, you can conclude that Ia = Imax = 15. 45 in 4 and Ib = Imin = 1. 897 in 4. You can verify this conclusion by substituting θ = 37. 7° into Eqs. (9. 18) and (9. 19). © 2019 Mc. Graw-Hill Education.

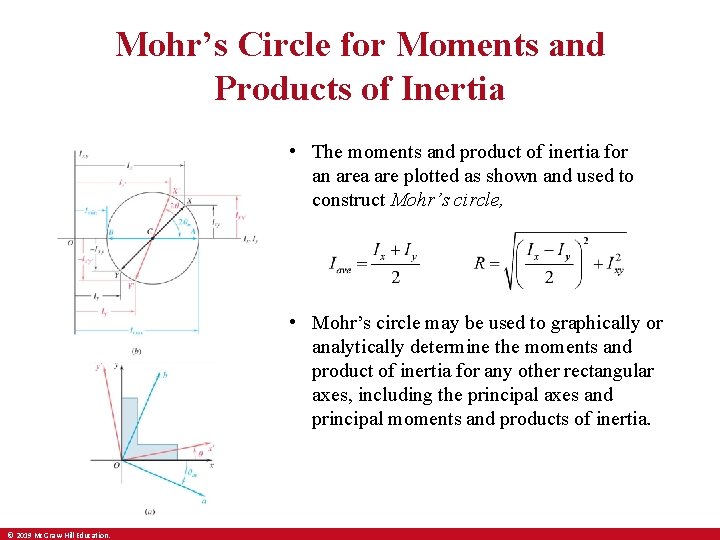
Mohr’s Circle for Moments and Products of Inertia • The moments and product of inertia for an area are plotted as shown and used to construct Mohr’s circle, • Mohr’s circle may be used to graphically or analytically determine the moments and product of inertia for any other rectangular axes, including the principal axes and principal moments and products of inertia. © 2019 Mc. Graw-Hill Education.

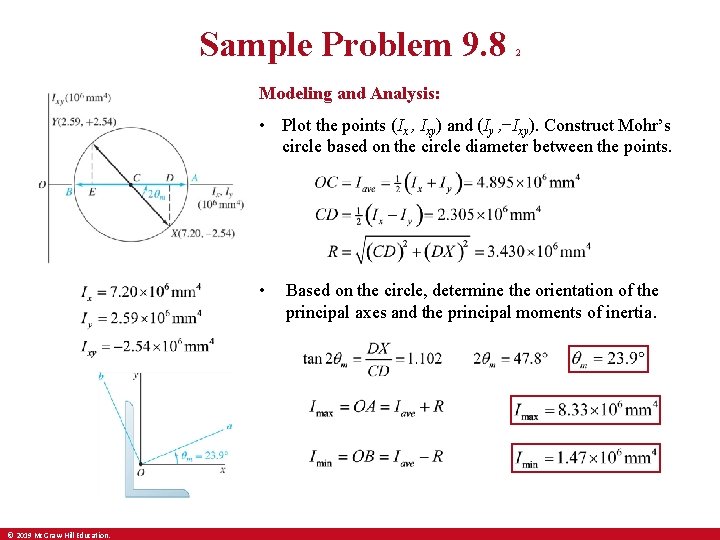
Sample Problem 9. 8 1 Strategy: • Plot the points (Ix , Ixy) and (Iy, −Ixy). Construct Mohr’s circle based on the circle diameter between the points. The moments and product of inertia with respect to the x and y axes are Using Mohr’s circle, determine (a) the principal axes about O, (b) the values of the principal moments of inertia about O, and (c) the values of the moments and product of inertia about the xʹ and yʹ axes that form an angle of 60°with the x and y axes. © 2019 Mc. Graw-Hill Education. • Based on the circle, determine the orientation of the principal axes and the principal moments of inertia. • Based on the circle, evaluate the moments and product of inertia with respect to the xʹ and yʹ axes.

Sample Problem 9. 8 2 Modeling and Analysis: • Plot the points (Ix , Ixy) and (Iy , −Ixy). Construct Mohr’s circle based on the circle diameter between the points. • © 2019 Mc. Graw-Hill Education. Based on the circle, determine the orientation of the principal axes and the principal moments of inertia.

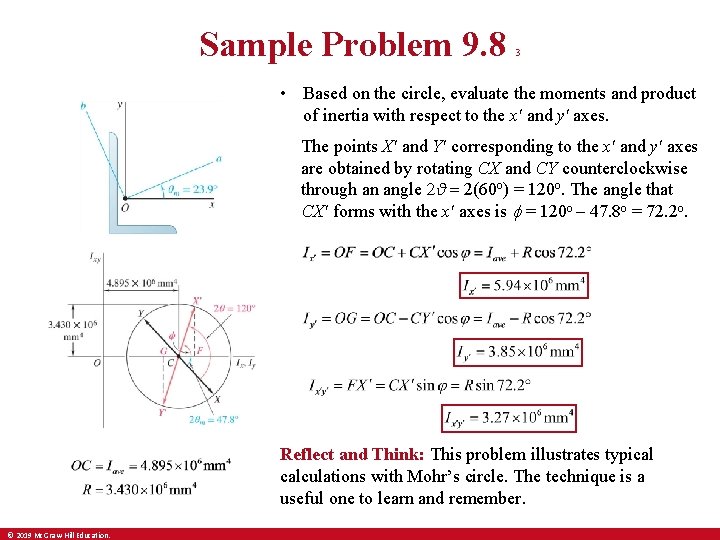
Sample Problem 9. 8 3 • Based on the circle, evaluate the moments and product of inertia with respect to the xʹ and yʹ axes. The points X′ and Y′ corresponding to the x′ and y′ axes are obtained by rotating CX and CY counterclockwise through an angle 2θ = 2(60 o) = 120 o. The angle that CX′ forms with the x′ axes is f = 120 o – 47. 8 o = 72. 2 o. Reflect and Think: This problem illustrates typical calculations with Mohr’s circle. The technique is a useful one to learn and remember. © 2019 Mc. Graw-Hill Education.

Moment of Inertia of a Simple Mass • Angular acceleration about the axis of the small mass Dm due to the application of a couple is proportional to = moment of inertia of the mass Dm with respect to the axis • For a body of mass m the resistance to rotation about the axis • The radius of gyration for a concentrated mass with equivalent mass moment of inertia is © 2019 Mc. Graw-Hill Education.

Moment of Inertia of a Mass • Moment of inertia with respect to the y coordinate axis is • Similarly, for the moment of inertia with respect to the x and z axes, • In SI units In U. S. customary units, © 2019 Mc. Graw-Hill Education.

Parallel Axis Theorem • For the rectangular axes with origin at O and parallel centroidal axes, • Generalizing for any axis and a parallel centroidal axis, © 2019 Mc. Graw-Hill Education.

Moments of Inertia of Thin Plates 1 • For a thin plate of uniform thickness t and homogeneous material of density r, the mass moment of inertia with respect to axis contained in the plate is • Similarly, for perpendicular axis which is also contained in the plate, • For the axis © 2019 Mc. Graw-Hill Education. which is perpendicular to the plate,

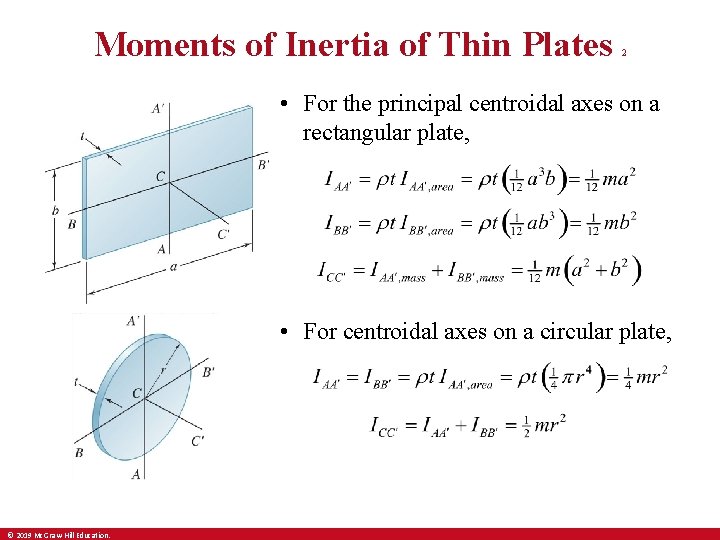
Moments of Inertia of Thin Plates 2 • For the principal centroidal axes on a rectangular plate, • For centroidal axes on a circular plate, © 2019 Mc. Graw-Hill Education.

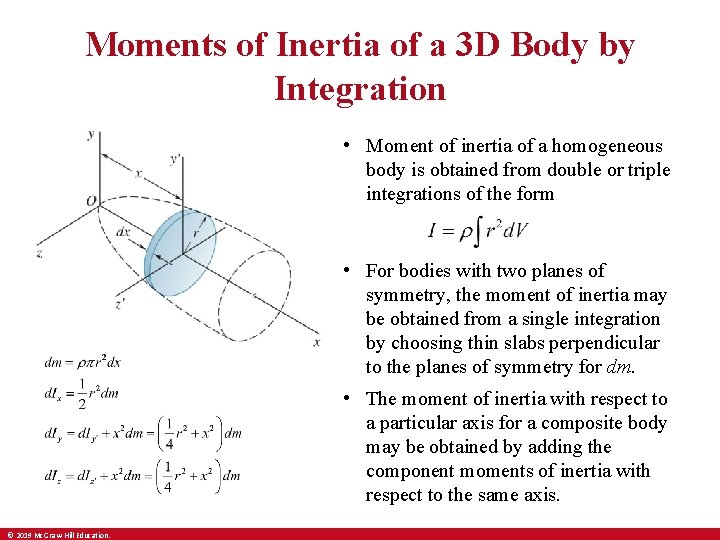
Moments of Inertia of a 3 D Body by Integration • Moment of inertia of a homogeneous body is obtained from double or triple integrations of the form • For bodies with two planes of symmetry, the moment of inertia may be obtained from a single integration by choosing thin slabs perpendicular to the planes of symmetry for dm. • The moment of inertia with respect to a particular axis for a composite body may be obtained by adding the component moments of inertia with respect to the same axis. © 2019 Mc. Graw-Hill Education.

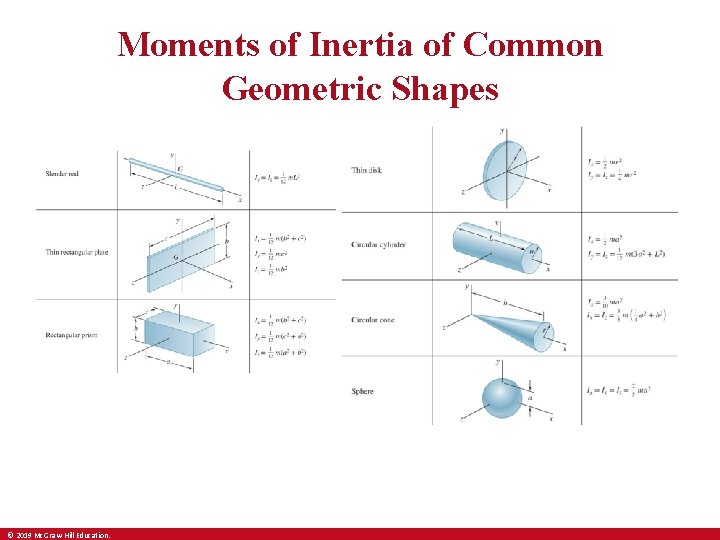
Moments of Inertia of Common Geometric Shapes © 2019 Mc. Graw-Hill Education.

Sample Problem 9. 12 1 Strategy: • With the forging divided into a prism and two cylinders, compute the mass and moments of inertia of each component with respect to the xyz axes using the parallel axis theorem. • Add the moments of inertia from the components to determine the total moments of inertia for the forging. Determine the moments of inertia of the steel forging with respect to the xyz coordinate axes, knowing that the specific weight of steel is 490 lb/ft 3. Access the text alternative for this image. © 2019 Mc. Graw-Hill Education.

Sample Problem 9. 12 Modeling and Analysis: • Compute the moments of inertia of each component with respect to the xyz axes. cylinders Access the text alternative for this image. © 2019 Mc. Graw-Hill Education. 2

Sample Problem 9. 12 3 prism (a = 2 in. , b = 6 in. , c = 2 in. ): • Add the component moments of inertia to determine the total moments of inertia. Access the text alternative for this image. © 2019 Mc. Graw-Hill Education.

Sample Problem 9. 12 4 Reflect and Think: The results indicate this forging has more resistance to rotation about the z axis (largest moment of inertia) than about the x or y axes. This makes intuitive sense, because more of the mass is farther from the z axis than from the x or y axes. © 2019 Mc. Graw-Hill Education.

Mass Products of Inertia • IOL = moment of inertia with respect to axis OL • Expressing in terms of the vector components and expanding yields • The definition of the mass products of inertia of a mass is an extension of the definition of product of inertia of an area © 2019 Mc. Graw-Hill Education.

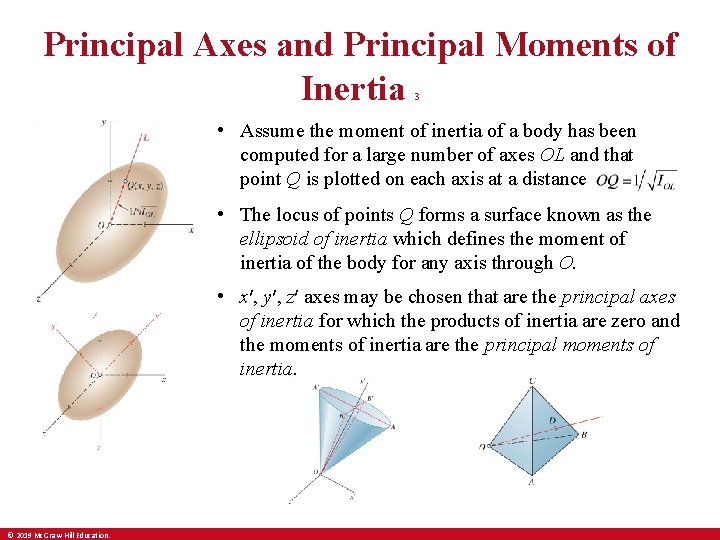
Principal Axes and Principal Moments of Inertia 3 • Assume the moment of inertia of a body has been computed for a large number of axes OL and that point Q is plotted on each axis at a distance • The locus of points Q forms a surface known as the ellipsoid of inertia which defines the moment of inertia of the body for any axis through O. • x′, y′, z′ axes may be chosen that are the principal axes of inertia for which the products of inertia are zero and the moments of inertia are the principal moments of inertia. © 2019 Mc. Graw-Hill Education.

End of Chapter 9 © 2019 Mc. Graw-Hill Education.