Unit III Inequalities What is an inequality Inequalities

Unit III Inequalities

What is an inequality? Inequalities work like equations, but they tell you whether one expression is bigger or smaller than the expression on the other side. An inequality is like an equation, but instead of an equal sign (=) it has one of these signs: < “is less than” > “is greater than” £ “is less than or equal to” ³ “is greater than or equal to” An inequality is a mathematical sentence that states that two expressions are not equal.

"Solving'' an inequality means finding all of its solutions. A "solution'' of an inequality is a number which when substituted for the variable makes the inequality a true statement. Inequality symbols < • less than • fewer than > £ • greater than • less than or equal to • more than • no more • exceeds than • at most ³ • greater than or equal to • no less than • at least

Graphing Inequalities x<c When x is less than a constant, you darken in the part of the number line that is to the left of the constant. Also, because there is no equal line, we are not including where x is equal to the constant. That means we are not including the endpoint. One way to notate that is to use an open hole at that point. x>c When x is greater than a constant, you darken in the part of the number line that is to the right of the constant. Also, because there is no equal line, we are not including where x is equal to the constant. That means we are not including the endpoint. One way to notate that is to use an open hole at that point.

x<c When x is less than or equal to a constant, you darken in the part of the number line that is to the left of the constant. Also, because there is an equal line, we are including where x is equal to the constant. That means we are including the endpoint. One way to notate that is to use an closed hole at that point. x>c When x is greater than or equal to a constant, you darken in the part of the number line that is to the right of the constant. Also, because there is an equal line, we are including where x is equal to the constant. That means we are including the endpoint. One way to notate that is to use a closed hole at that point.

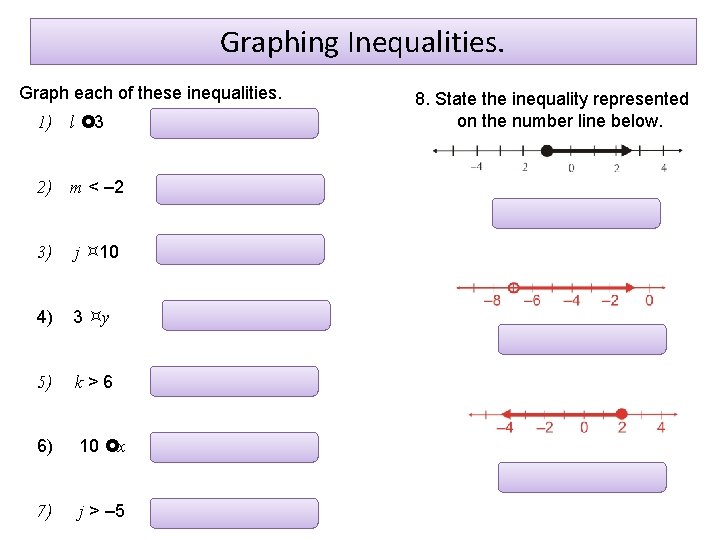
Graphing Inequalities. Graph each of these inequalities. 1) l £ 3 2) m < – 2 8. State the inequality represented on the number line below. x ³– 1 3) j ³ 10 4) 3 ³y k > – 7 5) k>6 6) 10 £x k £ 2 7) j > – 5

Applications Anthony is shopping for a birthday gift for his cousin Robert. He has $25 dollars in his wallet. Write an inequality that shows how many dollars he can spend on the gift. a £ 25 Teresa is only allowed to swim outside if the temperature outside is at least 85 °F. Write an inequality that shows the temperature in degrees Fahrenheit at which Teresa is allowed to swim. t ³ 85 In order to achieve an ‘A’ in math, Ivy needs to score more than 95% on her next test. Write an inequality that shows the test score Ivy needs to achieve in order to earn her ‘A’ in math. i > 95

Addition/Subtraction Property for Inequalities If a < b, then a + c < b + c If a < b, then a - c < b – c In other words, adding or subtracting the same expression to both sides of an inequality does not change the inequality. Ex. A Solve and graph the solution of x – 2 > 5 on a number line. Solve: x– 2>5 +2 +2 x>7 Graph: – 7 Ex. B Solve and then graph the solution of 3 x £ 6 + 2 x on a number line. Solve: 3 x £ 6 + 2 x -2 x Using addition property of inequalities -2 x Subtraction property of inequalities x £ 6 Graph: 0 7 – 1 0 1 2 3 4 5 6

Practice Solve and graph each inequality. 1) x + 2 < 8 x<6 2) j + 2 ³– 3 3) 4 x – 3 < j ³– 5 3 x 4) 2 t + 1 £t – 10 x<3 t £– 11 5) 6(x – 1) ³ 5(x + 2) x ³ 16

Applications Stephen needs to buy a new uniform for soccer. He already has $25, but the uniform costs $55. He participates in car washes to help pay for the uniform. Write an inequality to represent the amount of money, x, that Stephen needs to earn from the car washes in order to be able to afford the new uniform. Use this inequality to find the minimum amount of money he needs to earn. x ³ 30; minimum = $30 An art gallery sells Peter’s paintings for $x, and keeps $100 commission. This means Peter is paid $(x – 100) for each painting. If Peter wants to make at least $750 for a particular painting, write an inequality to represent the amount, x, that the gallery needs to sell that painting for. Use this inequality to find the minimum price of the painting. x ³ 850 minimum = $850

Multiplication/Division Properties for Inequalities when multiplying/dividing by a positive value If a < b AND c is positive, then ac < bc If a < b AND c is positive, then a/c < b/c In other words, multiplying or dividing the same POSITIVE number to both sides of an inequality does not change the inequality. Solve Solution Given Inequality Multiplication Property x > 10 ___ 3 3 x<4 Division Property

Multiplication/Division Properties for Inequalities with NEGATIVE Numbers Given real numbers a, b, and c, if a > b and c < 0 then ac < bc. a < b Given real numbers a, b, and c, if a > b and c < 0 then c c In other words, multiplying or dividing the same NEGATIVE number to both sides of an inequality REVERSES the direction of the inequality, otherwise the inequality statement will be false. Solve: Solution: x < – 4 Remember — the sign needs to change.

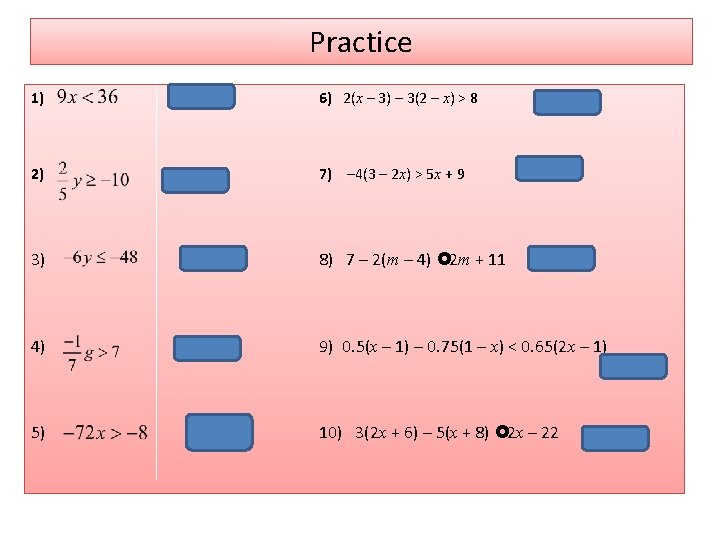
Practice 1) 6) 2(x – 3) – 3(2 – x) > 8 2) 7) – 4(3 – 2 x) > 5 x + 9 3) 8) 7 – 2(m – 4) £ 2 m + 11 4) 9) 0. 5(x – 1) – 0. 75(1 – x) < 0. 65(2 x – 1) x > – 12 5) 10) 3(2 x + 6) – 5(x + 8) £ 2 x – 22 x>4 x>7 m ³ 1 x ³ 0

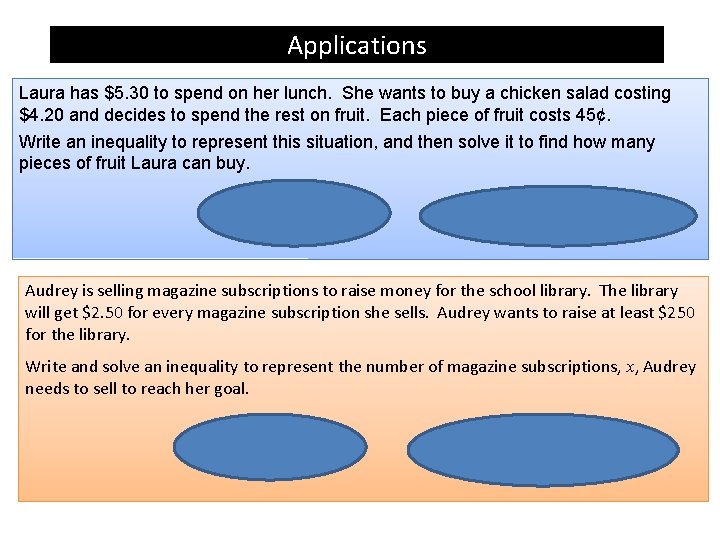
Applications Laura has $5. 30 to spend on her lunch. She wants to buy a chicken salad costing $4. 20 and decides to spend the rest on fruit. Each piece of fruit costs 45¢. Write an inequality to represent this situation, and then solve it to find how many pieces of fruit Laura can buy. 4. 20 + 0. 45 x £ 5. 30 x £ 2. 44 Laura can buy 2 pieces of fruit Audrey is selling magazine subscriptions to raise money for the school library. The library will get $2. 50 for every magazine subscription she sells. Audrey wants to raise at least $250 for the library. Write and solve an inequality to represent the number of magazine subscriptions, x, Audrey needs to sell to reach her goal. 2. 50 x ³ 250 x ³ 100 Audrey must sell at least 100 magazine subscriptions

Multistep Inequalities To simplify and therefore solve an inequality in one variable such as x, you need to isolate the terms in x on one side and isolate the numbers on the other. Solving Inequalities 1. Multiply out any parentheses 2. Simplify each side of the inequality. 3. Remove number terms from one side 4. Remove x-terms from the other side. 5. Multiply or divide to get an x-coefficient of 1

Practice 1) 6 x – 2 £ 4(x + 5) x £ 11 2) 5 x + 1 > 3(x + 3) x>4 3) 4(x + 1) > 2 x 6 x < 0. 5 8(x – 1) ³ 4 x – 4 x ³ 1 4) 5) 7(a – 4) £ 4 a 2 a > -28

Compound Inequalities A compound inequality is two inequalities together — for example, 2 x + 1 < 5 and 2 x + 1 > – 1. The word “and” means the compound inequality below is a “conjunction. ” 2 x + 1 < 5 and 2 x + 1 > – 1 Solve and graph the inequality – 1 < 2 x + 1 < 5. The goal is to get x by itself. – 1 < 2 x + 1 < 5 -1 You can rewrite a conjunction as a single mathematical statement, usually involving two inequality signs, like this: – 1 < 2 x + 1 < 5 * The solution to a conjunction must satisfy both inequalities — both inequalities must be true. -1 -1 – 2 < 2 x < 4 – 1 < x < 2 Subtract 1 Divide by 2 to get x in the middle the solution is any number greater than – 1 but less than 2

Disjunction Problems Include the Word “Or” Here’s an example of a disjunction: 3 x – 4 < – 4 or 3 x – 4 > 4 The solution to a disjunction is all the numbers that satisfy either one inequality or the other. Solve and graph the solution set of 3 x – 4 < – 4 or 3 x – 4 > 4. 3 x – 4 + 4 < – 4 + 4 or or 3 x – 4 + 4 > 4 + 4 3 x < 0 or 3 x > 8 x<0 or 8 x> 3 Add 4 Divide by 3

Compound Inequalities Practice 1) – 11 < – 4 g + 5 < – 3 2) – 16 < – 4 g < – 8 2<g<4 8 c – 4 > 92 or 8 c – 4 < – 12 8 c > 96 or 8 c < – 8 c > 12 or c < – 1 3) 2 y + 2 < 4 y – 4 or 4 y – 4 > 5 y + 2 4) – 9 g – 7 £ 2 or – 9 g – 7 > 20 5) 3 £ 3(2 x – 5) £ 9 6) – 11 < c– 9 7 y > 3 or y < – 6 – 9 g £ 9 or – 9 g > 27 g ³– 1 or g < – 3 3 £x £ 4 <5 – 77 < c – 9 < 35 – 68 < c < 44

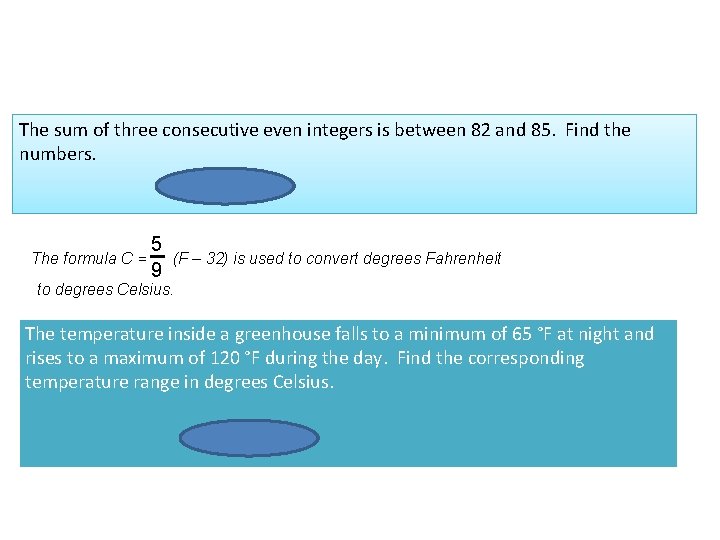
The sum of three consecutive even integers is between 82 and 85. Find the numbers. 26, 28, and 30 The formula C = 5 9 (F – 32) is used to convert degrees Fahrenheit to degrees Celsius. The temperature inside a greenhouse falls to a minimum of 65 °F at night and rises to a maximum of 120 °F during the day. Find the corresponding temperature range in degrees Celsius. 18 °C – 49 °C