U D 8 4 ESO E AP MEDIDA

U. D. 8 * 4º ESO E. AP. MEDIDA DE LONGITUDES @ Angel Prieto Benito Matemáticas 4º ESO E. AP. 1

U. D. 8. 3 * 4º ESO E. AP. PITÁGORAS EN EL ESPACIO @ Angel Prieto Benito Matemáticas 4º ESO E. AP. 2

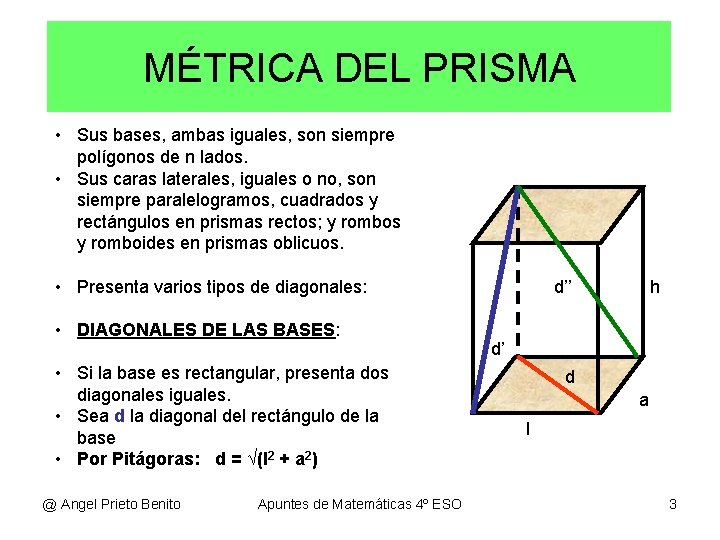
MÉTRICA DEL PRISMA • Sus bases, ambas iguales, son siempre polígonos de n lados. • Sus caras laterales, iguales o no, son siempre paralelogramos, cuadrados y rectángulos en prismas rectos; y rombos y romboides en prismas oblicuos. • Presenta varios tipos de diagonales: • DIAGONALES DE LAS BASES: • Si la base es rectangular, presenta dos diagonales iguales. • Sea d la diagonal del rectángulo de la base • Por Pitágoras: d = √(l 2 + a 2) @ Angel Prieto Benito Apuntes de Matemáticas 4º ESO d’’ h d’ d a l 3

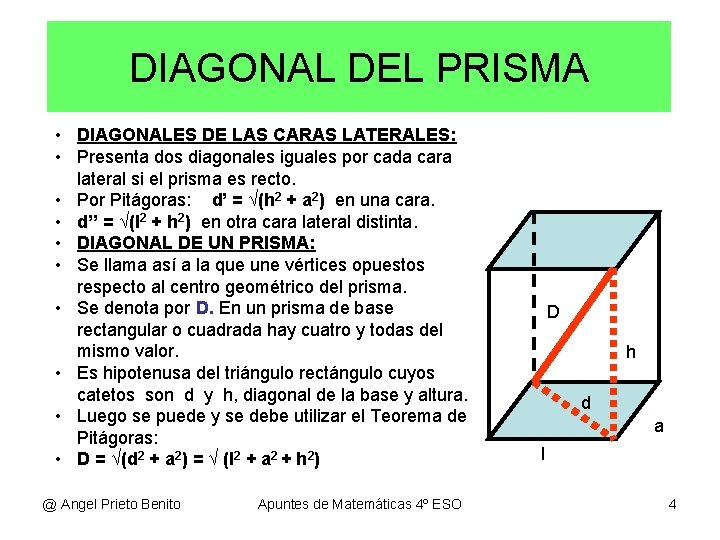
DIAGONAL DEL PRISMA • DIAGONALES DE LAS CARAS LATERALES: • Presenta dos diagonales iguales por cada cara lateral si el prisma es recto. • Por Pitágoras: d’ = √(h 2 + a 2) en una cara. • d’’ = √(l 2 + h 2) en otra cara lateral distinta. • DIAGONAL DE UN PRISMA: • Se llama así a la que une vértices opuestos respecto al centro geométrico del prisma. • Se denota por D. En un prisma de base rectangular o cuadrada hay cuatro y todas del mismo valor. • Es hipotenusa del triángulo rectángulo cuyos catetos son d y h, diagonal de la base y altura. • Luego se puede y se debe utilizar el Teorema de Pitágoras: • D = √(d 2 + a 2) = √ (l 2 + a 2 + h 2) @ Angel Prieto Benito Apuntes de Matemáticas 4º ESO D h d a l 4

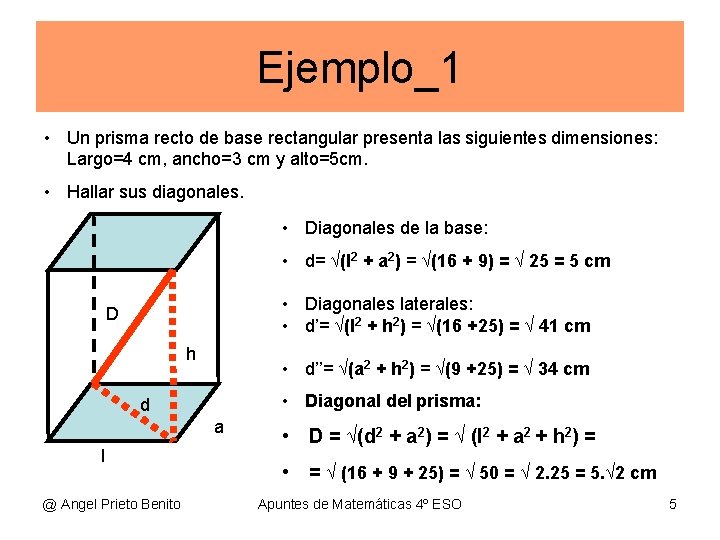
Ejemplo_1 • Un prisma recto de base rectangular presenta las siguientes dimensiones: Largo=4 cm, ancho=3 cm y alto=5 cm. • Hallar sus diagonales. • Diagonales de la base: • d= √(l 2 + a 2) = √(16 + 9) = √ 25 = 5 cm • Diagonales laterales: • d’= √(l 2 + h 2) = √(16 +25) = √ 41 cm D h • d’’= √(a 2 + h 2) = √(9 +25) = √ 34 cm • Diagonal del prisma: d a l @ Angel Prieto Benito • D = √(d 2 + a 2) = √ (l 2 + a 2 + h 2) = • = √ (16 + 9 + 25) = √ 50 = √ 2. 25 = 5. √ 2 cm Apuntes de Matemáticas 4º ESO 5

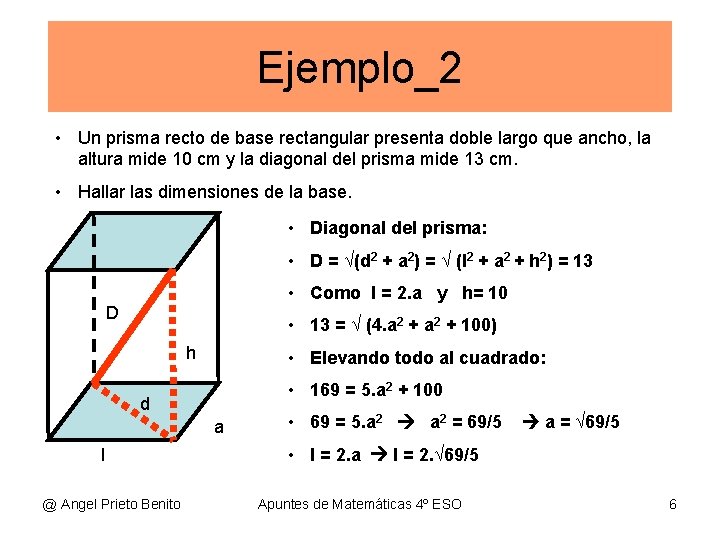
Ejemplo_2 • Un prisma recto de base rectangular presenta doble largo que ancho, la altura mide 10 cm y la diagonal del prisma mide 13 cm. • Hallar las dimensiones de la base. • Diagonal del prisma: • D = √(d 2 + a 2) = √ (l 2 + a 2 + h 2) = 13 • Como l = 2. a y h= 10 D • 13 = √ (4. a 2 + 100) h • Elevando todo al cuadrado: • 169 = 5. a 2 + 100 d a l @ Angel Prieto Benito • 69 = 5. a 2 = 69/5 a = √ 69/5 • l = 2. a l = 2. √ 69/5 Apuntes de Matemáticas 4º ESO 6

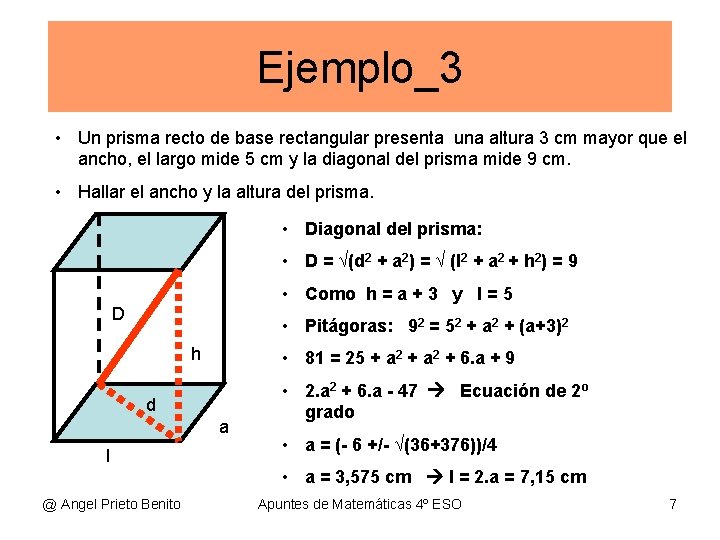
Ejemplo_3 • Un prisma recto de base rectangular presenta una altura 3 cm mayor que el ancho, el largo mide 5 cm y la diagonal del prisma mide 9 cm. • Hallar el ancho y la altura del prisma. • Diagonal del prisma: • D = √(d 2 + a 2) = √ (l 2 + a 2 + h 2) = 9 • Como h = a + 3 y l = 5 D • Pitágoras: 92 = 52 + a 2 + (a+3)2 h • 81 = 25 + a 2 + 6. a + 9 d a l • 2. a 2 + 6. a - 47 Ecuación de 2º grado • a = (- 6 +/- √(36+376))/4 • a = 3, 575 cm l = 2. a = 7, 15 cm @ Angel Prieto Benito Apuntes de Matemáticas 4º ESO 7

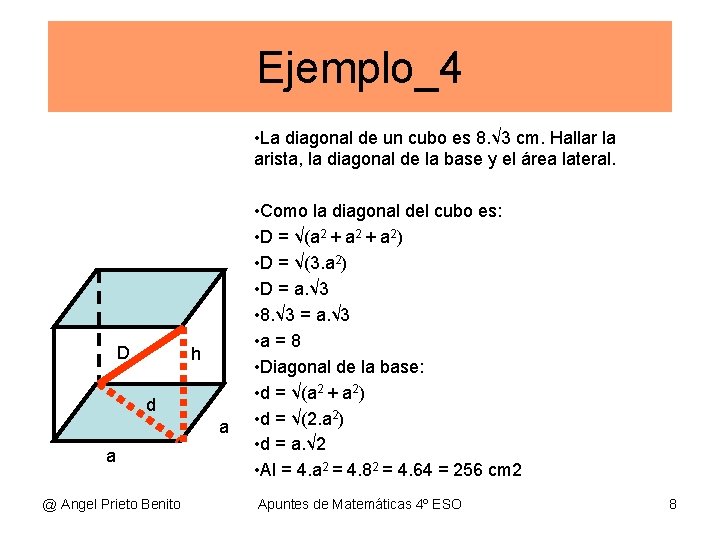
Ejemplo_4 • La diagonal de un cubo es 8. √ 3 cm. Hallar la arista, la diagonal de la base y el área lateral. D h d a a @ Angel Prieto Benito • Como la diagonal del cubo es: • D = √(a 2 + a 2) • D = √(3. a 2) • D = a. √ 3 • 8. √ 3 = a. √ 3 • a = 8 • Diagonal de la base: • d = √(a 2 + a 2) • d = √(2. a 2) • d = a. √ 2 • Al = 4. a 2 = 4. 82 = 4. 64 = 256 cm 2 Apuntes de Matemáticas 4º ESO 8

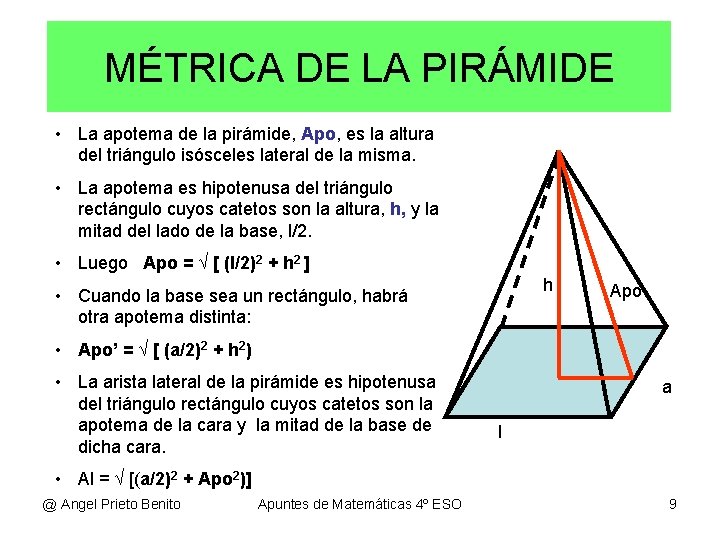
MÉTRICA DE LA PIRÁMIDE • La apotema de la pirámide, Apo, es la altura del triángulo isósceles lateral de la misma. • La apotema es hipotenusa del triángulo rectángulo cuyos catetos son la altura, h, y la mitad del lado de la base, l/2. • Luego Apo = √ [ (l/2)2 + h 2 ] h • Cuando la base sea un rectángulo, habrá otra apotema distinta: Apo • Apo’ = √ [ (a/2)2 + h 2) • La arista lateral de la pirámide es hipotenusa del triángulo rectángulo cuyos catetos son la apotema de la cara y la mitad de la base de dicha cara. a l • Al = √ [(a/2)2 + Apo 2)] @ Angel Prieto Benito Apuntes de Matemáticas 4º ESO 9

Ejemplo_1 • Una pirámide recta de base cuadrangular presenta una altura de 4 cm y un lado de la base de 6 cm. • Hallar el perímetro de la base, la apotema y la arista lateral. • P = 4. l = 4. 6 = 24 cm • Por Pitágoras: • apo = √ [ (l/2)2 + h 2) • Apo = √ [ (6/2)2 + 42 ] = √ 25 = 5 cm apo • Arista lateral: • Por Pitágoras: al • al = √ [ (l/2)2 + apo 2) = √ 9 + 25 = l/2 • = √ 34 cm @ Angel Prieto Benito Apuntes de Matemáticas 4º ESO l l 10

Ejemplo_2 • La apotema señalada en la figura de la pirámide 7 cm, y la altura es 1 cm mayor que el ancho de la base. Hallar el ancho y la altura. • Por Pitágoras: • Apo = √ [ (a/2)2 + h 2) 7 = √ [ (a/2)2 + (a+1)2 ] • Elevando todo al cuadrado: • 49 = (a 2 / 4) + a 2 + 2. a + 1 • 196 = 5. a 2 + 8. a + 4 h • 5. a 2 + 8. a – 192 = 0 Apo • Resolviendo … a = 5, 45 cm • El otro valor de a, negativo, no vale. a • Luego h = a+1 = 6, 45 cm @ Angel Prieto Benito Apuntes de Matemáticas 4º ESO l 11

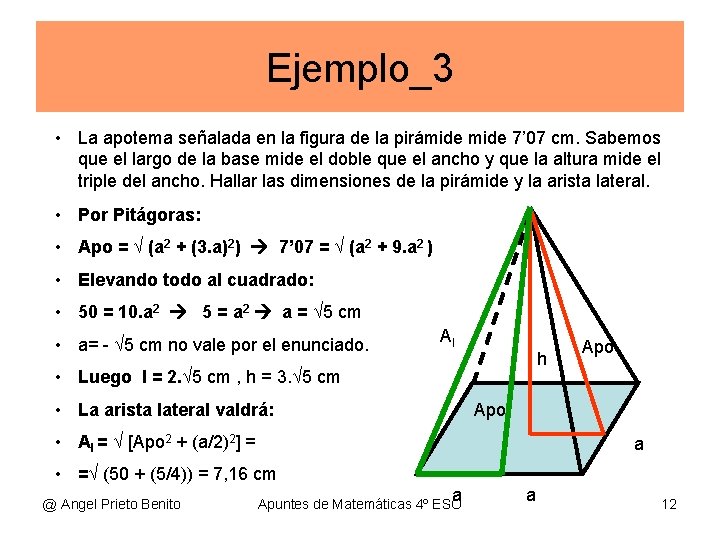
Ejemplo_3 • La apotema señalada en la figura de la pirámide 7’ 07 cm. Sabemos que el largo de la base mide el doble que el ancho y que la altura mide el triple del ancho. Hallar las dimensiones de la pirámide y la arista lateral. • Por Pitágoras: • Apo = √ (a 2 + (3. a)2) 7’ 07 = √ (a 2 + 9. a 2 ) • Elevando todo al cuadrado: • 50 = 10. a 2 5 = a 2 a = √ 5 cm • a= - √ 5 cm no vale por el enunciado. Al h • Luego l = 2. √ 5 cm , h = 3. √ 5 cm • La arista lateral valdrá: Apo • Al = √ [Apo 2 + (a/2)2] = a • =√ (50 + (5/4)) = 7, 16 cm @ Angel Prieto Benito a Apuntes de Matemáticas 4º ESO a 12

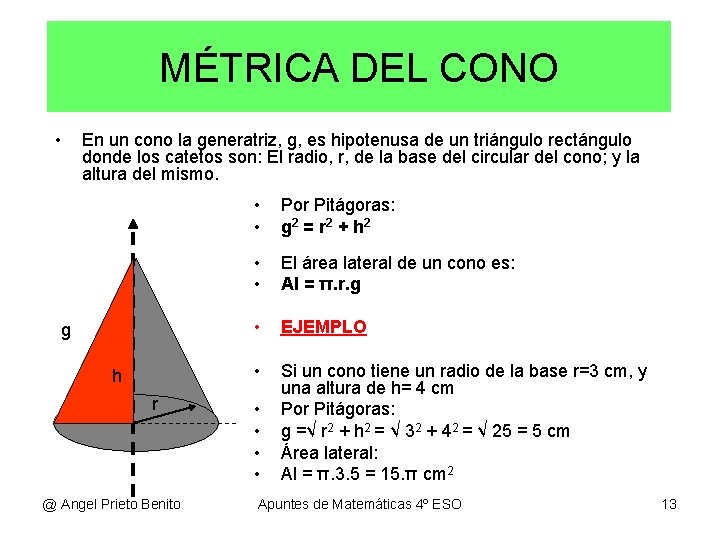
MÉTRICA DEL CONO • En un cono la generatriz, g, es hipotenusa de un triángulo rectángulo donde los catetos son: El radio, r, de la base del circular del cono; y la altura del mismo. g h r @ Angel Prieto Benito • • Por Pitágoras: g 2 = r 2 + h 2 • • El área lateral de un cono es: Al = π. r. g • EJEMPLO • Si un cono tiene un radio de la base r=3 cm, y una altura de h= 4 cm Por Pitágoras: g =√ r 2 + h 2 = √ 32 + 42 = √ 25 = 5 cm Área lateral: Al = π. 3. 5 = 15. π cm 2 • • Apuntes de Matemáticas 4º ESO 13

Ejemplo_1 • El radio de la base de un cono mide 5 cm menos que la altura del cono, y la generatriz 7 cm. Hallar la altura del cono y el área lateral. • Sabemos que en el cono: • • • Operando: 49 = h 2 – 10. h + 25 + h 2 2. h 2 – 10. h – 24 = 0 Simplificando: h 2 – 5. h – 12 = 0 Resolviendo la ecuación: h = [(5 + √ (25 + 48)] / 2 = 6, 75 cm • El radio de la base es: r = h – 5 = 6, 75 – 5 = 1, 75 cm • • • El área lateral es: g 2 = r 2 + h 2 72 = (h - 5)2 + h 2 Al = π. r. g = π. r. √ (h 2 + r 2 ) Al = π. 1, 75. √ (6, 752 + 1, 752 ) = π. 1, 75. 7 = 12, 25. π cm 2 @ Angel Prieto Benito Apuntes de Matemáticas 4º ESO 14

Ejemplo_2 • El radio de la base de un cono mide 5 cm. Hallar la altura para que el área lateral sea igual al área de la base. • • • El área de la base es: Ab = π. r 2 = π. 52 = 25 π cm 2 El área lateral es: Al = π. r. g = 5. π. g Igualando ambas: 25. π = 5. π. g g=5 • Conocidas la generatriz y el radio de la base, por el T. de Pitágoras hallamos la altura: • • • h = √ (g 2 - r 2 ) • IMPORTANTE: En un cono el área lateral es SIEMPRE MAYOR que el área de la base. h = √ (52 – 52) = 0 El cono es imposible, pues para que se cumpla la condición del enunciado la altura sería nula, y por tanto no existe cono alguno. @ Angel Prieto Benito Apuntes de Matemáticas 4º ESO 15