Two approximate approaches for solving the largescale shell

Two approximate approaches for solving the large-scale shell model problem Sevdalina S. Dimitrova Institute for Nuclear Research & Nuclear Energy Bulgarian Academy of Sciences

Collaborators n DMRG n ISA Jorge Dukelsky Nicola Lo Iudice Instituto de Estructura de la Materia, Madrid, Spain University of Naples, Italy Stuart Pittel Antonio Porrino Bartol Research Institute, University of Delaware, USA University of Naples, Italy Mario Stoitsov Francesco Andreozzi Institute for Nuclear Research & Nuclear Energy, Sofia University of Naples, Italy Davide Bianco University of Naples, Italy

Contains n n Large - scale shell model Density matrix renormalization group method Importance sampling algorithm Calculations for 48 Cr in the fp-shell

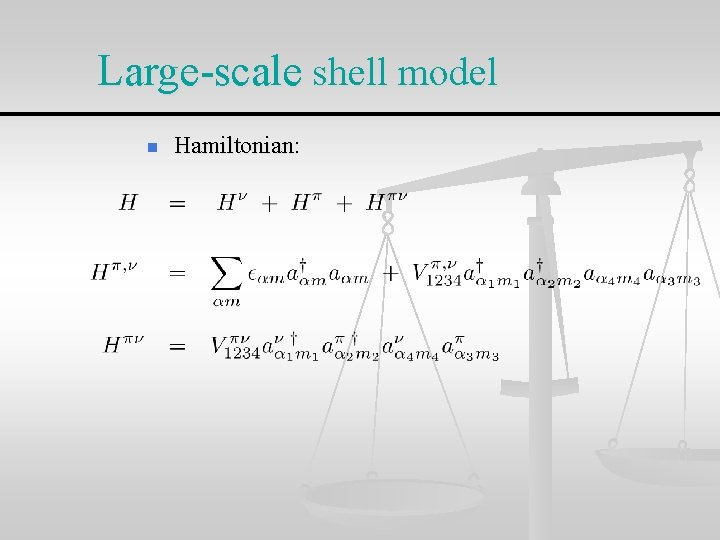
Large-scale shell model n Hamiltonian:

Configuration space n fp -shell

DMRG n Goal of the project: n n Background: n n n Develop the Density Matrix Renormalization Group (DMRG) method for use in nuclear structure; DMRG method introduced by Steven White in 1992 as an improvement of Ken Wilson’s Renormalization Group; Used extensively in condensed matter physics and quantum chemistry; DMRG principle: n n Systematically take into account the physics of all single-particle levels: Still the ordering of the single-particle levels plays a crucial role for the convergence of the calculations;

DMRG n n Q: How to construct optimal approximation to the ground state wave function when we only retain certain number of particle and hole states? A: n Choose the states that maximize the overlap between the truncated state and the exact ground state. Q: How to do this? A: n Diagonalize the Hamiltonian n Define the reduced density matrices for particles and holes

DMRG n Diagonalize these matrices: P, H represent the probability of finding a particular -state in the full ground state wave function of the system; Optimal truncation corresponds to retaining a fixed number of eigenvectors that have largest probability of being in ground state, i. e. , have largest eigenvalues; n Bottom line: DMRG is a method for systematically building in correlations from all single-particle levels in problem. As long as convergence is sufficiently rapid as a function of number of states kept, it should give an accurate description of the ground state of the system, without us ever having to diagonalize enormous Hamiltonian matrices;

DMRG n Subtleties: n Must calculate matrix elements of all relevant operators at each step of the procedure. n This makes it possible to set up an iterative procedure whereby each level can be added straightforwardly. Must of course rotate set of stored matrix elements to optimal (truncated) basis at each iteration. n Procedure as described guarantees optimization of ground state. To get optimal description of many states, we may need to construct mixed density matrices, namely density matrices that simultaneously include info on several states of the system.

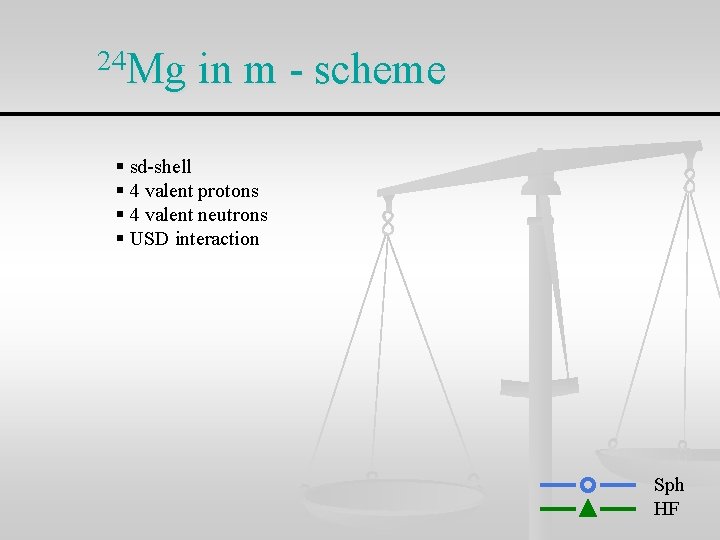
24 Mg in m - scheme § sd-shell § 4 valent protons § 4 valent neutrons § USD interaction Sph HF

Importance Sampling n n F. Andreozzi, A. Porrino and N. Lo Iudice, “A simple iterative algorithm for generating selected eigenspaces of large matrices” J. Phys. A: 35 (2002) L 61–L 66 an iterative algorithm for determining a selected set of eigenvectors of a large matrix, robust and yielding always to ghost-free stable solutions; algorithm with an importance sampling for reducing the sizes of the matrix, in full control of the accuracy of the eigensolutions;

Importance Sampling eigenvalue problem of general form n the iterative dialgonalization algorithm : H= f Hi j g = f hi j H^ j j i g j i i ; j j i = § zero approximation loop: loop f j 1 i ; j 2 i ; : : : ; j N i g f Hi j g (i ; j = 1; 2) §diagonalize the two-dimensional matrix §select the lowest eigenvalue and the corresponding eigenvector: ¸ 2 ; j Á2 i = c(12) j 1 i + c(22) j 2 i ; §µdiagonalize the ¶two-dimensional matrix ¸ j ¡ 1 bj wher e bj = hÁj ¡ 1 j H^ j j i f or j = 3; : : : ; N bj Hj j §select the lowest eigenvalue and the corresponding eigenvector ………. §approximate eigenvalue and eigenvector P N (N ) 1) 1) ( ( = E ´ ¸ N ; j à i ´ j ÁN i c j ii i= 1 i

Importance Sampling n the importance sampling algorithm § start with m basis (m >v) vectorsfand the m. Hi j diagonalize g (i ; j = 1; m) dimensional principal submatrix § for j = v+1, …N diagonalize the v+1 -dimensional matrix : Ã ! ~b ¤ j v ~b = f b ; : : : ; b g H= ; wher e j vj 1 j 2 j ~b. T H jj j ¸ 0 i; (i = 1; v) §select the lowest eigenvalues P state only if j ¸ 0 i ¡ ¸ i j> ² i = 1; v and accept the new §When the truncated configuration space is determined, apply the iterative diagonalization algorithm

Importance Sampling n n n The algorithm has been shown to be completely equivalent to the method of optimal relaxation of I. Shavitt and has therefore a variational foundation; It can be proven that the approximate solution of the eigenvalue problem converges to the exact one; A generalization to calculate several eigenvalues and eigenvectors is straightforward

48 Cr in the fp shell: j-scheme

48 Cr in the fp shell: m-scheme · E = E 0 + A exp ¡ N c ¸

48 Cr in the fp shell: m-scheme

48 Cr in the fp shell: m-scheme

48 Cr: m-scheme in the fp shell J¼ "D M RG "H F + D M RG " I SA " ex act 0+ 2+ 4+ -32. 249 -31. 650 -31. 149 -32. 840 -32. 016 -31. 668 -32. 913 -32. 098 -31. 111 -32. 953 -32. 148 -31. 128

Conclusions: • The first calculations within the ISA in the m-scheme prove the applicability of the method to large-scale shell-model problems. • The DMRG is also a practical approach which needs more tuning. • At it is, the ISA code requires a lot of disk space for considering 56 Ni for example. • At it is, the DMRG code requires large RAM memory to describe heavier nuclei. • Both methods are applicable for odd mass nuclei as well.