Traveling Salesman Problems Repetitive NearestNeighbor and CheapestLink Algorithms

Traveling Salesman Problems Repetitive Nearest-Neighbor and Cheapest-Link Algorithms Chapter: 6

Repetitive Nearest-Neighbor Algorithm • Let A be any vertex. Apply the nearest-neighbor algorithm using A as the starting vertex and calculate the total cost associated with the circuit. • Repeat the process using each of the other vertices (B, C, D, E) of the graph as the staring vertex. • Keep the best one from all the Hamilton circuits. If there is a designated starting vertex, rewrite this circuit with that vertex as the reference point.

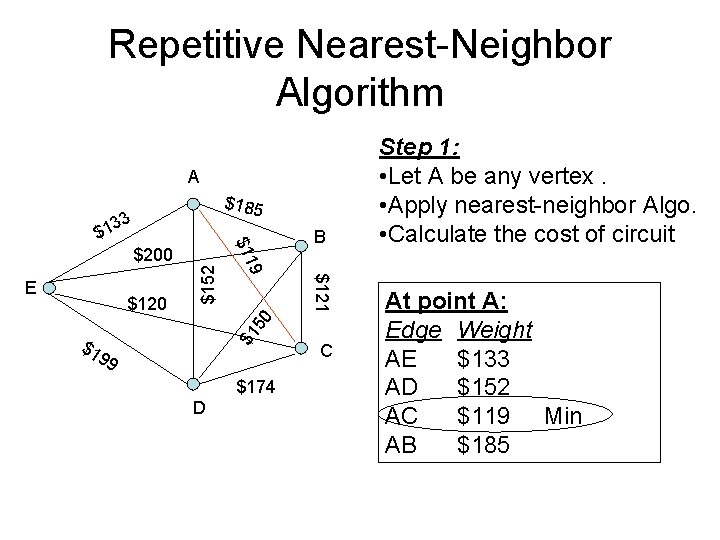
Repetitive Nearest-Neighbor Algorithm A $185 3 B $1 50 $121 $120 9 E $152 $200 $11 3 $1 $1 99 $174 D C Step 1: • Let A be any vertex. • Apply nearest-neighbor Algo. • Calculate the cost of circuit At point A: Edge Weight AE $133 AD $152 AC $119 Min AB $185

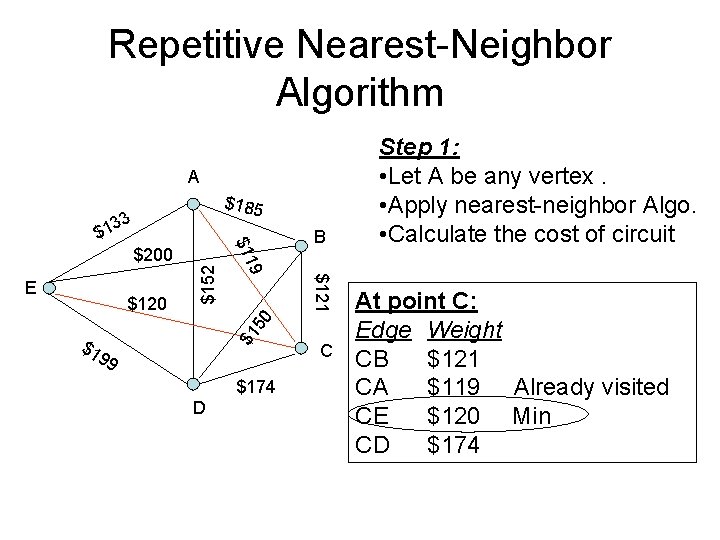
Repetitive Nearest-Neighbor Algorithm A $185 33 B $1 50 $121 $120 9 E $152 $200 $11 $1 $1 99 $174 D C Step 1: • Let A be any vertex. • Apply nearest-neighbor Algo. • Calculate the cost of circuit At point C: Edge Weight CB $121 CA $119 Already visited CE $120 Min CD $174

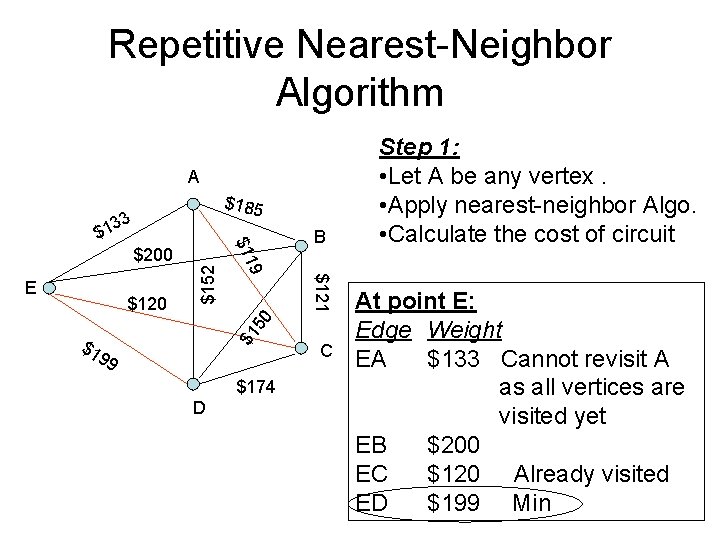
Repetitive Nearest-Neighbor Algorithm A $185 33 B $1 50 $121 $120 9 E $152 $200 $11 $1 $1 99 $174 D C Step 1: • Let A be any vertex. • Apply nearest-neighbor Algo. • Calculate the cost of circuit At point E: Edge Weight EA $133 Cannot revisit A as all vertices are visited yet EB $200 EC $120 Already visited ED $199 Min

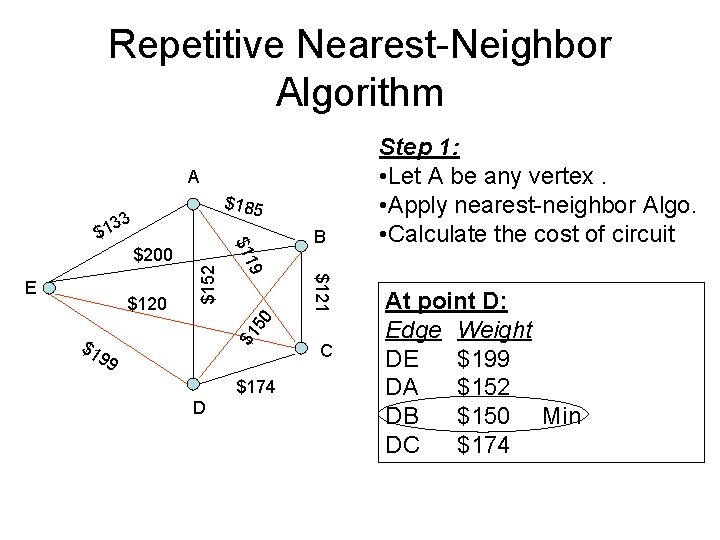
Repetitive Nearest-Neighbor Algorithm A $185 33 B $1 50 $121 $120 9 E $152 $200 $11 $1 $1 99 $174 D C Step 1: • Let A be any vertex. • Apply nearest-neighbor Algo. • Calculate the cost of circuit At point D: Edge Weight DE $199 DA $152 DB $150 Min DC $174

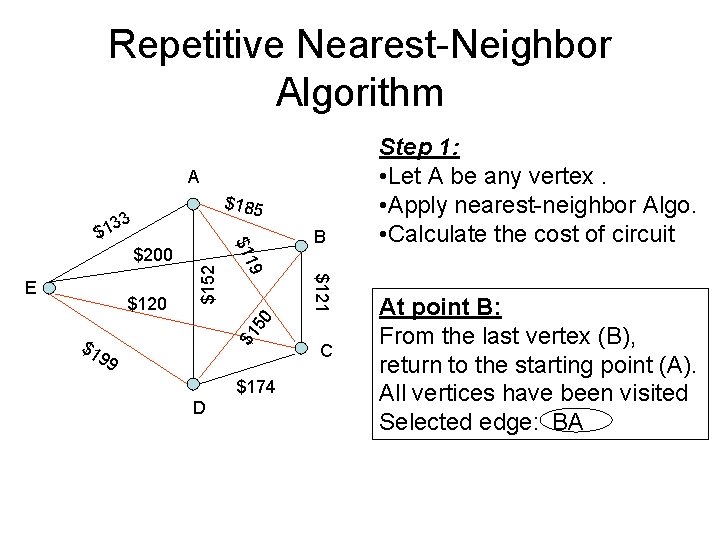
Repetitive Nearest-Neighbor Algorithm A $185 33 B $1 50 $121 $120 9 E $152 $200 $11 $1 $1 99 $174 D C Step 1: • Let A be any vertex. • Apply nearest-neighbor Algo. • Calculate the cost of circuit At point B: From the last vertex (B), return to the starting point (A). All vertices have been visited Selected edge: BA

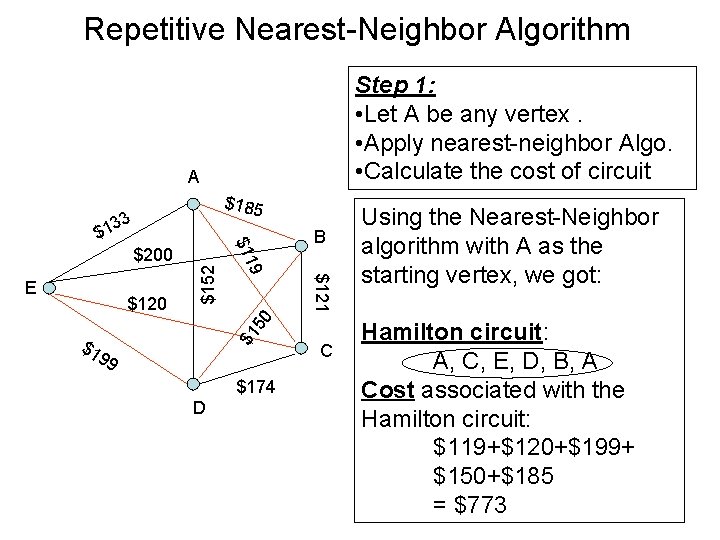
Repetitive Nearest-Neighbor Algorithm Step 1: • Let A be any vertex. • Apply nearest-neighbor Algo. • Calculate the cost of circuit A $185 33 B $1 50 $121 $120 9 E $152 $200 $11 $1 $1 99 $174 D C Using the Nearest-Neighbor algorithm with A as the starting vertex, we got: Hamilton circuit: A, C, E, D, B, A Cost associated with the Hamilton circuit: $119+$120+$199+ $150+$185 = $773

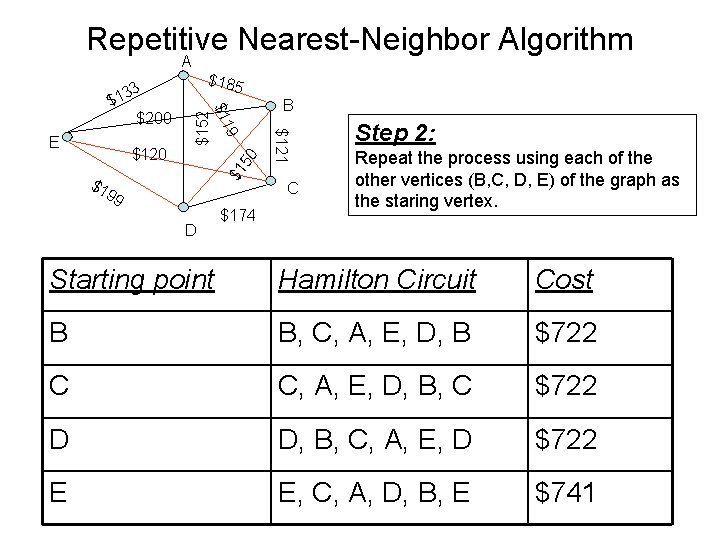
Repetitive Nearest-Neighbor Algorithm A $185 50 $1 $1 99 D $174 B $121 $120 9 E $200 $152 $ $11 3 13 C Step 2: Repeat the process using each of the other vertices (B, C, D, E) of the graph as the staring vertex. Starting point Hamilton Circuit Cost B B, C, A, E, D, B $722 C C, A, E, D, B, C $722 D D, B, C, A, E, D $722 E E, C, A, D, B, E $741

Repetitive Nearest-Neighbor Algorithm A $152 50 $1 $1 99 D $121 $120 9 E $200 B $11 $1 $185 33 C Step 3: • Keep the best one from all the Hamilton circuits. If there is a designated starting vertex, rewrite this circuit with that vertex as the reference point. $174 Starting point Hamilton Circuit Cost A A, C, E, D, B, A $773 B B, C, A, E, D, B $722 C C, A, E, D, B, C $722 D D, B, C, A, E, D $722 E E, C, A, D, B, E $741

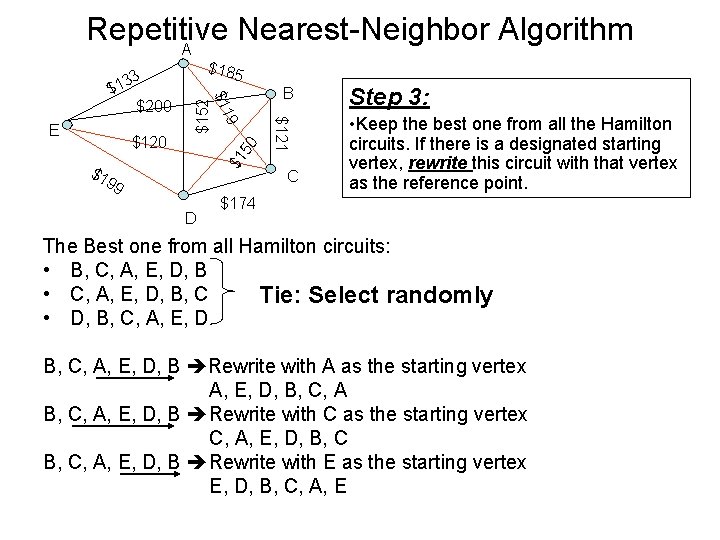
Repetitive Nearest-Neighbor Algorithm A $185 50 $1 $120 $1 99 D B $121 E $200 $152 $ 9 $11 3 13 C Step 3: • Keep the best one from all the Hamilton circuits. If there is a designated starting vertex, rewrite this circuit with that vertex as the reference point. $174 The Best one from all Hamilton circuits: • B, C, A, E, D, B • C, A, E, D, B, C Tie: Select randomly • D, B, C, A, E, D, B Rewrite with A as the starting vertex A, E, D, B, C, A, E, D, B Rewrite with C as the starting vertex C, A, E, D, B, C, A, E, D, B Rewrite with E as the starting vertex E, D, B, C, A, E

Cheapest-Link Algorithm A $185 33 $1 50 $152 $1 99 D B $121 $120 9 E $200 $11 $1 C $174 • Pick the edge with the smallest weight first. Mark the edge (say in red). • Pick the next “cheapest” edge and mark the edge in red. • Continue picking the “cheapest” edge available and mark the edge in red except when – It closes a circuit – It results in three edges coming out of a single vertex • When there are no more vertices to join, close the red circuit.

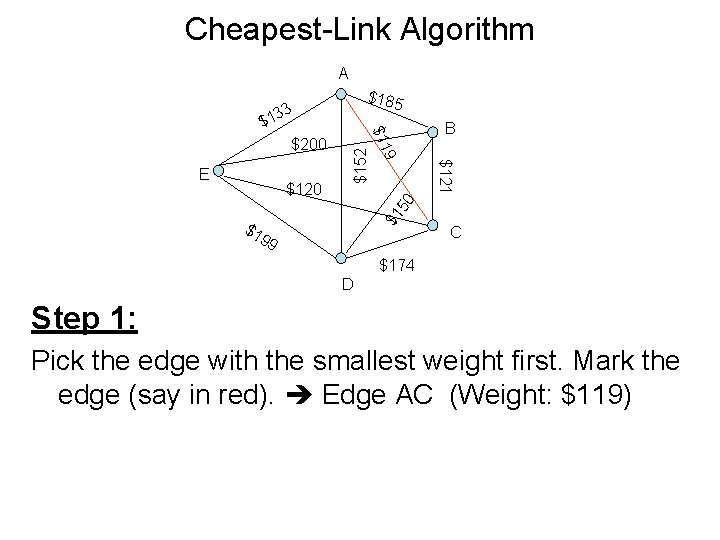
Cheapest-Link Algorithm A $185 33 B $1 50 $121 $120 9 E $152 $200 $11 $1 $1 99 C $174 D Step 1: Pick the edge with the smallest weight first. Mark the edge (say in red). Edge AC (Weight: $119)

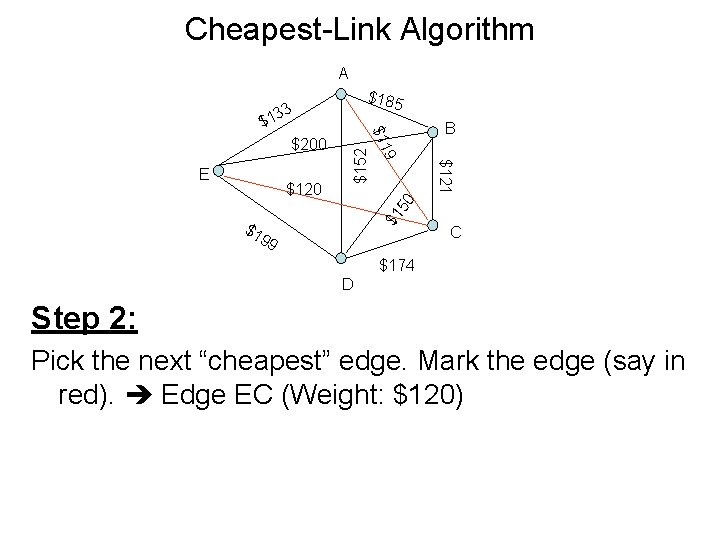
Cheapest-Link Algorithm A $185 33 B $1 50 $121 $120 9 E $152 $200 $11 $1 $1 99 C $174 D Step 2: Pick the next “cheapest” edge. Mark the edge (say in red). Edge EC (Weight: $120)

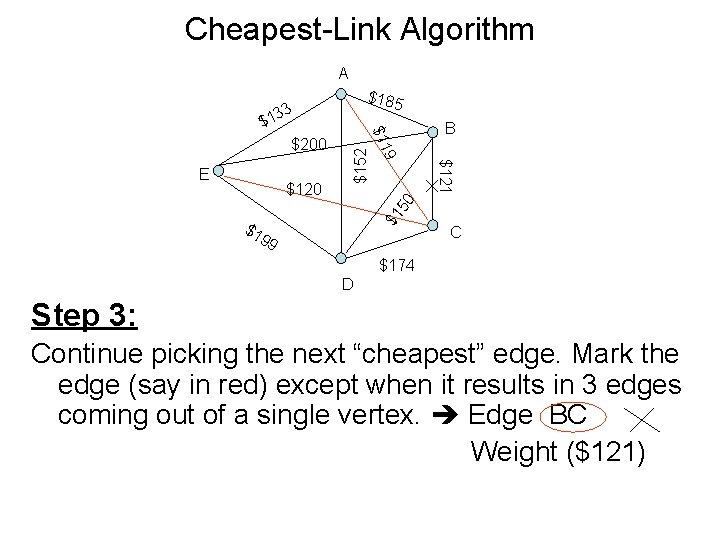
Cheapest-Link Algorithm A $185 33 B $1 50 $121 $120 9 E $152 $200 $11 $1 $1 99 C $174 D Step 3: Continue picking the next “cheapest” edge. Mark the edge (say in red) except when it results in 3 edges coming out of a single vertex. Edge BC Weight ($121)

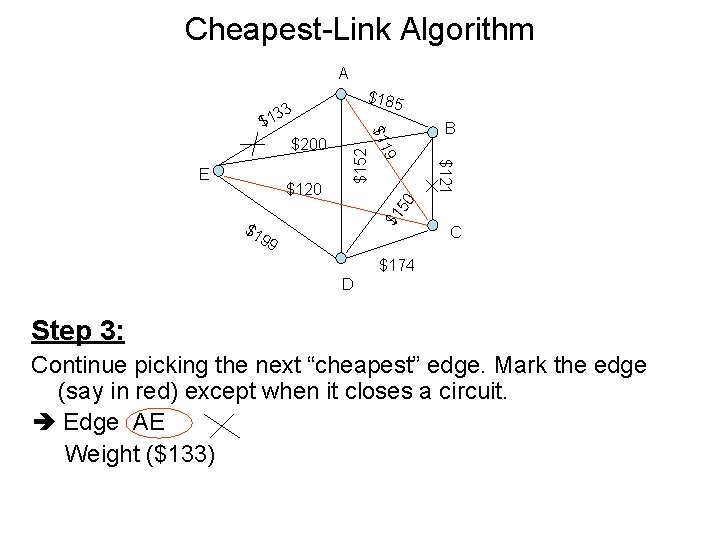
Cheapest-Link Algorithm A $185 33 B $1 50 $121 $120 9 E $152 $200 $11 $1 $1 99 C $174 D Step 3: Continue picking the next “cheapest” edge. Mark the edge (say in red) except when it closes a circuit. Edge AE Weight ($133)

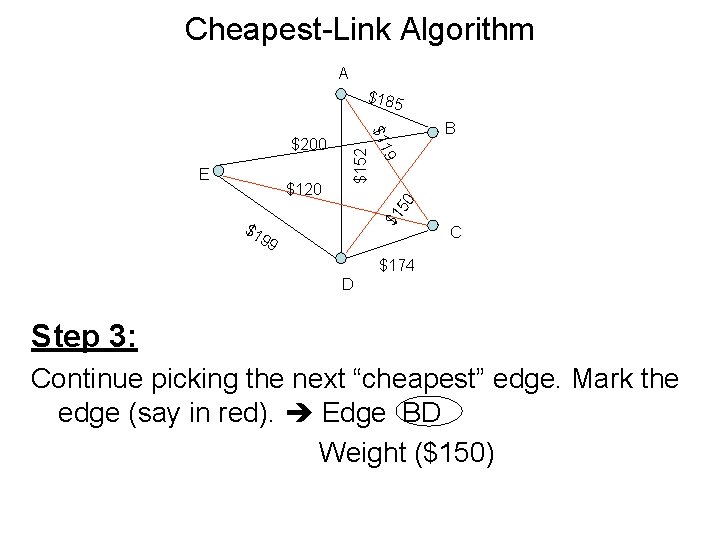
Cheapest-Link Algorithm A $185 $1 50 $152 $120 9 E $11 $200 B $1 99 C $174 D Step 3: Continue picking the next “cheapest” edge. Mark the edge (say in red). Edge BD Weight ($150)

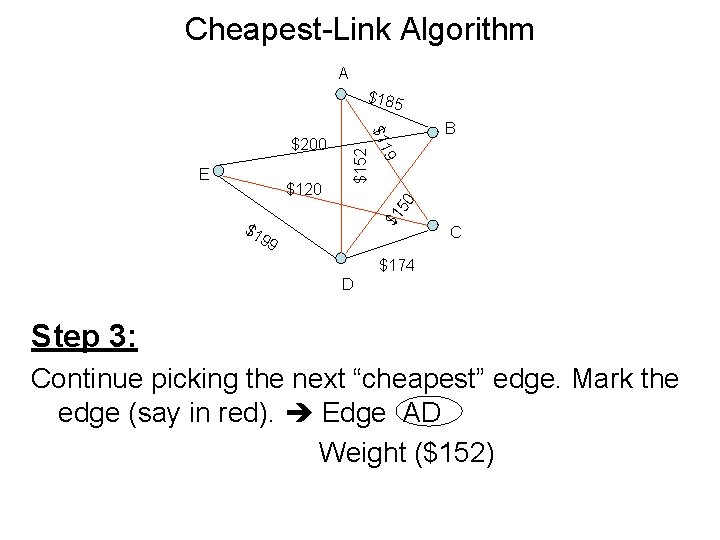
Cheapest-Link Algorithm A $185 $1 50 $152 $120 9 E $11 $200 B $1 99 C $174 D Step 3: Continue picking the next “cheapest” edge. Mark the edge (say in red). Edge AD Weight ($152)

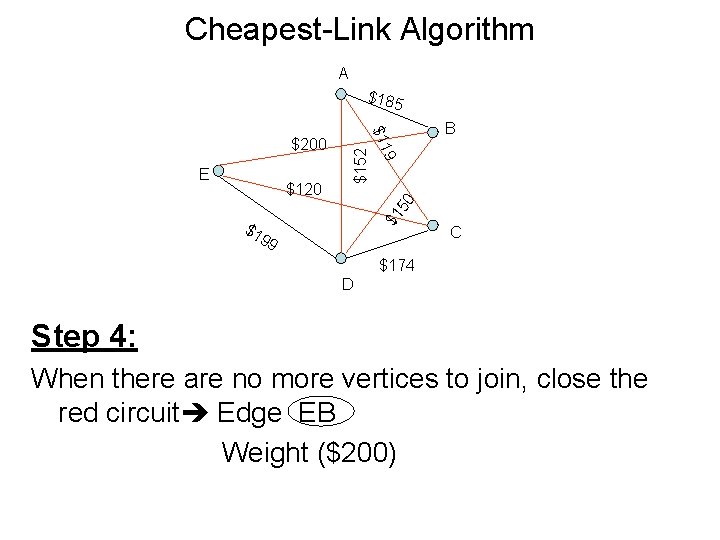
Cheapest-Link Algorithm A $185 $1 50 $152 $120 9 E $11 $200 B $1 99 C $174 D Step 4: When there are no more vertices to join, close the red circuit Edge EB Weight ($200)

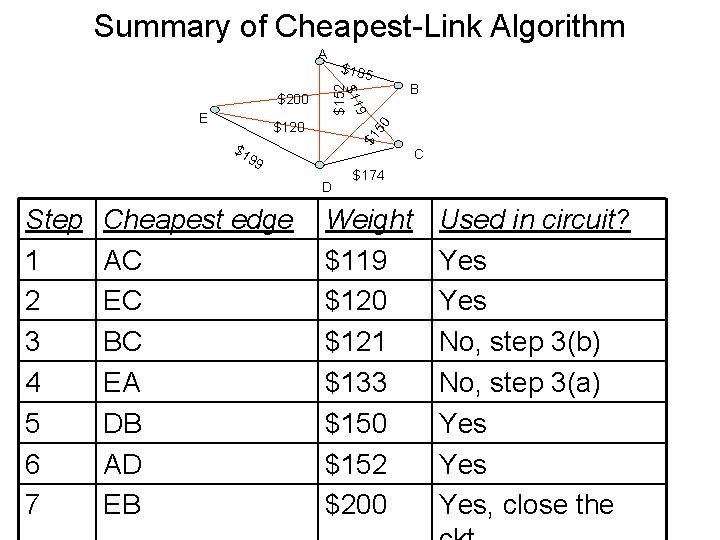
Summary of Cheapest-Link Algorithm A $152 $1 50 $120 $1 C 99 D Step 1 2 3 4 5 6 7 Cheapest edge AC EC BC EA DB AD EB B 9 E $11 $200 $185 $174 Weight $119 $120 $121 $133 $150 $152 $200 Used in circuit? Yes No, step 3(b) No, step 3(a) Yes Yes, close the