The ZigZag Product and Expansion Close to the






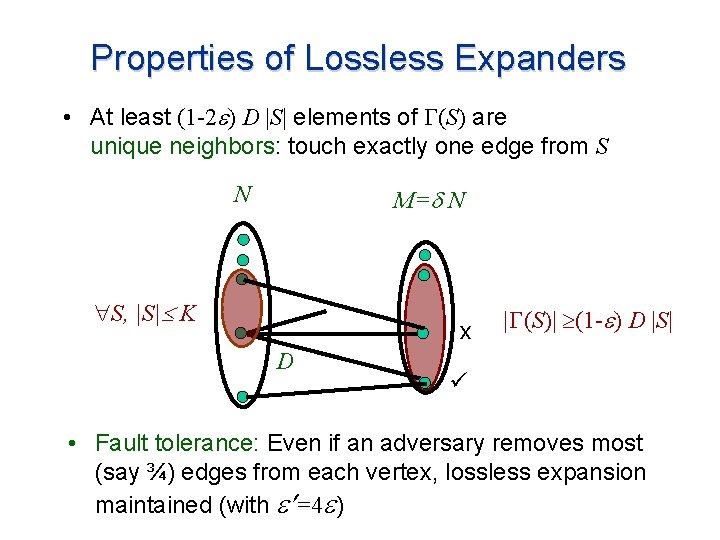




![Randomness Conductors [CRVW 02] N M= N S, |S| K prob. dist. S H(S) Randomness Conductors [CRVW 02] N M= N S, |S| K prob. dist. S H(S)](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-13.jpg)
![Randomness Conductors [CRVW 02] N M= N S, |S| K prob. dist. S H(S) Randomness Conductors [CRVW 02] N M= N S, |S| K prob. dist. S H(S)](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-14.jpg)

![Our Expander Construction • Starting Point: Zig-Zag Graph Product [RVW 00] Compose large graph Our Expander Construction • Starting Point: Zig-Zag Graph Product [RVW 00] Compose large graph](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-16.jpg)

![The Zig-Zag Product [RVW 00] z “Theorem”: Expansion (G 1 z G 2) min(Expansion The Zig-Zag Product [RVW 00] z “Theorem”: Expansion (G 1 z G 2) min(Expansion](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-18.jpg)
![Zig-Zag Analysis (Case I) [RVW 00] Case I: Conditional distributions within “clouds” far fr. Zig-Zag Analysis (Case I) [RVW 00] Case I: Conditional distributions within “clouds” far fr.](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-19.jpg)
![Zig-Zag Analysis (Case II) [RVW 00] Case II: Conditional distributions within clouds uniform. • Zig-Zag Analysis (Case II) [RVW 00] Case II: Conditional distributions within clouds uniform. •](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-20.jpg)
![Zig-Zag for Unbalanced Graphs • Second eigenvalue probably not useful. • Extractors [NZ 93] Zig-Zag for Unbalanced Graphs • Second eigenvalue probably not useful. • Extractors [NZ 93]](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-23.jpg)
![Randomness Conductors [CRVW 02] N M= N S, |S| K prob. dist. S H(S) Randomness Conductors [CRVW 02] N M= N S, |S| K prob. dist. S H(S)](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-24.jpg)


- Slides: 32

The Zig-Zag Product and Expansion Close to the Degree Salil Vadhan Harvard University joint work with Michael Capalbo (DIMACS), Omer Reingold* (Weizmann), and Avi Wigderson (IAS)

Measures of Expansion • Combinatorial: vertex expansion, large cuts • Algebraic: second eigenvalue • Probabilistic: like randomness extractors almost Thm [. . . ]: All equivalent. This talk: • Optimize vertex expansion. • Analysis of zig-zag with extractor-like measure. • Unified entropy-theoretic view of all measures.

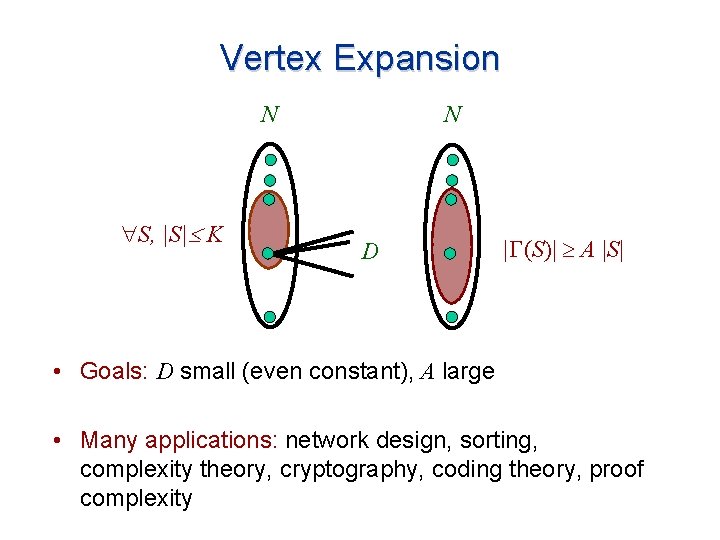
Vertex Expansion N S, |S| K N D | (S)| A |S| • Goals: D small (even constant), A large • Many applications: network design, sorting, complexity theory, cryptography, coding theory, proof complexity

Expander Graphs N S, |S| K N D | (S)| A |S| Q: How large can A be? • Trivial upper bound: A D. • Random graphs: A=D-1. 01 – But many applications need explicit (deterministic & efficient) constructions. • Previously, best explicit expanders: A =D/2 (for constant D and K= (N)).

This Work: Constant-Degree “Lossless” Expanders … which may even be unbalanced: N S, |S| K M= N D | (S)| (1 - ) D |S| 0< , 1 constants D constant & K= (N) For the experts: K= ( M/D) & D= poly(1/ , log (1/ )) (fully explicit: D= quasipoly(1/ , log (1/ )))

Previous explicit constructions • Celebrated sequence of algebraic constructions [Mar 73, GG 80, JM 85, LPS 86, AGM 87, Mar 88, Mor 94, . . . ]. • Achieved optimal 2 nd eigenvalue (Ramanujan graphs), but this only implies vertex expansion D/2 [Kah 95]. • “Combinatorial” constructions: Ajtai [Ajt 87], more explicit and simple [RVW 00]. • “Lossless objects”: [Alo 95, RR 99, TUZ 01] • Unique neighbor, constant-degree expanders [Cap 01].

Why Bother with the Deg. /2 Barrier? • For most applications of expanders: the more expansion the better. • Specific applications for lossless expanders: – Distributed routing in networks [PU 89, ALM 96, BFU 99]. – Expander codes [Gal 63, Tan 81, SS 96, Spi 96, LMSS 01]. – “Bitprobe complexity” of storing subsets [BMRS 00]. – Distributed storage schemes [UW 87]. – Hard tautologies for various proof systems [BW 99, ABRW 00, AR 01].
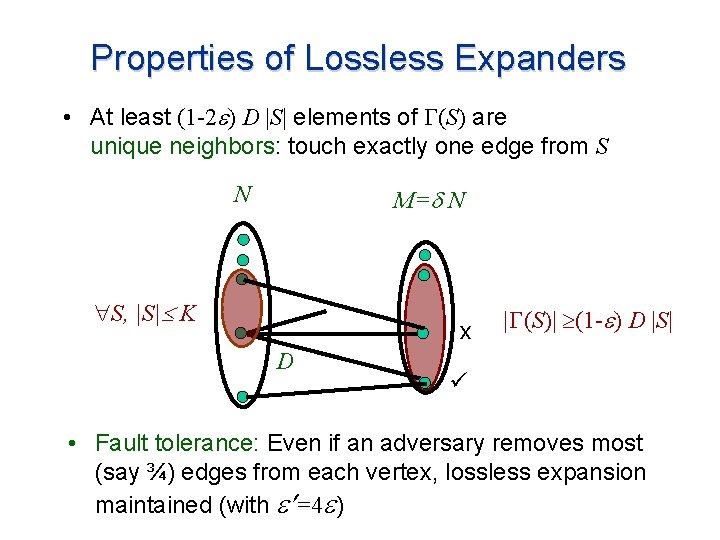
Properties of Lossless Expanders • At least (1 -2 ) D |S| elements of (S) are unique neighbors: touch exactly one edge from S N M= N S, |S| K x D | (S)| (1 - ) D |S| ü • Fault tolerance: Even if an adversary removes most (say ¾) edges from each vertex, lossless expansion maintained (with =4 )

Outline ü Overview & results • Entropy view of expansion • The original zig-zag product & its limitation • The new zig-zag product for conductors

Entropy View of Expansion N M= N S, |S| K prob. dist. S H(S) k | (S)| A |S| D H(induced dist) H(S)+a (A=2 a, B=2 b, . . . ) • Think of expanders as “entropy increasers” – H(X) = number of bits of “randomness” in X – H(X) log 2|Support(X)| w/equality if X uniform on Support(X) – H(XY)= H(X) + H(Y) if X, Y independent

Entropy View of Vertex Expansion N M= N S, |S| K prob. dist. S H(S) k | (S)| A |S| D (A=2 a, B=2 b, . . . ) • Use: H(X)=log 2|Support(X)| H(S ) H(S)+a

Entropy View of 2 nd E-Value N M= N S, |S| K prob. dist. S H(S) k (A=2 a, B=2 b, . . . ) • Use: • Fact: | (S)| A |S| D H(S ) H(S)+a
![Randomness Conductors CRVW 02 N M N S S K prob dist S HS Randomness Conductors [CRVW 02] N M= N S, |S| K prob. dist. S H(S)](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-13.jpg)
Randomness Conductors [CRVW 02] N M= N S, |S| K prob. dist. S H(S) k | (S)| A |S| D (A=2 a, B=2 b, . . . ) • Use: • Allow statistical distance on output H(S ) H(S)+a
![Randomness Conductors CRVW 02 N M N S S K prob dist S HS Randomness Conductors [CRVW 02] N M= N S, |S| K prob. dist. S H(S)](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-14.jpg)
Randomness Conductors [CRVW 02] N M= N S, |S| K prob. dist. S H(S) k | (S)| A |S| D H(S ) H(S)+a (A=2 a, B=2 b, . . . ) • Special Cases: – k+a = m randomness extractors [NZ 93] – a= d lossless expanders [RR 99, TUZ 01]

Entropy View of Expansion N M= N S, |S| K prob. dist. S H(S) k | (S)| A |S| D H(induced dist) H(S)+a (A=2 a, B=2 b, . . . ) • Think of expanders as “entropy increasers” – H(X) = number of bits of “randomness” in X – H(X) log 2|Support(X)| w/equality iff X uniform on Support(X) – H(XY)= H(X) + H(Y) if X, Y independent
![Our Expander Construction Starting Point ZigZag Graph Product RVW 00 Compose large graph Our Expander Construction • Starting Point: Zig-Zag Graph Product [RVW 00] Compose large graph](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-16.jpg)
Our Expander Construction • Starting Point: Zig-Zag Graph Product [RVW 00] Compose large graph w/ small graph to obtain a new graph which (roughly) inherits – Size of large graph. – Degree from the small graph. – Expansion from both. • Original motivation: A combinatorial construction of constant-degree expanders with simple analysis.

Outline ü Overview & results ü Entropy view of expansion • The original zig-zag product & its limitation • The new zig-zag product for conductors
![The ZigZag Product RVW 00 z Theorem Expansion G 1 z G 2 minExpansion The Zig-Zag Product [RVW 00] z “Theorem”: Expansion (G 1 z G 2) min(Expansion](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-18.jpg)
The Zig-Zag Product [RVW 00] z “Theorem”: Expansion (G 1 z G 2) min(Expansion (G 2), Expansion (G 1)) – formal versions for 2 nd e-value, extractors [RVW 00]
![ZigZag Analysis Case I RVW 00 Case I Conditional distributions within clouds far fr Zig-Zag Analysis (Case I) [RVW 00] Case I: Conditional distributions within “clouds” far fr.](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-19.jpg)
Zig-Zag Analysis (Case I) [RVW 00] Case I: Conditional distributions within “clouds” far fr. uniform. – First step on small graph adds entropy. – Next two steps can’t lose entropy.
![ZigZag Analysis Case II RVW 00 Case II Conditional distributions within clouds uniform Zig-Zag Analysis (Case II) [RVW 00] Case II: Conditional distributions within clouds uniform. •](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-20.jpg)
Zig-Zag Analysis (Case II) [RVW 00] Case II: Conditional distributions within clouds uniform. • First small step does nothing. • Step on big graph “scatters” among clouds (shifts entropy) • Second small step adds entropy.

Inherent Entropy Loss – In each case, only one of two small steps “works” – But paid for both in degree.

Trying to improve ? ? ? Idea: • Use two “optimal” small graphs. • How to measure? ? ? ?
![ZigZag for Unbalanced Graphs Second eigenvalue probably not useful Extractors NZ 93 Zig-Zag for Unbalanced Graphs • Second eigenvalue probably not useful. • Extractors [NZ 93]](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-23.jpg)
Zig-Zag for Unbalanced Graphs • Second eigenvalue probably not useful. • Extractors [NZ 93] and condensers [RR 99, RSW 00, TUZ 01] work well in unbalanced case. • In fact, [RVW 00] analyzed a zig-zag product for extractors (with an “easier goal”). try to analyze zig-zag for randomness conductors
![Randomness Conductors CRVW 02 N M N S S K prob dist S HS Randomness Conductors [CRVW 02] N M= N S, |S| K prob. dist. S H(S)](https://slidetodoc.com/presentation_image_h2/87c0905850807cfd29412c364126c652/image-24.jpg)
Randomness Conductors [CRVW 02] N M= N S, |S| K prob. dist. S H(S) k | (S)| A |S| D H(S ) H(S)+a (A=2 a, B=2 b, . . . ) • Special Cases: – k+a = m randomness extractors [NZ 93] – a= d lossless expanders [RR 99, TUZ 01]

Outline ü Overview & results ü Entropy view of expansion ü The original zig-zag product & its limitation • The new zig-zag product for conductors

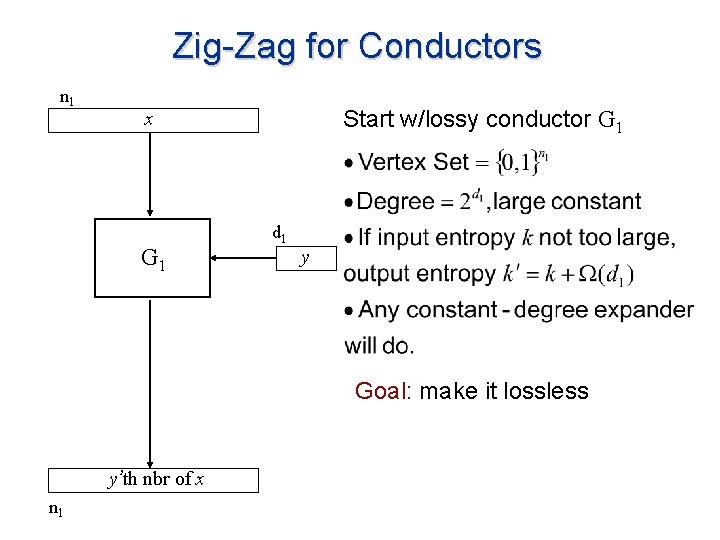
Zig-Zag for Conductors n 1 Start w/lossy conductor G 1 x G 1 d 1 y Goal: make it lossless y’th nbr of x n 1

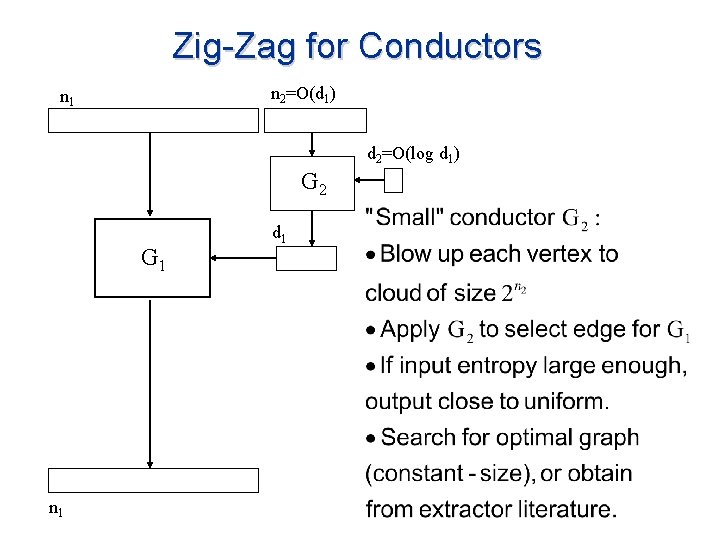
Zig-Zag for Conductors n 2=O(d 1) n 1 d 2=O(log d 1) G 2 G 1 n 1 d 1

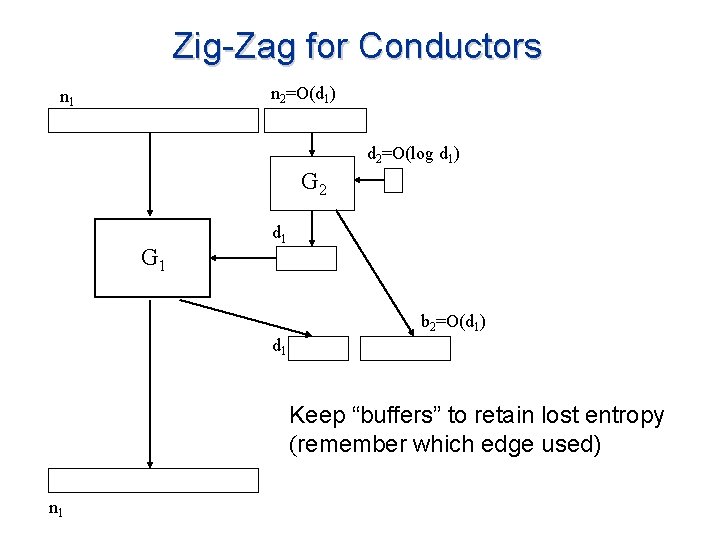
Zig-Zag for Conductors n 2=O(d 1) n 1 d 2=O(log d 1) G 2 G 1 d 1 b 2=O(d 1) d 1 Keep “buffers” to retain lost entropy (remember which edge used) n 1

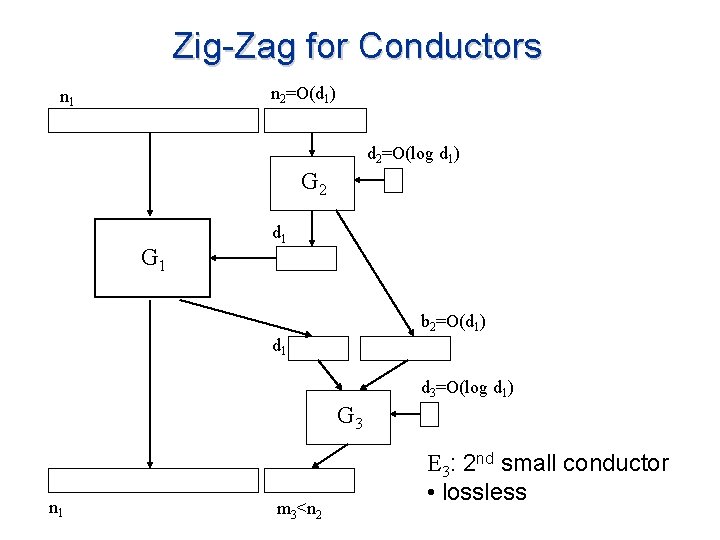
Zig-Zag for Conductors n 2=O(d 1) n 1 d 2=O(log d 1) G 2 G 1 d 1 b 2=O(d 1) d 1 d 3=O(log d 1) G 3 n 1 m 3<n 2 E 3: 2 nd small conductor • lossless

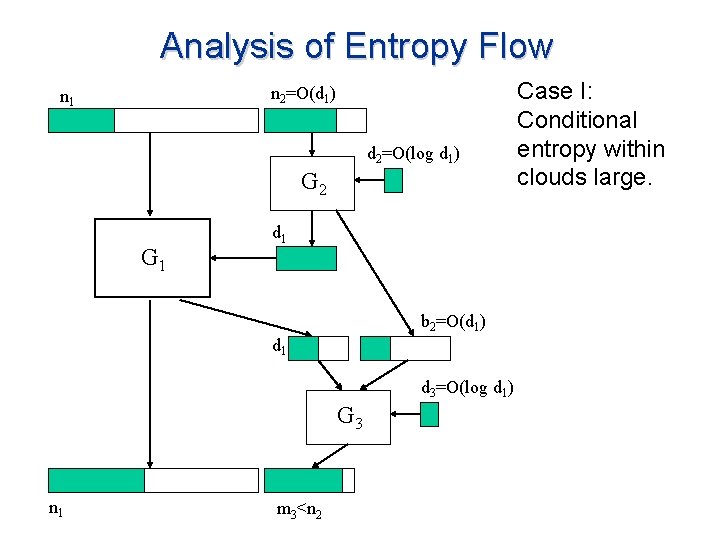
Analysis of Entropy Flow n 2=O(d 1) n 1 d 2=O(log d 1) G 2 G 1 d 1 b 2=O(d 1) d 1 d 3=O(log d 1) G 3 n 1 m 3<n 2 Case I: Conditional entropy within clouds large.

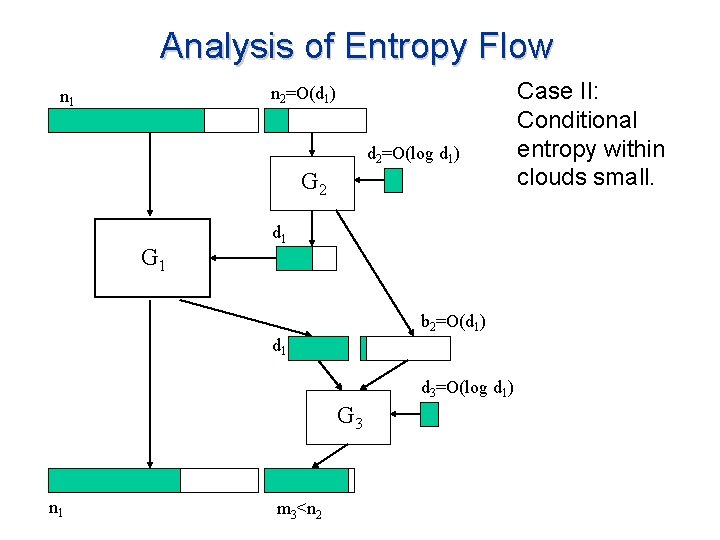
Analysis of Entropy Flow n 2=O(d 1) n 1 d 2=O(log d 1) G 2 G 1 d 1 b 2=O(d 1) d 1 d 3=O(log d 1) G 3 n 1 m 3<n 2 Case II: Conditional entropy within clouds small.

Summary and Open Problems • Our Result: Constant-Degree Lossless Expanders • Main tools: randomness conductors, zig-zag product Further Research: • • Analyze algebraic expanders wrt conductor measure. The undirected case (being lossless from both sides). Better expansion yet? D-O(1) Continue the study of randomness conductors.