The Maxwell equations James Clerk Maxwell 13 June

The Maxwell equations

James Clerk Maxwell (13 June 1831 – 5 November 1879) • Scottish theoretical physicist and mathematician. • The most significant achievements: – the development of the classical electromagnetic theory, synthesizing all previous unrelated observations, experiments and equations of electricity, magnetism and even optics into a consistent theory.

• Scientific career : – – Professor of Aberdeen University Professor of Kings College in London Professor of Cambridge University Founder of Cavendish Laboratory • Scientific disciplines – Molecular physics – Optics – Electrodynamics • Important dates – 1864 – Maxwell’s equations – 1865 – concept of electromagnetic nature of light

James Clerk Maxwell (13 June 1831 – 5 November 1879)

The Maxwell equations Maxwell’s equations are a generalization of all electrostatic and magnetic phenomena known before. Maxwell’s equations express the inseparable relation between electric and magnetic fields. From Maxwell’s equations come directly: • law of energy conservation • law of charge conservation • electromagnetic waves existence and propagation (proved by Hertz in 1886)

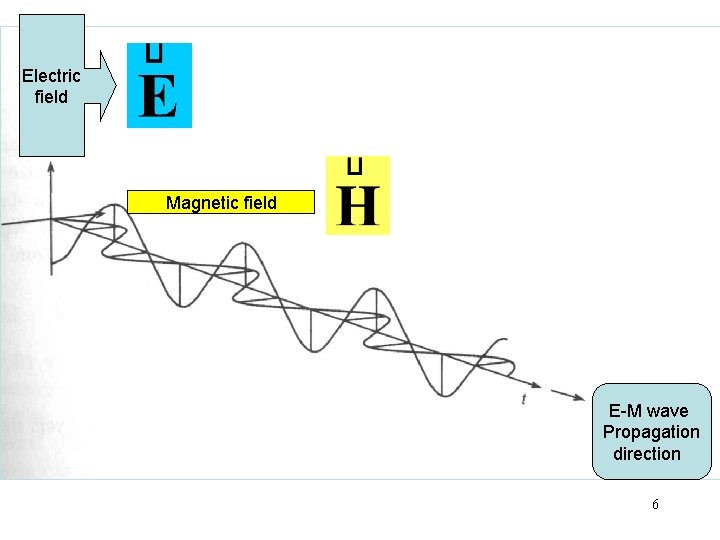
Electromagnetic waves Electric field Magnetic field E-M wave Propagation direction 6

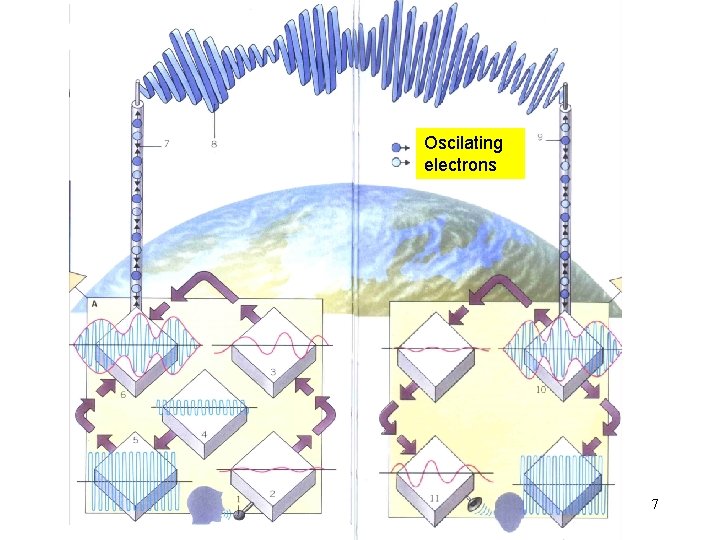
Oscilating electrons Wd. WI 2015 PŁ 7

Maxwell’s equations are the basis of electromagnetism These two equations and additional six equations form a set of 8 equations fully describing electromagnetic field. Three Maxwell’s postulates concerning divergence of the field: So called „point equations” inform us about a medium in which the field exists:

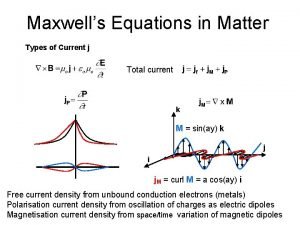
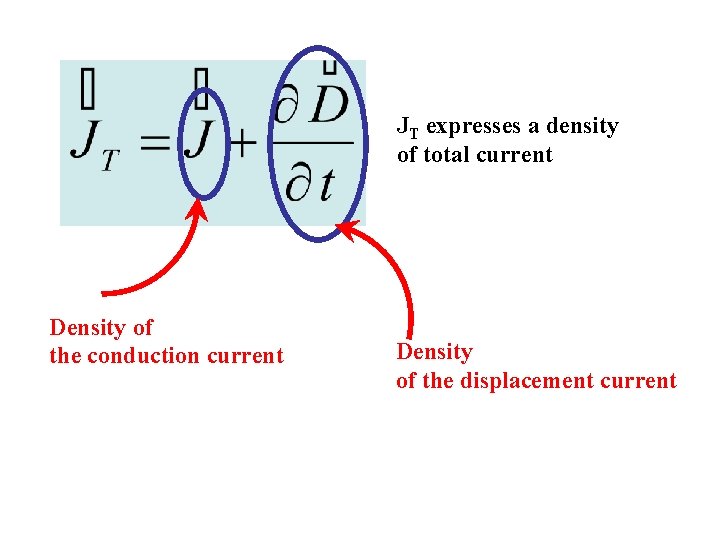
I Maxwell’s equation Differential form of Maxwell’s equation Rotational magnetic field (vortex field) is generated by currents and/or by changing electric field. is the conduction current density The notion is called „density of displacement current”

JT expresses a density of total current Density of the conduction current Density of the displacement current

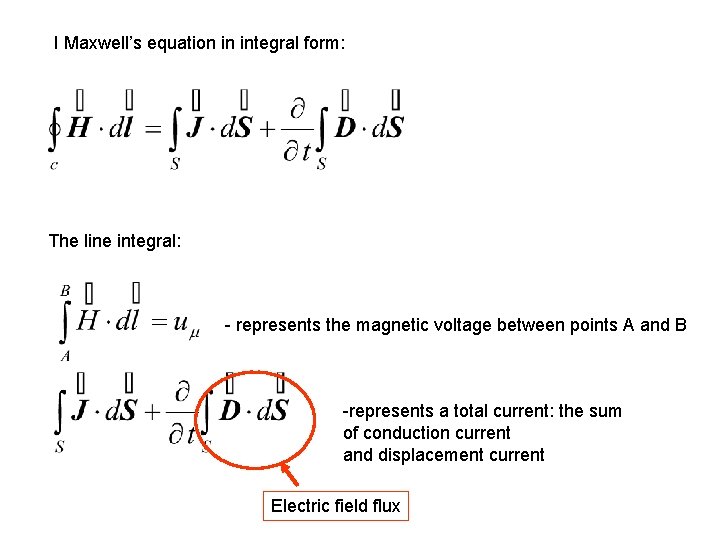
Integral form of I Maxwell’s equation From differential form of Maxwell’s equation after integration over the surface S with the bound c we receive a new form: Stokes theorem The order of operations can be changed, because the integration over the surface and differentiation with respect of time are independent.

I Maxwell’s equation in integral form: The line integral: - represents the magnetic voltage between points A and B -represents a total current: the sum of conduction current and displacement current Electric field flux

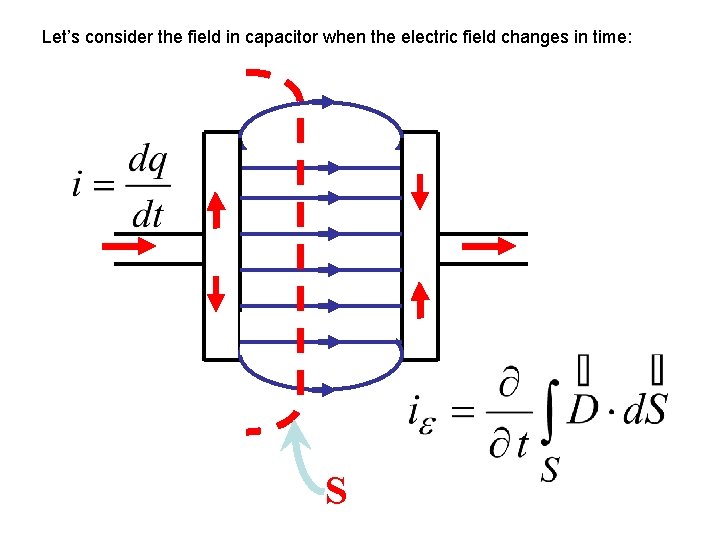
Let’s consider the field in capacitor when the electric field changes in time: S

The conduction current flowing in wires is motion of the charges. Changing electric field exists between the capacitor plates. The electric flux goes through the surface S: Displacement current exists in the capacitor

A displacement current is the extension of current flow in dielectric, where there is no way for conduction current. The rule: the current flows by closed path is realised like this: in wires – a conduction current in dielectric – a displacement current This current can reach great values if the field is changing with great frequency.

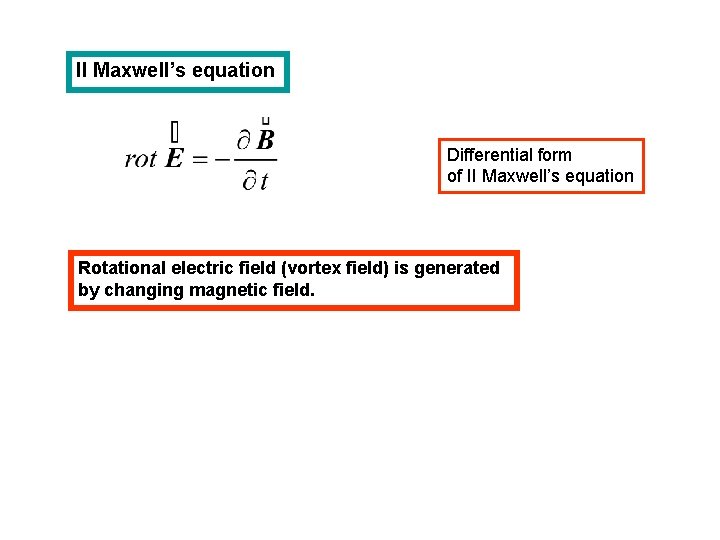
II Maxwell’s equation Differential form of II Maxwell’s equation Rotational electric field (vortex field) is generated by changing magnetic field.

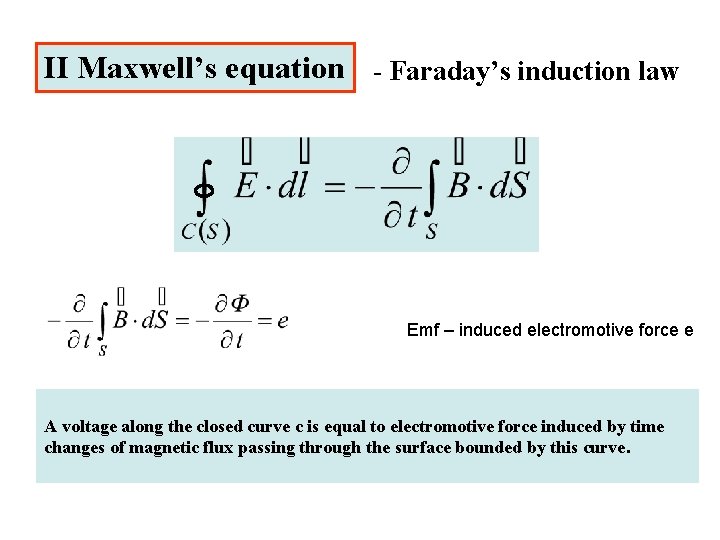
Integral form of II Maxwell’s equation From differential form of II Maxwell’s equation after integration over the surface S with the bound c we receive the integral form: Stokes theorem Magnetic flux

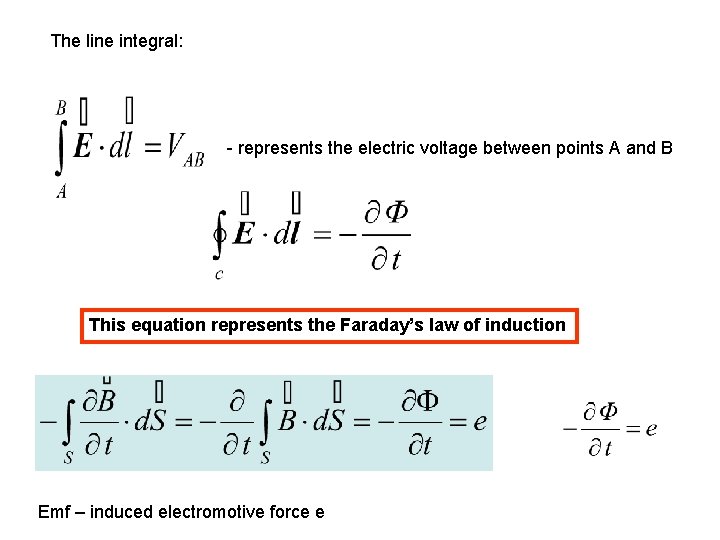
The line integral: - represents the electric voltage between points A and B This equation represents the Faraday’s law of induction Emf – induced electromotive force e

The integral form of Maxwell’s equations

I Maxwell’s equation - Ampère’s law A magnetic voltage along the closed curve c is equal to the total current – the sum of the conduction current and displacement current passing through the surface which bound is the curve c.

II Maxwell’s equation - Faraday’s induction law Emf – induced electromotive force e A voltage along the closed curve c is equal to electromotive force induced by time changes of magnetic flux passing through the surface bounded by this curve.

Wave in an ideal dielectric We will derive the wave equations for electric and magnetic field from Maxwell’s equations. It will be a proof that the electromagnetic field is a wave. Assumptions: 1. Considered area is unlimited 2. Considered medium is linear, homogenous and isotropic 3. γ=0, it means a medium is lossless 3’. There are no currents and no charges in the considered area

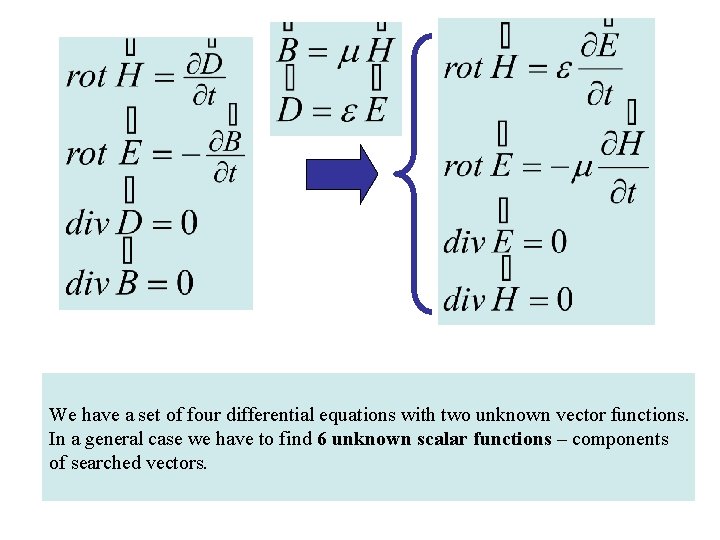
We have a set of four differential equations with two unknown vector functions. In a general case we have to find 6 unknown scalar functions – components of searched vectors.

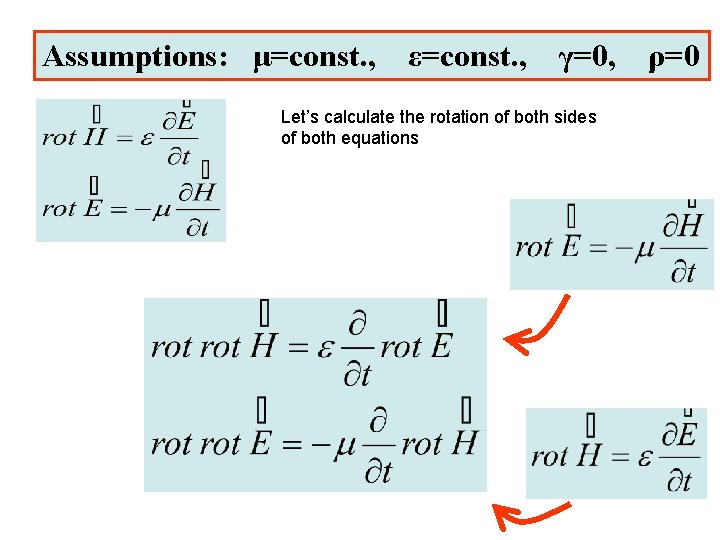
Assumptions: μ=const. , ε=const. , γ=0, Let’s calculate the rotation of both sides of both equations ρ=0

From vector identity: =0 =0

We have received two wave equations. Two vector functions E(P, t) i H(P, t) which satisfy this equations form electromagnetic wave. Attention: This means there might exist such solutions of wave equations which don’t satisfy Maxwell’s equations. Solutions E(P, t) i H(P, t) must satisfy condition coming from Maxwell’s equations.

Three Maxwell’s postulates concerning divergence of the field: and