Stochastic Planning using Decision Diagrams Sumit Sanghai Stochastic

Stochastic Planning using Decision Diagrams Sumit Sanghai

Stochastic Planning • MDP model ? – Finite set of states S – Set of actions A, each having a transition probability matrix – Fully observable – A reward function R associated with each state

Stochastic Planning … • Goal ? – Policy which maximizes the expected total discounted reward in an infinite horizon model – Policy is a mapping from state to action • Problem ? – Total reward can be infinite • Solution ? – Associate a discount factor b

Expected Reward Model • Expected Reward Model – Vp(s) = R(s) + b åt Pr(s, p(s), t) Vp(t) • Optimality ? – Policy p is optimal if Vp >= Vp` for all s and p` • Thm : There exists an optimal policy – Its value function is denoted as V*

Value Iteration • Vn+1(s) = R(s) + maxa b åt Pr(s, a, t) Vn(t) V 0(s) = R(s) • Stopping condition : – if maxs {Vn+1(s) – Vn(s)} < e(1 -b) / 2 b then Vn+1 is e/2 close to V* • Thm : Value Iteration gives optimal policy • Problem ? – Can be slow if state space too large

Boolean Decision Diagrams • Graph Representation of Boolean Functions • BDD = Decision Tree – redundancies – Remove duplicate nodes – Remove any node with both child pointers pointing to the same child

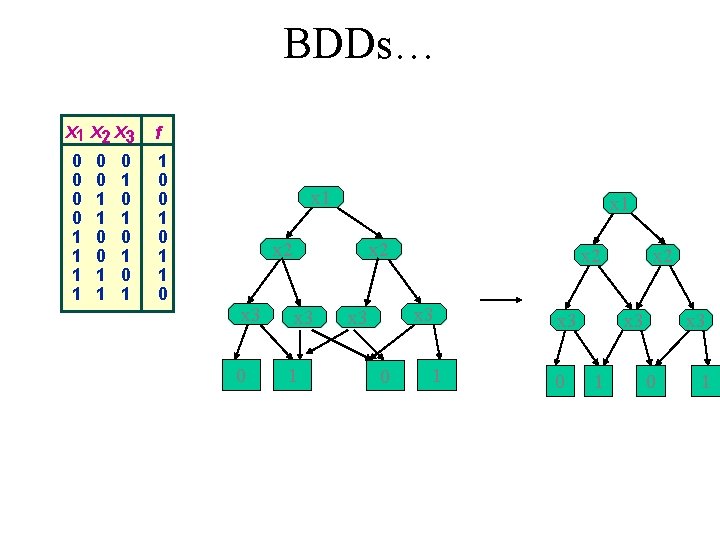
BDDs… x 1 x 2 x 3 0 0 1 1 0 1 0 1 f 1 0 0 1 1 0 x 1 x 2 x 3 0 x 2 x 3 1 x 2 x 3 0 1 x 3 0 x 2 x 3 1 x 3 0 1

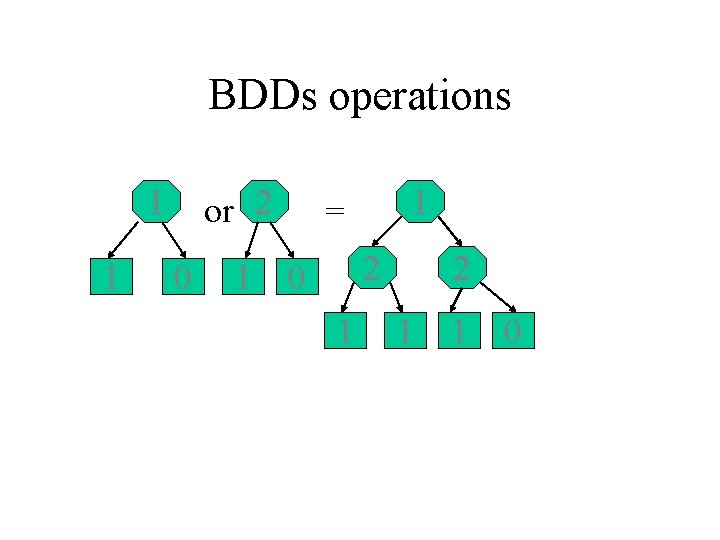
BDDs operations 1 1 or 2 0 1 1 = 2 0 1 2 1 1 0

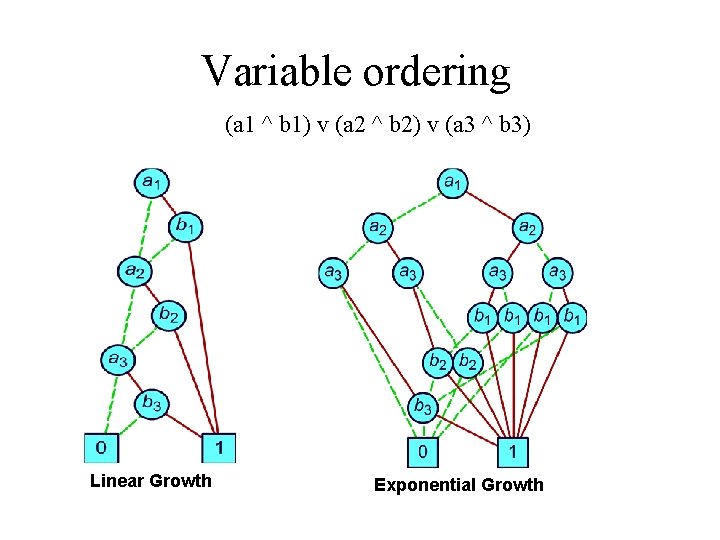
Variable ordering (a 1 ^ b 1) v (a 2 ^ b 2) v (a 3 ^ b 3) Linear Growth Exponential Growth

BDD no magic • Number of boolean functions – 2^{2^n} • With polynomial nodes – Exponential functions

ADDs • BDDs + real valued domain • Useful to represent probabilities

MDP, State Space and ADDs • Factored MDP – S characterized by {X 1, X 2, …, Xn} • Action a from s to s` a from {X 1, X 2, …, Xn} to {X 1`, X 2`, …, Xn`} • Pr(s, a, s`) ? – Pra(Xi`|X 1, X 2, …, Xn) – Each can be represented using ADD

Value Iteration Using ADDs • Vn+1(s) = R(s) + b maxa {åt P(s, a, t) Vn(t)} – R(s) : ADD • P(s, a, t)=Pa(X 1`=x 1`, …, Xn`=xn`|X 1=x 1, …, Xn=xn) = Õi. P(Xi`=xi`|X 1=x 1, …, Xn=xn) Vn+1(X 1, …, Xn) = R(X 1, …Xn) + b maxa {åX 1`, …, Xn` Õi Pa(Xi`|X 1, …, Xn) Vn(X 1`, …, Xn`)} • 2 nd term on RHS can be obtained by quantifying X 1` first as true or false and multiplying its associated ADD with Vn and summing over all possibilities to eliminate X 1` åX 1`, …, Xn` {Õi=2 to n {Pa(Xi`|X 1, …, Xn)} (Pa(X 1`=true|X 1, …, Xn) Vn(X 1`=true, …, Xn`) + Pa(X 1`=false|X 1, …, X_n) Vn(X 1`=false, …, Xn`) )}

Value Iteration Using ADDs (other possibilities) • Which variables are necessary ? – variables appearing in the value function • Order of variables during elimination ? – Inverse order • Problem ? – Repeated computation of Pr(s, a, t) • Solution ? – Precompute Pa(X 1`, …, Xn`|X 1, …, Xn) – Mutliply the dual action diagrams

Value Iteration… • Space vs Time ? – Precomputation : huge space required – No precomputation : time wasted • Solution (do something intermediate) – Divide variables into sets (restriction ? ? ) and precompute for them • Problems with precomputation – Precomputation for sets containing variables which do not appear in value function – Dynamic precomputation

Experiments • Goals ? • SPUDD vs Normal value iteration – What is SPI ? – How is comparison done ? • Worst case of SPUDD • Missing links ? – SPUDD vs Others – Space vs Time experiments

Future Work • • Variable reordering Policy iteration Approximate ADDs Formal model for structure exploitation – BDDs eg. Symmetry detection • First order ADDs

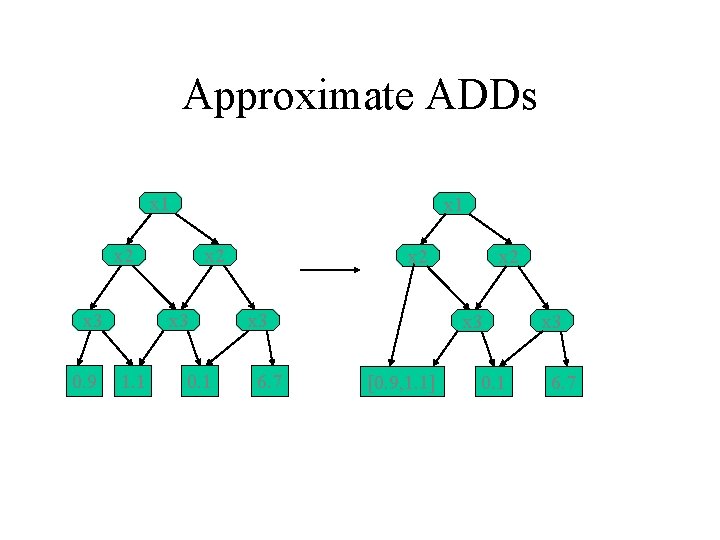
Approximate ADDs x 1 x 2 x 3 0. 9 x 2 x 3 1. 1 0. 1 x 2 x 3 6. 7 x 2 x 3 [0. 9, 1. 1] 0. 1 x 3 6. 7

Approximate ADDs • At each leaf node ? – Range : [min, max] – What value and error do you associate with that leaf ? • How and till when to merge the leaves ? – max_size vs max_error • Max_size mode – Merge closest pairs of leaves till size < max_size • Max_error mode – Merge pairs such that error < max_error

Approximate Value Iteration • Vn+1 from Vn ? – At each leaf node do calculation for both min and max : eg [min 1, max 1]*[min 2, max 2] = [min 1*min 2, max 1*max 2] – What about maxa step ? – Reduce again • When to stop ? – When the ranges for every state in 2 consecutive value functions overlap or lie within some tolerance (e) • How to get policy ? – Find actions which maximize value functions (when range is replaced by midpoints) • Convergence ?

Variable reordering • Intuitive ordering – Variables which are correlated should be placed together • Random – Pick pairs of variables and swap them • Rudell’s sifting – Pick a variable, find a better position • Experiments : Sifting did very well