SSAC 2006 QA 531 LV 1 2 How

SSAC 2006: QA 531. LV 1. 2 How Far is Yonder Mountain? – A Trig Problem Imagine you sight on a distant peak as your wagon train moves toward it day after day. Can you calculate how far away the peak is, and how high it is? Core Quantitative Issue Geometry: Trigonometry, tangent Supporting Quantitative Issues Number sense: Effect of measurement error Algebra, combining equations Algebra, rearranging equations Algebra, finding solutions by trial and error Geometry: circles: radians Prepared for SSAC by Len Vacher – University of South Florida, Tampa FL © The Washington Center for Improving the Quality of Undergraduate Education. All rights reserved. 2005 1

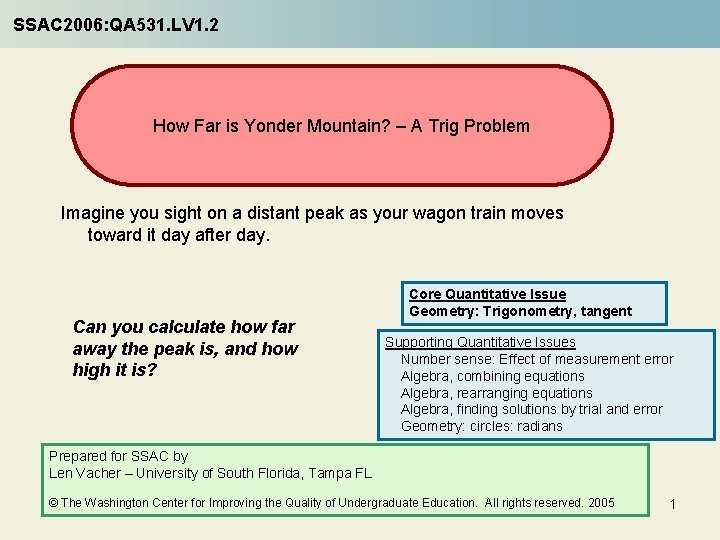
Problem You are on the High Plains, heading west. In the far distance you see a high peak in the Rocky Mountains and head your wagon train straight for it. Yesterday, you carefully used an inclinometer to measure the angle between the horizontal and the line of sight from you to the top of the peak. The angle was 2. 0. Today, you repeat the measurement. The angle is 2. 7. You have traveled 12. 0 miles since yesterday’s measurement. (Imagine) How many miles are you now from the peak? How many feet above you is the peak? (Assume there is no change in elevation between yesterday and today. Assume too that the Earth is flat. ) 2

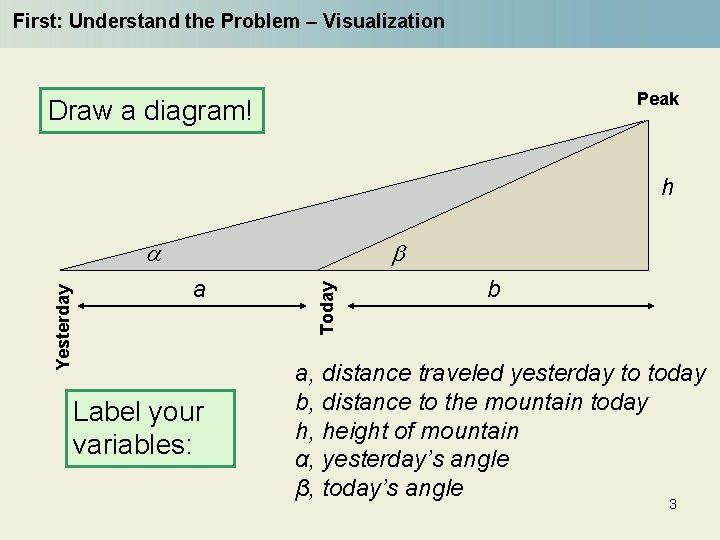
First: Understand the Problem – Visualization Peak Draw a diagram! h b a Label your variables: Today Yesterday a b a, distance traveled yesterday to today b, distance to the mountain today h, height of mountain α, yesterday’s angle β, today’s angle 3

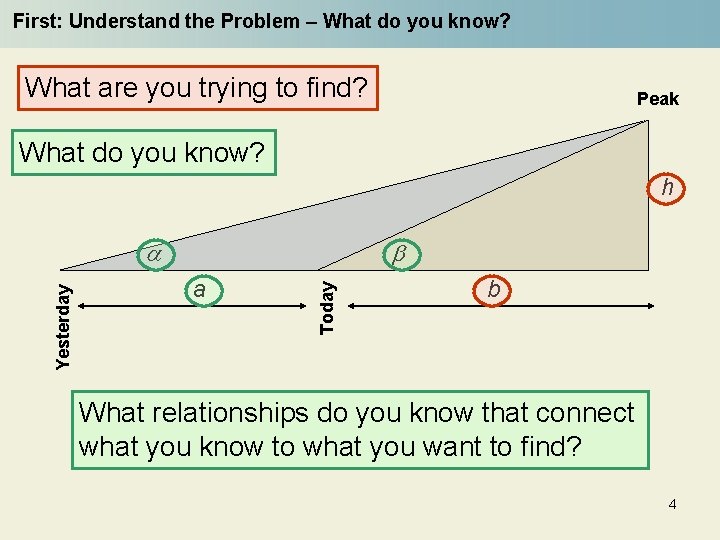
First: Understand the Problem – What do you know? What are you trying to find? Peak What do you know? h b a Today Yesterday a b What relationships do you know that connect what you know to what you want to find? 4

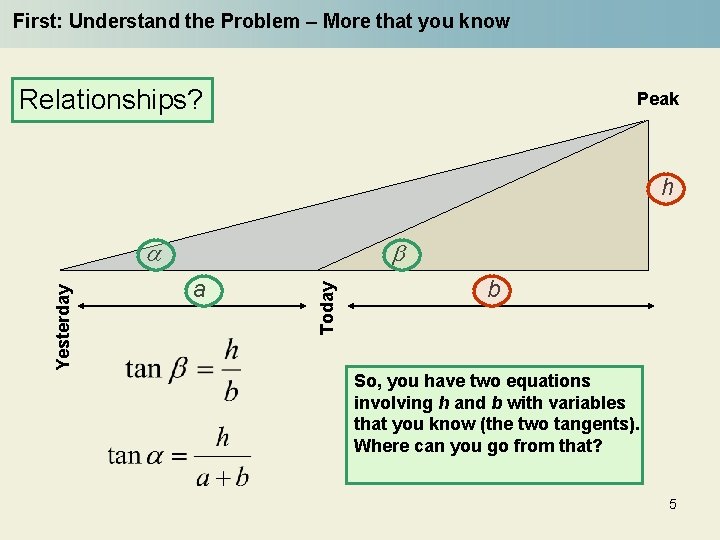
First: Understand the Problem – More that you know Relationships? Peak h b a Today Yesterday a b So, you have two equations involving h and b with variables that you know (the two tangents). Where can you go from that? 5

Second: Designing a Plan What can you get from the two tangents? What we seek! gets (1) gets (5) (2) Combining (1) and (2) gets (3) (6) Expanding (3) and then rearranging gets Now it’s plug and chug Then (4) So, solve (4) for b, and plug that into (1) 6

Third: Carrying out your Plan Do the Calculation Recreate this spreadsheet – If your spreadsheet returns a value of -2. 185, you used degrees instead of radians. Excel expects radians. For information about radians, click here So, here’s the answer: These measurements imply that the peak is about 34 mi away and about 8500 ft above you. 7

Fourth: Looking back The four steps we have been following are the four steps of Polya’s heuristic: 1. 2. 3. 4. Understanding the problem Designing a plan Carrying out the plan Looking back For information about George Polya: http: //www. sci. uidaho. edu/polya/biography. htm For more about Polya’s heurisitc: http: //www. math. utah. edu/~pa/math/polya. html Under looking back, we can ask if our answer is reasonable. Is it? If our elevation on the plain is 3500 ft above sea level, what is the elevation of the mountain? Are those numbers reasonable? Also under Looking Back Can we think of another way of solving the problem? Does the new way produce the same result? 8

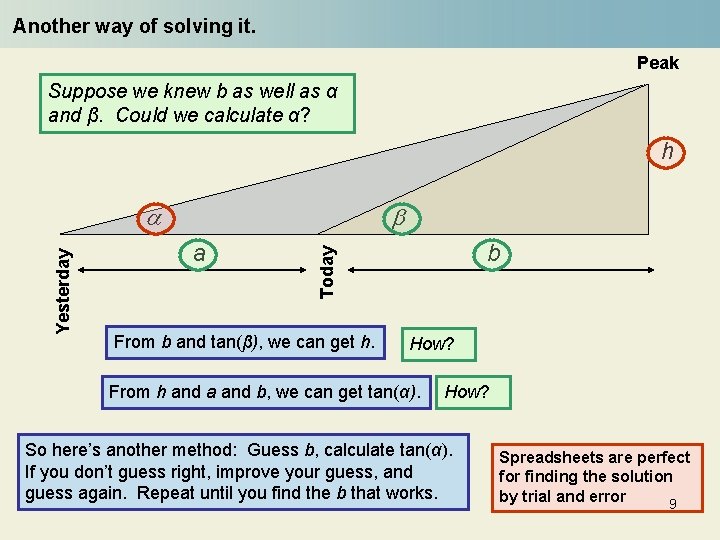
Another way of solving it. Peak Suppose we knew b as well as α and β. Could we calculate α? h b a b Today Yesterday a From b and tan(β), we can get h. How? From h and a and b, we can get tan(α). How? So here’s another method: Guess b, calculate tan(α). If you don’t guess right, improve your guess, and guess again. Repeat until you find the b that works. Spreadsheets are perfect for finding the solution by trial and error 9

Another calculation. Another spreadsheet. Recreate this spreadsheet – 50 miles is not a correct guess. Guess again, and again, until the two numbers agree. Or, you could try the value for b you got from the first method. 10

End of Module Assignment 1. It is now a day later. You are 12 miles closer to the peak. The angle of the line of sight to the peak is now 4. 15 above the horizontal. What are your new results for the distance to the mountain and its height above you? Hand in the new version of the spreadsheet of Slide 7. Check your answer by using the method of Slide 10 and hand in that spreadsheet too. 2. Using the spreadsheet of Slide 7, make yesterday’s angle 10% larger and today’s angle 10% smaller. What is the new height of the mountain above you? Is your new answer reasonable? How well do you measure angles when they are in the neighborhood of 2 degrees? Is 10% error a possibility? What do you think of the robustness (opposite of sensitivity) of the calculated height of the mountain with respect to errors in angle measurement? 3. Write a paragraph or two describing how Polya’s How to Solve It heuristic was applied in this module. 11

On radians • “Degree” as a measure of the size of an angle is arbitrary. There are 360 of them in a circle. Why not 100 or 1000? The answer has to do with history. • “Radian” is not arbitrary. Consider a pie slice. What is the angle of the slice? The outer rim of the crust is a circular arc. The arc length is the length of that circular arc. The length of the side of the piece of pie is the radius of the circle making (“subtending”) the circular arc. The ratio of the arc length to the radius is a measure of the size of the angle. It is a dimensionless quantity (length over length). The larger the piece of pie (meaning the larger the angle), the larger the arc length and hence the ratio of the arc length to radius. That ratio is the number of radians, an angular measure of the angle of that piece of pie. • From the definition of π, there are 2 π pi radians in a circle. Why? • Because there are 2 π radians in a circle, an equation relating radians to degrees is: π radians = 180 degrees. • Therefore, to convert degrees to radians: multiply by π/180. • And to convert radians to degrees: multiply by 180/ π. • So, the Excel equation for cos(20) is: =cos(20*pi()/180). • Excel uses pi() to call the value of pi. Alternatively, you can use 3. 14159. • Who defined radian? His brother had a lot to say about the age of the Earth and 12 is well known to geologists. See http: //www. unc. edu/~rowlett/units/dict. R. html Return to Slide 7.

El Capitan, Guadalupe Mountains Photo by Arthur Harris, UTEP http: //museum. utep. edu/archive/geology/DDgumo. htm http: //www. nps. gov/archive/gumo/adhi 1 a. htm The idea for this module came during a scenic drive from El Paso to Carlsbad, by El Capitan, a historic landmark for travelers, and the site of what is now the most famous Permian reef in the world. See: http: //en. wikipedia. org/wiki/Delaware_Basin, and http: //en. wikipedia. org/wiki/Guadalupe_Mountains_National_Park Return to Slide 2 13