Sistemas de ayuda a la decisin Modelizacin de

Sistemas de ayuda a la decisión Modelización de la incertidumbre Tema 2. Incertidumbre y Probabilidad Indice 1) Sucesos Aleatorios. 2) Espacio Muestral. 3) Operaciones con Sucesos. 4) Enfoques de la Probabilidad. 5) Axiomas de Kolmogorov. 6) Axiomas de la Probabilidad Subjetiva. 7) Resultados Básicos con Probabilidades. 8) Variables Aleatorias. 9) Educción de Probabilidades.

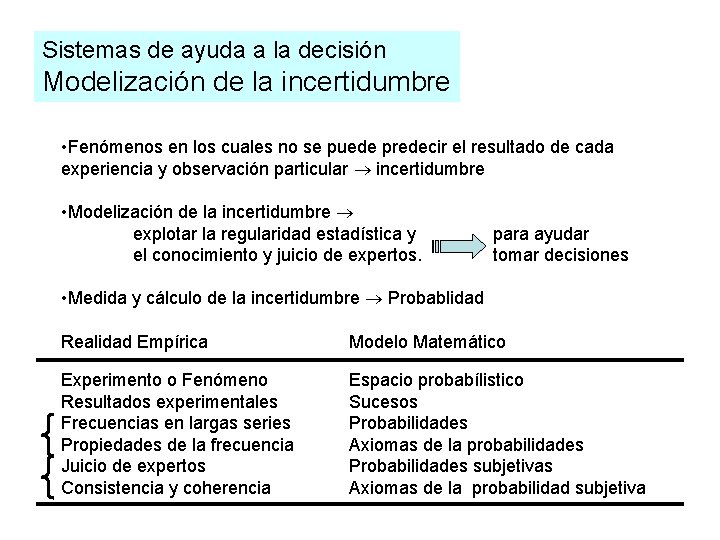
Sistemas de ayuda a la decisión Modelización de la incertidumbre • Fenómenos en los cuales no se puede predecir el resultado de cada experiencia y observación particular incertidumbre • Modelización de la incertidumbre explotar la regularidad estadística y el conocimiento y juicio de expertos. para ayudar tomar decisiones • Medida y cálculo de la incertidumbre Probablidad Realidad Empírica Modelo Matemático Experimento o Fenómeno Resultados experimentales Frecuencias en largas series Propiedades de la frecuencia Juicio de expertos Consistencia y coherencia Espacio probabílistico Sucesos Probabilidades Axiomas de la probabilidades Probabilidades subjetivas Axiomas de la probabilidad subjetiva

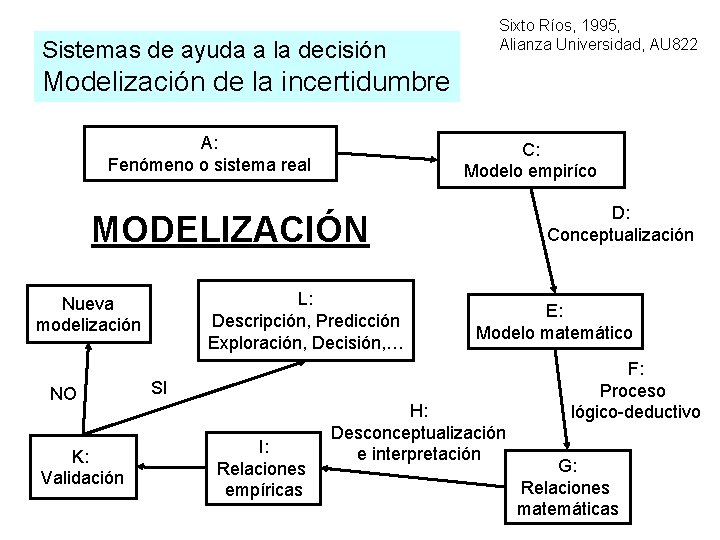
Sistemas de ayuda a la decisión Sixto Ríos, 1995, Alianza Universidad, AU 822 Modelización de la incertidumbre A: Fenómeno o sistema real C: Modelo empiríco D: Conceptualización MODELIZACIÓN L: Descripción, Predicción Exploración, Decisión, … Nueva modelización NO K: Validación E: Modelo matemático SI I: Relaciones empíricas H: Desconceptualización e interpretación F: Proceso lógico-deductivo G: Relaciones matemáticas

Modelización de la incertidumbre Sucesos aleatorios. Espacio muestral • Experimentos y Fenómenos Deterministas: {Condiciones} Resultado; Aleatorios: {Condiciones} {Resultados} • Experimento y Fenómeno Aleatorio: un conjunto de reglas y condiciones de realización; es repetible y el resultado manifiesta azar • Sucesos Elementales: resultados exhaustivos y excluyentes que observamos en las realizaciones del experimento y descritos mediante proposiciones simples • Sucesos Aleatorios: posibles resultados observados en un experimento aleatorio y descritos mediante proposiones simples, compuestas y/o predicados • Espacio Muestral: conjunto de los sucesos elementales, E • Espacio de Sucesos: conjunto de todos los sucesos aleatorios; conjunto de los subconjuntos del espacio muestral, (E), |E|=n, | (E)| = 2 n

Modelización de la incertidumbre Sucesos aleatorios. Espacio muestral • Tras un experimento aleatorio siempre observamos un suceso-resultado de E • El conjunto E debe ser exhaustivo contemplando todas las posibilidades lógicas, con independencia de que a priori se puedan calificar ciertos resultados de excepcionales frente a otros que se consideran normales • Tras un experimento aleatorio ocurre el suceso A si el resultado elemental observado es un elemento de A • En un experimento aleatorio decimos que el suceso A está incluido en el suceso B, A B, si la observación de A ímplica la observación de B • Dos sucesos son iguales si A B y B A • ( (E), ) es un conjunto parcialmente ordenado • es minimal, E es maximal y los sucesos elementales junto a son los átomos

Modelización de la incertidumbre Operaciones con sucesos • Sucesos disjuntos o incompatibles en un experimento aleatorio cuando no se observan simultaneamente, la observación de uno excluye al resto • Intersección de sucesos : (E), (A, B) A B Se observa el suceso intersección si se observan ambos • Unión de sucesos : (E), (A, B) A B Se observa el suceso unión si se observa al menos uno • Suceso complementario o contrario de A es el suceso observado cuando no observamos A. Se denota con ¬A. ¬E = , E = ¬ , A ¬A = E, A ¬A = , A B ¬A • Sucesos Seguro e Imposible: el espacio muestral, E, se observa seguro; el suceso que nunca se observa es ¬E, es imposible, y se simboliza con • Diferencia de sucesos: A – B = A ¬B, observamos A y ¬B • Diferencia simétrica de sucesos: A B = (A – B) (B – A)

Modelización de la incertidumbre Operaciones con sucesos • Álgebra de Boole de sucesos. E y (E), con las operaciones , , ¬, A, B, C (E) 1. Conmutativas: A B = B A, A B = B A 2. Asociativas: A (B C) = (A B) C, A (B C) = (A B) C 3. elemento neutro: A = A, A E = A 4. Distributivas: A (B C) = (A B) (A C), A (B C) = (A B) (A C) 5. Complementario: A ¬A = E, A ¬A = ( (E), , , ¬) es un Álgebra de Boole • Propiedades: 6. Idempotencia: A A = A, A A = A 7. Maximalidad-minimalidad: A E = E, A = 8. Involución: ¬(¬A)) = A 9. Simplificación o absorción: A (A B) = A, A (A B) = A 10. Leyes de Morgan: ¬(A B) = ¬A ¬B, ¬(A B) = ¬A ¬B • Definiciones alternativas: Axiomática de Huntington (props. {1, 3, 4 y 5}) y Retículo distributivo y complementario (props. {1, 2, 6, y 9} (retículo) y {4 y 5}) Principio de Dualidad ( , E )

Modelización de la incertidumbre Enfoques de la Probabilidad Enfoque Clásico Laplace, “Teoría analítica de probabilidades” 1812 Supuesto que todos los resultados elementales son igualmente verosímiles, la probabilidad de un suceso es el cociente entre el número de resultados favorables y el número total de resultados posibles Probabilidad de A = cardinal de A / cardinal de E = |A| / |E| • Hipótesis de simetría respecto al espacio muestral que puede no ser cierta en muchos experimentos aleatorios • Si el número de total de resultados no es finito no se puede calcular el cociente

Modelización de la incertidumbre Enfoques de la Probabilidad Enfoque Frecuentista (Richard Von Mises (1883 -1953) ) Experimento aleatorio repetido N veces Espacio muestral E y un suceso A que se observa n veces, 0 n N Frecuencia Absoluta de A: n Frecuencia Relativa de A: f(A) = n/N Propiedades de la frecuencia relativa (A y B (E)): 1. 0 f(A) 1 2. f(¬A) = 1 – f(A) 3. A B f(A) < f(B) 4. A B = f(A B) = f(A) + f(B) 5. f(E) = 1 6. f(A B) = f(A) + f(B) – f(A B) • Contexto de un experimento aleatorio que se repite indefinidamente en identicas condiciones. Probabilidad como límite empírico: Probabilidad de A = límite n/N, n • Conflicto: condiciones estables en un tiempo indefinido

Modelización de la incertidumbre Enfoques de la Probabilidad Enfoque Subjetivo o Personal (Finetti, 1975; French, 1986) Contexto de un suceso que puede observarse una sola vez La probabilidad representa el grado de creencia de que se observe un suceso o que el sistema presente un cierto estado Probabilidad de A = cuantificación de la creencia en la observación de A tras la observación de cierta Información relevante o evidencia • Enfoque natural para la representación y el análisis de juicios con imprecision • Enfoque personal, las probabilidades se asocian al observador no al sistema objeto • La probabilidad está definida por el grado de creencia personal y el grado de información disponible, que puede cambiar y actualizar la probabilidad • La cuantificación del grado de creencia es un probabilidad si verifica la Axiomática de Kolmogorov u otra axiomatización que garantice la coherencia

Modelización de la incertidumbre Axiomas de Kolmogorov Axiomas de la Teoría de la Probabilidad (Kolmogorov, 1933) Se basa en la Teoría de la Medida Fundamenta el concepto de probabilidad y el cálculo de probabilidades • Definición de -Álgebra A: 1. A A ¬ A A 2. {Ai} i=1 A i=1 Ai A , y ¬ son leyes de composición interna en la -Álgebra. Ej’s: (E) y {E, } • Espacio Probabilizable: (E, A) • Probabilidad en (E, A) es toda aplicación P: A +, que verifique los axiomas: A 1. P(E) = 1 A 2. {Ai} i=1 A, Ai Aj = , i j P( i=1 Ai ) = i=1 P(Ai) • Espacio de Probabilidad: (E, A, P). E finito, infinito numerable, continuo. • Propiedades de una probabilidad. A y B sucesos de un (E, A, P) 1. P( ) = 0 2. P(¬A) = 1 – P(A) 3. A B P(A) P(B) 4. 0 P(A) 1 5. P(A B) = P(A) + P(B) – P(A B)

Modelización de la incertidumbre Axiomas de la Probabilidad Subjetiva A, B y C (E, A, P. Subjetiva) El decisor/experto tiene percepción inherente de verosimilitud relativa y puede decir: A más verosímil que B, menos o igual. Relación binaria A B: “A al menos tan verosímil como B” • S 1. es un orden débil (transitividad, completud, consistencia) • S 2. Independencia de sucesos comunes: si A C = B C = A B A C • S 3. No trivialidad: A B C p , A 1 -p • S 4. El experimento de referencia, donde el decisor/experto está preparado para considerar sus creencia (rueda de la fortuna) • S 5. Continuidad: A, el decisor/experto puede identificarlo con un suceso sobre la rueda de la fortuna à tal que A ~ à • S 6. Equivalencia de certidumbres: ( ) = 360º

Modelización de la incertidumbre Axiomas de la Probabilidad Subjetiva Si se verifican los 6 axiomas existe una única medida de probabilidad que satisface "probabilidades mayores a sucesos más verosímiles" Los axiomas S 1 -S 6 garantizan que ! P tal que A B P(A) P(B) • Construcción P() = (A) / 360º • Verifica los axiomas A 1 y A 2 de Kolmogorov • French muy basado en De. Groot (1979) • Otros sistemas axiomáticos: DE Finetti (1937), Raiffa (1968), Ramsey (1931), Savage (1954)

Modelización de la incertidumbre Resultados Básicos con Probabilidades A, B y C (E, A, P) • Probabilidad de la unión: P(A B) = P(A)+P(B)-P(A B) P(A B C) = P(A)+P(B)+P(C)-P(A B)-P(A C)-P(B C)+P(A B C) • Probabilidades conjuntas: P(A B), P(A ¬B), P(¬A ¬B) 22 sucesos Incompatibles. Tabla de doble entrada, dos dimensiones. P(A B C), P(A B ¬C), P(A ¬B ¬C) P(¬A B C), P(¬A B ¬C), P(¬A ¬B ¬C). 23 sucesos Incompatibles. Tabla de triple entrada, tres dimensiones. • Probabilidades marginales (sucesos incompatibles, suma por dimensiones): P(A) = P(A B C)+P(A B ¬C)+P(A ¬B ¬C) P(A) = P(A B C A B ¬C)+P(A ¬B C A ¬B ¬C) P(A) = P(A B (C ¬C)) + P(A ¬B (C ¬C)) P(A) = P(A B E)+P(A ¬B E) = P(A B A ¬B ) = P(A E) = P(A)

Modelización de la incertidumbre Resultados Básicos con Probabilidades • Probabilidades condicionadas: P( A | B) = P(A B) / P(B), P( B | A) = P(A B) / P(A), P(A | B C) = P(A B C) / P(B C), …. (E, A, P(. |B)) espacio de probabilidad condicionado a B (E), P(B) > 0. • Probabilidad de la intersección Regla de multiplicación o Tma de producto P(A B) = P(A | B) P(B) = P(B| A) P(A B C) = P(A) P(B | A) P(C | A B) = P(B) P(A | B) P(C | A B), …. • Independencia e independencia mutua. P( A | B) = P(A), P( B | A) = P(B), P(A B) = P(A) P(B) P(A B C) = P(A) P(B) P(C), P(A B) = P(A) P(B), P(A C) = P(A) P(C), P(B C) = P(B) P(C), en general, 2 n-1 condiciones necesarias y suficientes para la independencia de n sucesos. • Teorema de la Probabilidad Total 1. A 1, . . An, n sucesos tales que Ai Aj = , i j, i=1 Ai = E y se conocen P(Ai), 2. B (E), tal que se conocen (B | Ai) P(B) = P(B E) = P( B ( i=1 Ai )) = i=1 P(B | Ai) P(Ai) {Ai} i=1 A: partición o sistema completo de sucesos

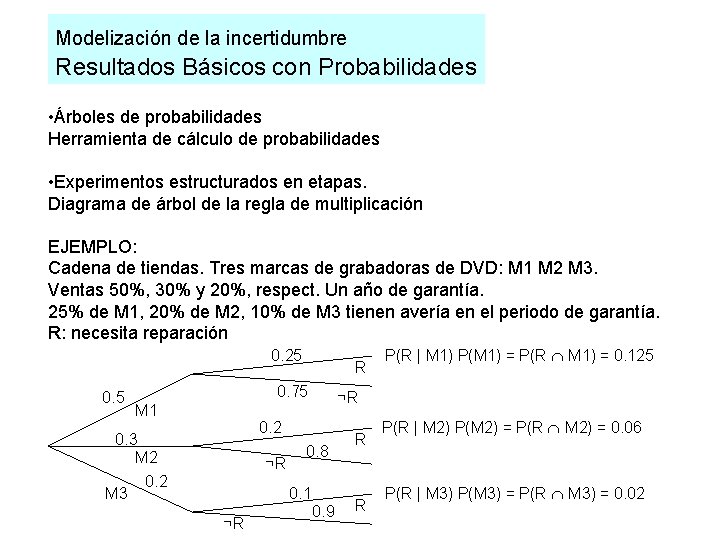
Modelización de la incertidumbre Resultados Básicos con Probabilidades • Árboles de probabilidades Herramienta de cálculo de probabilidades • Experimentos estructurados en etapas. Diagrama de árbol de la regla de multiplicación EJEMPLO: Cadena de tiendas. Tres marcas de grabadoras de DVD: M 1 M 2 M 3. Ventas 50%, 30% y 20%, respect. Un año de garantía. 25% de M 1, 20% de M 2, 10% de M 3 tienen avería en el periodo de garantía. R: necesita reparación 0. 25 0. 75 M 1 ¬R 0. 2 0. 8 0. 1 ¬R P(R | M 1) P(M 1) = P(R M 1) = 0. 125 ¬R 0. 2 0. 3 M 2 M 3 R 0. 9 R R P(R | M 2) P(M 2) = P(R M 2) = 0. 06 P(R | M 3) P(M 3) = P(R M 3) = 0. 02

Modelización de la incertidumbre Resultados Básicos con Probabilidades Revisión de juicios y teorema de Bayes. Interpretación de pruebas diagnósticas y toma de decisiones. • Observaciones Juicio Inicial 1. Hipótesis: Probabilidades a priori 2. Conocimiento Experto, Protocolo SRI, Heurísticas y Sesgos, Imprecisión 3. Nuevos datos y resultados revisión de las Hipótesis: a posteriori • Precisión de los resultados de una prueba o test. Tabla de contingencia. Causa Pre Aus R: resultados totales Test Pos VP FP R = VP+FN+FP+VN Neg FN VN Marginales: P(Causa=Presente) = (VP+FN)/R, P(Test=Pos) = (VP+FP)/R • Rendimiento del Test - Medidas de Concordancia | Discordancia, tasas: Sensibilidad Especificidad TVP = VP / (VP+FN) TVN = VN / (FP+VN) TFP = FP / (VN+FP) = 1 -TVN TFN = FN / (VP+FN) = 1 -TVP

Modelización de la incertidumbre Resultados Básicos con Probabilidades Ejemplo clínico: Test de tolerancia a esfuerzo, criterio de resultado +: caida 1 mm del segmento TS (electrocardiograma) punto de decisión Test Enferm Pos Neg total Pre 840 210 1050 Aus 117 333 450 total 957 543 1500 • Sensibilidad TVP = 80%, Especificidad TVN = 74%, TFN = 20%, TFP = 26% • Si cambia el criterio cambia TVP y TVN. 2 mm TVP , TVN , es más estricto • El rendimiento del test depende del punto de decisión, que depende del problema, objetivos del test y tratamientos. enfermedad rara: alta especifidad, enfermedad grave + terapia segura: mínimo de falsos negativos enfermedad leve + terapia de riesgo: mínimo de falsos positivos

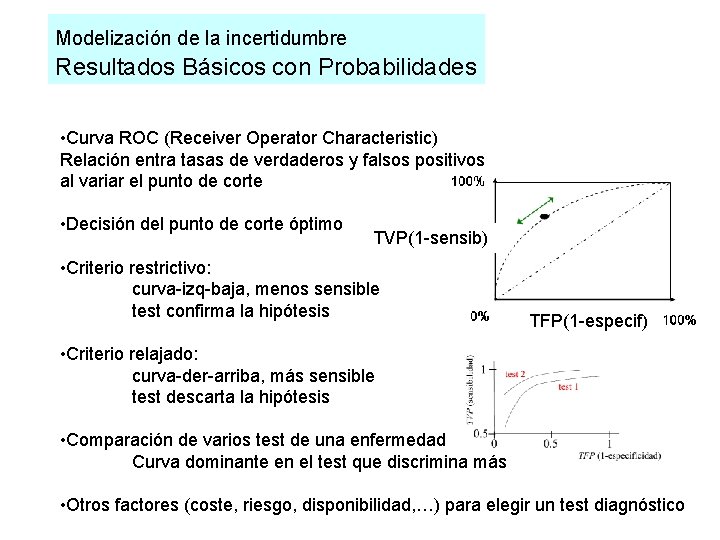
Modelización de la incertidumbre Resultados Básicos con Probabilidades • Curva ROC (Receiver Operator Characteristic) Relación entra tasas de verdaderos y falsos positivos al variar el punto de corte • Decisión del punto de corte óptimo TVP(1 -sensib) • Criterio restrictivo: curva-izq-baja, menos sensible test confirma la hipótesis TFP(1 -especif) • Criterio relajado: curva-der-arriba, más sensible test descarta la hipótesis • Comparación de varios test de una enfermedad Curva dominante en el test que discrimina más • Otros factores (coste, riesgo, disponibilidad, …) para elegir un test diagnóstico

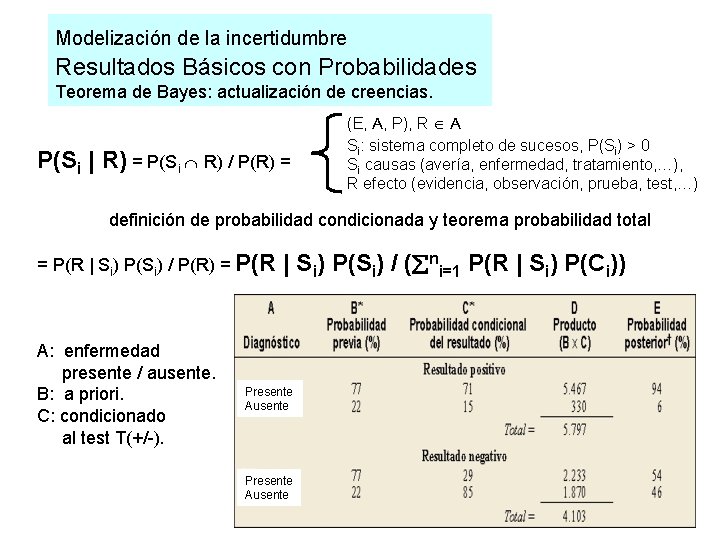
Modelización de la incertidumbre Resultados Básicos con Probabilidades Teorema de Bayes: actualización de creencias. P(Si | R) = P(Si R) / P(R) = (E, A, P), R A Si: sistema completo de sucesos, P(Si) > 0 Si causas (avería, enfermedad, tratamiento, …), R efecto (evidencia, observación, prueba, test, …) definición de probabilidad condicionada y teorema probabilidad total = P(R | Si) P(Si) / P(R) = P(R A: enfermedad presente / ausente. B: a priori. C: condicionado al test T(+/-). | Si) P(Si) / ( ni=1 P(R | Si) P(Ci)) Presente Ausente

Modelización de la incertidumbre Resultados Básicos con Probabilidades Teorema de Bayes: actualización de creencias. P(A) = 0. 77, P(T+| A) = 0. 71, P(T-| A) = 0. 29, P(¬A) = 0. 22 P(T+| ¬A) = 0. 15 P(T-| ¬A) = 0. 85 A: enfermedad (presente / ausente). Test T(+/-). P(T+) = (P(T+| A) P(A)+P(T+| ¬A) P(¬A)) = 0. 579. P(T-) = (P(T-| A) P(A)+P(T-| ¬A) P(¬A)) = 0. 410. P(T+)+P(T-)=1. 0. P(A| T+) = P(T+| A) P(A) / P(T+) = 0. 71*0. 77 / (0. 71*0. 77+0. 15*0. 22) = 0. 943 P(¬A| T+) = P(T+| ¬A) P(¬A) / P(T+) = 0. 15*0. 22 / (0. 71*0. 77+0. 15*0. 22) = 0. 056 P(A|T+)+P(¬A|T+)=1. 0. P(A| T-) = P(T-| A) P(A) / P(T-) = 0. 29*0. 77 / (0. 29*0. 77+0. 85*0. 22) = 0. 544 P(¬A| T-) = P(T-| ¬A) P(¬A) / P(T-) = 0. 85*0. 22 / (0. 29*0. 77+0. 85*0. 22) = 0. 455 P(A|T-)+P(¬A|T-)=1. 0. Interpretación