Shengyu Zhang The Chinese University of Hong Kong

Shengyu Zhang The Chinese University of Hong Kong

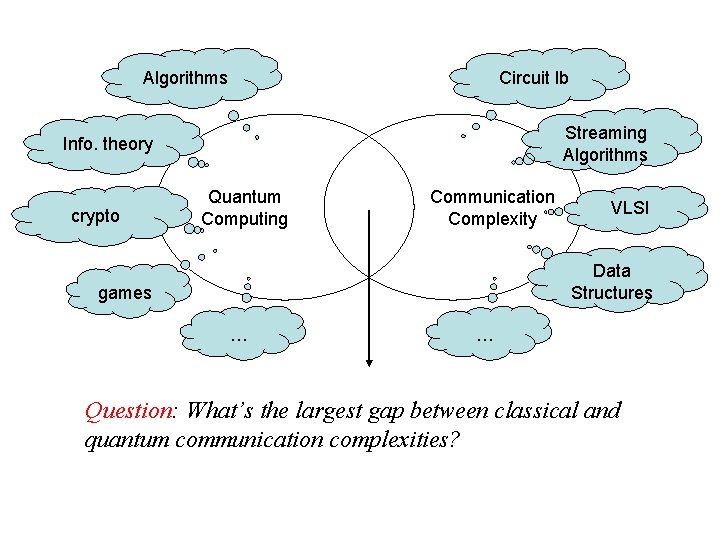
Algorithms Circuit lb Streaming Algorithms Info. theory crypto Quantum Computing Communication Complexity VLSI Data Structures games … … Question: What’s the largest gap between classical and quantum communication complexities?

Communication complexity • [Yao 79] Two parties, Alice and Bob, jointly compute a function f(x, y) with x known only to Alice and y only to Bob. x y Alice Bob f(x, y) • Communication complexity: how many bits are needed to be exchanged?

Various protocols • Deterministic: D(f) • Randomized: R(f) – A bounded error probability is allowed. – Private or public coins? Differ by ±O(log n). • Quantum: Q(f) – A bounded error probability is allowed. – Assumption: No shared Entanglement. (Does it help? Open. )

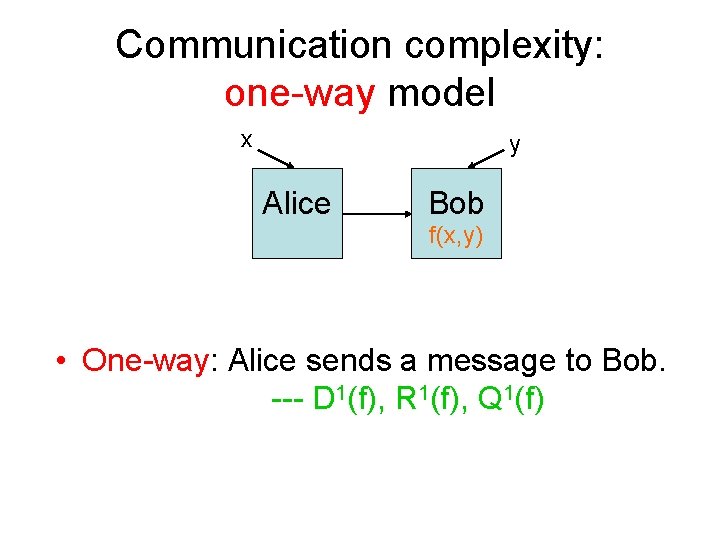
Communication complexity: one-way model x y Alice Bob f(x, y) • One-way: Alice sends a message to Bob. --- D 1(f), R 1(f), Q 1(f)

About one-way model • Power: As efficient as the best two-way protocol. – Efficient protocols for specific functions such as Equality, Hamming Distance, and in general, all symmetric XOR functions. • Applications: – Lower bound for space complexity of streaming algorithms. • Lower bound? Can be quite hard, especially for quantum.

Question • Question: What’s the largest gap between classical and quantum communication complexities? • Partial functions, relations: exponential. • Total functions, two-way: – Largest gap: Q(Disj) = Θ(√n), R(Disj) = Θ(n). – Best bound: R(f) = exp(Q(f)). • Conjecture: R(f) = poly(Q(f)).

Question • Question: What’s the largest gap between classical and quantum communication complexities? • Partial functions, relations: exponential. • Total functions, one-way: – Largest gap: R 1(EQ) = 2∙Q 1(EQ), – Best bound: R 1(f) = exp(Q 1(f)). • Conjecture: R 1(f) = poly(Q 1(f)), – or even R 1(f) = O(Q 1(f)).

Approaches • Approach 1: Directly simulate a quantum protocol by classical one. – [Aaronson] R 1(f) = O(m∙Q 1(f)). • Approach 2: L(f) ≤ Q 1(f) ≤ R 1(f) ≤ poly(L(f)). – [Nayak 99; Jain, Z. ’ 09] R 1(f) = O(Iμ∙VC(f)), where Iμ is the mutual info of any hard distribution μ. • Note: For the approach 2 to be possibly succeed, the quantum lower bound L(f) has to be polynomially tight for Q 1(f).

Main result • There are three lower bound techniques known for Q 1(f). – Nayak’ 99: Partition Tree – Aaronson’ 05: Trace Distance – The two-way complexity Q(f) • [Thm] All of these lower bounds can be arbitrarily weak. • Actually, random functions have Q(f) = Ω(n), but the first two lower bounds only give O(1).

Next • Closer look at the Partition Tree bound. • Compare Q and Partition Tree (PT) and Trace Distance (TD) bounds.

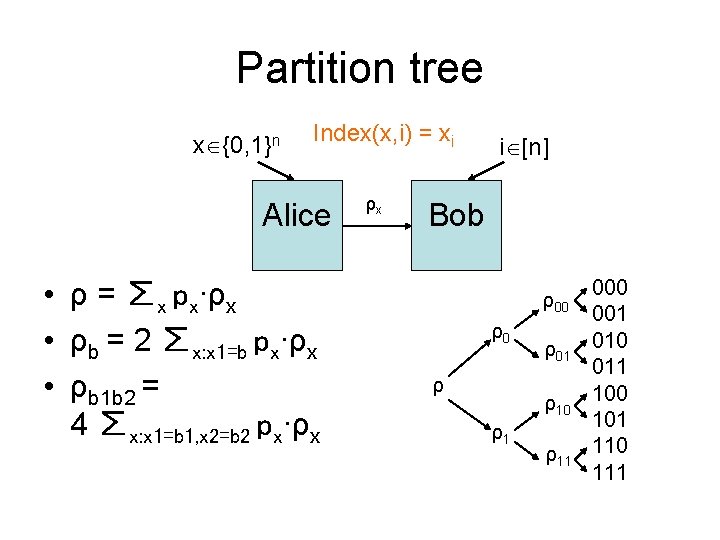
Nayak’s info. theo. argument x {0, 1}n Index(x, i) = xi Alice ρx i [n] Bob • [Nayak’ 99] Q 1(Index) = Ω(n). – ρx contains Ω(1) info of x 1, since i may be 1. – Regardless of x 1, ρx contains Ω(1) info of x 2. – And so on.

Nayak’s info. theo. argument x {0, 1}n Index(x, i) = xi Alice ρx i [n] Bob • ρ = ∑x px∙ρx • S(ρ) = S(½ρ0+½ρ1) // ρb = 2 ∑x: x_1=b px∙ρx ≥ I(X 1, M 1) + ½S(ρ0)+½S(ρ1) // Holevo bound. M 1: Bob’s conclusion about X 1 ≥ 1 – H(ε) + ½S(ρ0)+½S(ρ1) // Fano’s Inequ. ≥ … ≥ n(1 – H(ε)).

Partition tree x {0, 1}n Index(x, i) = xi Alice • ρ = ∑x px∙ρx • ρb = 2 ∑x: x 1=b px∙ρx • ρb 1 b 2 = 4 ∑x: x 1=b 1, x 2=b 2 px∙ρx ρx i [n] Bob ρ00 ρ0 ρ ρ01 ρ10 ρ1 ρ11 000 001 010 011 100 101 110 111

Partition tree x {0, 1}n Index(x, i) = xi Alice ρx • ρ = ∑x px∙ρx • In general: – Distri. p on {0, 1}n – Partition tree for {0, 1}n – Gain H(δ)-H(ε) at v • v is partitioned by (δ, 1 -δ) i [n] Bob 0 0 0 1 1 1 0 0 1 1

Issue • [Fano’s inequality] I(X; Y) ≥ H(X) – H(ε). – X, Y over {0, 1}. – ε = Pr[X ≠ Y]. H(δ) • What if H(δ) < H(ε)? • Idea 1: use success amplification to decrease ε to ε*. • Idea 2: give up those vertices v with small H(X). • Bound: max. T, p, ε* log(1/ε*)∙∑vp(v)[H(Xv)-H(ε*)]+ • Question: How to calculate this?

Picture clear • max. T, p, ε* log(1/ε*)∙∑vp(v)[H(Xv)-H(ε*)]+ • Very complicated. Compare to Index where the tree is completely binary and each H(δv) = 1 (i. e. δv=1/2). • [Thm] the maximization is achieved by a complete binary tree with δv=1/2 everywhere.

Two interesting comparisons • Comparison to decision tree: – Decision tree complexity: make the longest path short – Here: make the shortest path long. • Comparison to VC-dim lower bound: [Thm] The value is exactly the extensive equivalence query complexity. – A measure in learning theory. – Strengthen the VC-dim lower bound by Nayak.

Trace distance bound • [Aaronson’ 05] – μ is a distri on 1 -inputs – D 1: (x, y) ← μ. – D 2: y ← μ, x 1, x 2 ← μy. Then Q 1(f) = Ω(log ∥D 2 -D 12∥ 1 -1)

Separation • [Thm] Take a random graph G(N, p) with ω(log 4 N/N) ≤ p ≤ 1 -Ω(1). Its adjacency matrix, as a bi-variate function f, has the following w. p. 1 -o(1) Q(f) = Ω(log(p. N)). • Q*(f) ≥ Q(f) = Ω(log(1/disc(f))). • disc(f) is related to σ2(D-1/2 AD-1/2), which can be bounded by O(1/√p. N) for a random graph.

• [Thm] For p = N-Ω(1), PT(f) = O(1) w. h. p. – By our characterization, it’s enough to consider complete binary tree. – For p = N-Ω(1), each layer of tree shrinks the #1’s by a factor of p. • p. N → p 2 N → p 3 N → … → 0: Only O(1) steps. • [Thm] For p = o(N-6/7), TD(f) = O(1) w. h. p. – Quite technical, omitted here.

Putting together • [Thm] Take a random graph G(N, p) with ω(log 4 N/N) ≤ p ≤ 1 -Ω(1). Its adjacency matrix, as a bi-variate function f, has the following w. p. 1 -o(1) Q(f) = Ω(log(p. N)). • [Thm] For p = o(N-6/7), TD(f) = O(1) w. h. p. • [Thm] For p = N-Ω(1), PT(f) = O(1) w. h. p. • Taking p between ω(log 4 N/N) and o(N-6/7) gives the separation.

Discussions • Negative results on the tightness of known quantum lower bound methods. • Calls for new method. • Somehow combine the advantages of these methods? – Hope the paper shed some light on this by identifying their weakness.