Security Markets IX Miloslav S Vosvrda Theory of







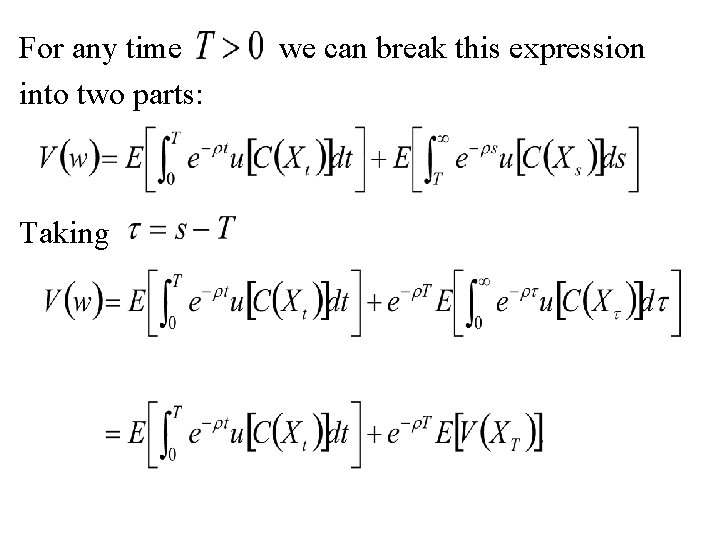


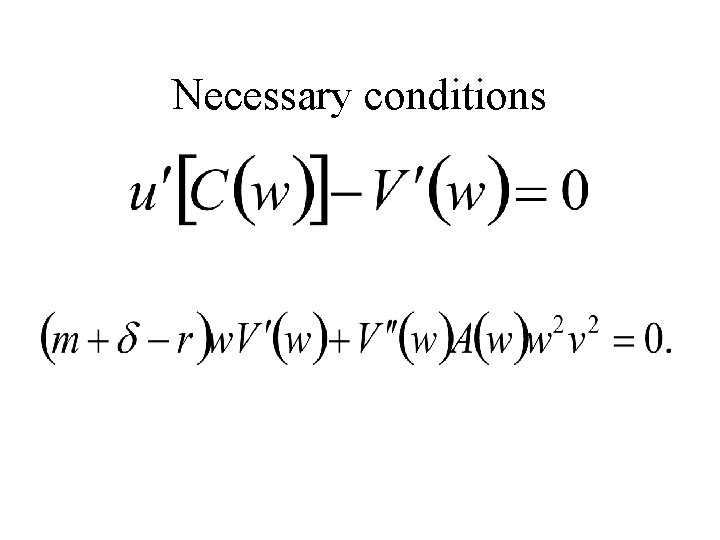
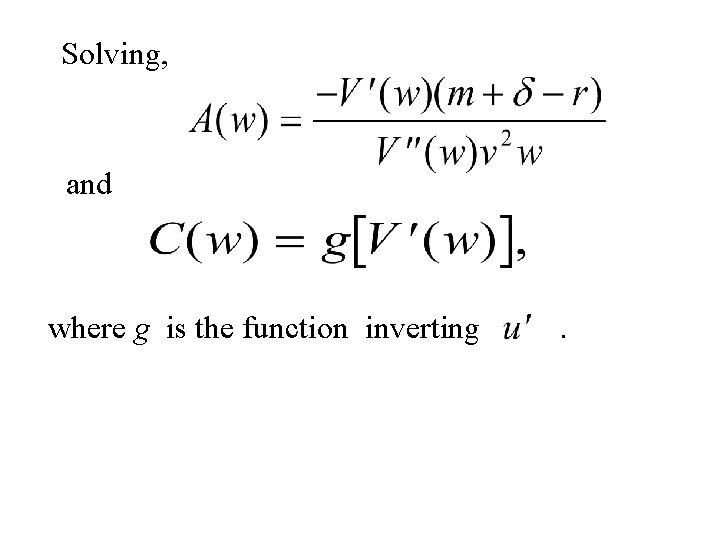



- Slides: 15

Security Markets IX Miloslav S. Vosvrda Theory of Capital Markets

Portfolio Control Problem We apply Ito‘s Lemma to the following portfolio control problem. We assume that a risky security has a price process S satisfying the stochastic differential equation and pays dividends at the rate of at any time t, where m, v and are strictly positive scalars. We may think heuristically of as the „instantaneous expected rate of return„ and as the „instantaneous variance of the rate of return“.

A riskless security has a price that is always one, and pays dividends at the constant interest rate r, where. Let denote the stochastic process for the wealth of an agent who may invest in the two given securities and withdraw funds for consumption at the rate at any time.

If is the fraction of total wealth invested at time t in the risky security, it follows that X satisfies the stochastic differential equation: which should be easily enough interpreted. Simplifying, We assume that wealth constraint is

We suppose that our investor derives utility from a consumption process according to where is a discount factor, and u is a strictly increasing, differentiable, and strictly concave function. The problem of optimal choice of portfolio and consumption rate is solved as follows. Of course, and can only depend on the information available at time t.

Because the wealth constitutes all relevant information at any time t, we may limit ourselves without loss of generality to the case and for some (measurable) functions A and C. We suppose that A and C are optimal, and note that where and w>0 is the given initial wealth.

Indirect utility The indirect utility for wealth w is
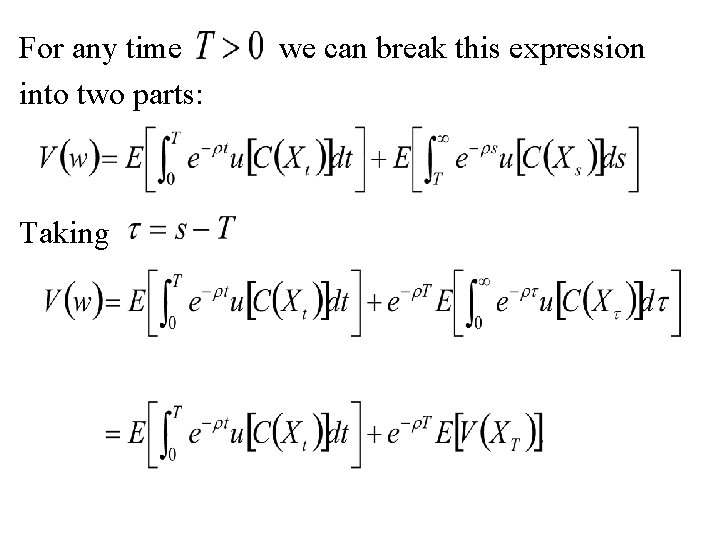
For any time into two parts: Taking we can break this expression

Adding and subtracting We divide each term by T and take limits as T converges to 0, using Ito‘s Lemma and l‘Hopital‘s Rule to arrive at where

A and C are optimal If A and C are indeed optimal, that is, if they maximize , then they must maximize for any time T. This is equivalent to the problem:
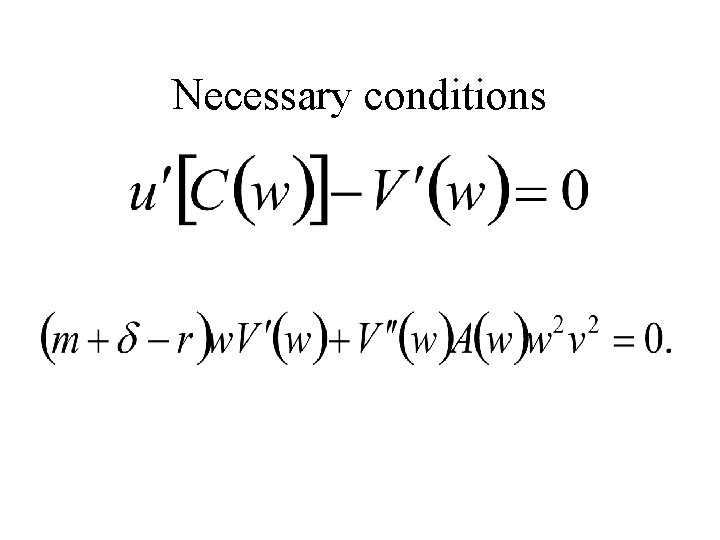
Necessary conditions
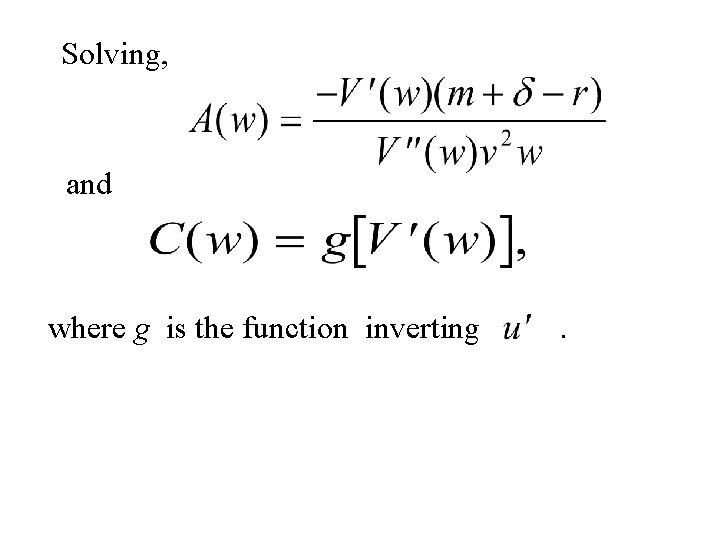
Solving, and where g is the function inverting .

An example If for some scalar risk aversion coefficient then. Substituing C and A from these expressions into leaves a second order differential equation for V that has a general solution. It follows that and where

In other words, it is optimal to consume at a rate given by a fixed fraction of wealth and to hold a fixed fraction of wealth in the risky asset. It is a key fact that the objective function is quadratic in A(w).

Consumption-Based Capital Asset Pricing Model This property carries over to a general constinuoustime setting. As the Consumption-Based Capital Asset Pricing Model (CCAPM) holds for quadratic utility functions, we should not then be overly surprised to learn that a version of the CCAPM applies in continuous-time, even for agents whose preferences are not strictly variance averse.
 Miloslav fialka
Miloslav fialka Michal miloslav hodža
Michal miloslav hodža Privat security
Privat security How would you define efficient security markets
How would you define efficient security markets From efficient markets theory to behavioral finance
From efficient markets theory to behavioral finance Efficient market hypothesis
Efficient market hypothesis What is the osi security architecture?
What is the osi security architecture? Security guide to network security fundamentals
Security guide to network security fundamentals Wireless security in cryptography
Wireless security in cryptography Visa international security model diagram
Visa international security model diagram Electronic mail security in network security
Electronic mail security in network security Cnss model 27 cells example
Cnss model 27 cells example E commerce security meaning
E commerce security meaning Software security building security in
Software security building security in Security guide to network security fundamentals
Security guide to network security fundamentals Security guide to network security fundamentals
Security guide to network security fundamentals





























