Rolling And Extrusion ME 482 Manufacturing Systems Rolling













- Slides: 17

Rolling And Extrusion ME 482 - Manufacturing Systems

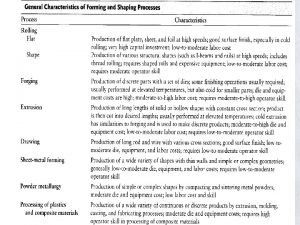
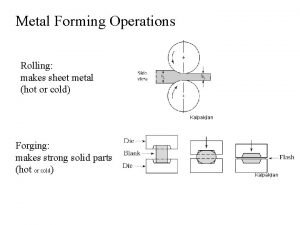
Rolling Process Points: • Significant shape change • Capital intensive • Large volume • Usually hot worked (isotropic)* • Oxide scale • Tolerances difficult to hold * Can be followed by cold rolling to improve tolerances and directional properties ME 482 - Manufacturing Systems

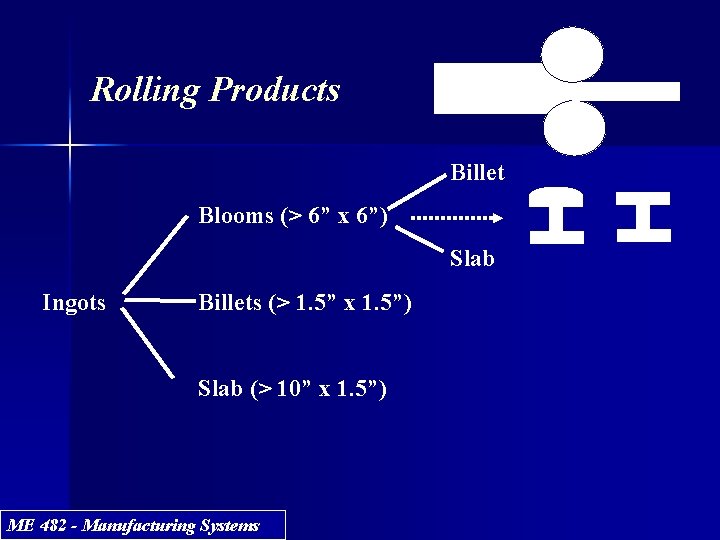
Rolling Products Billet Blooms (> 6” x 6”) Slab Ingots Billets (> 1. 5” x 1. 5”) Slab (> 10” x 1. 5”) ME 482 - Manufacturing Systems

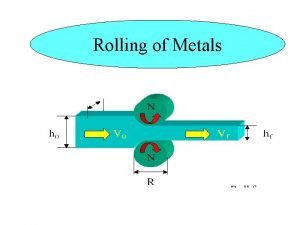
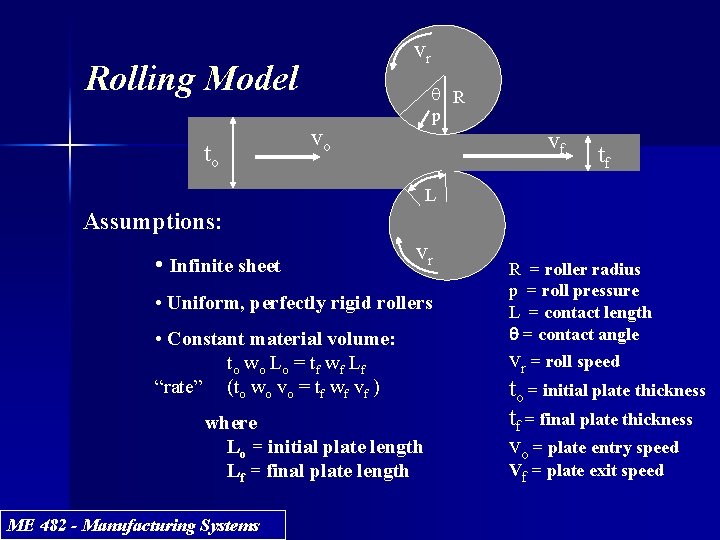
vr Rolling Model to q R p vo vf tf L Assumptions: • Infinite sheet vr • Uniform, perfectly rigid rollers • Constant material volume: t o wo L o = t f wf L f “rate” (to wo vo = tf wf vf ) where Lo = initial plate length Lf = final plate length ME 482 - Manufacturing Systems R = roller radius p = roll pressure L = contact length q = contact angle vr = roll speed to = initial plate thickness tf = final plate thickness vo = plate entry speed Vf = plate exit speed

Rolling Model Define draft = d = to - tf Draft limit = dmax = m 2 R m = 0. 1 cold m = 0. 2 warm m = 0. 4 – 1. 0 hot Define forward slip = s = (vf – vr)/vr Does it make sense that vr < vf? ME 482 - Manufacturing Systems Point of greatest contact pressure = no slip point

Rolling Model – stress, strain, force, power Define true strain = e = ln(to/tf) (Note: use to/tf to keep > 0) Apply average flow stress = Yf = K en /(1 + n) Approximate roll force = F = Yf w L where L = R(to – tf) R Torque estimated by T = 0. 5 F L Power = P = Tw = 2 p w F L (for two rollers) ME 482 - Manufacturing Systems q L R– (to–tf)/2

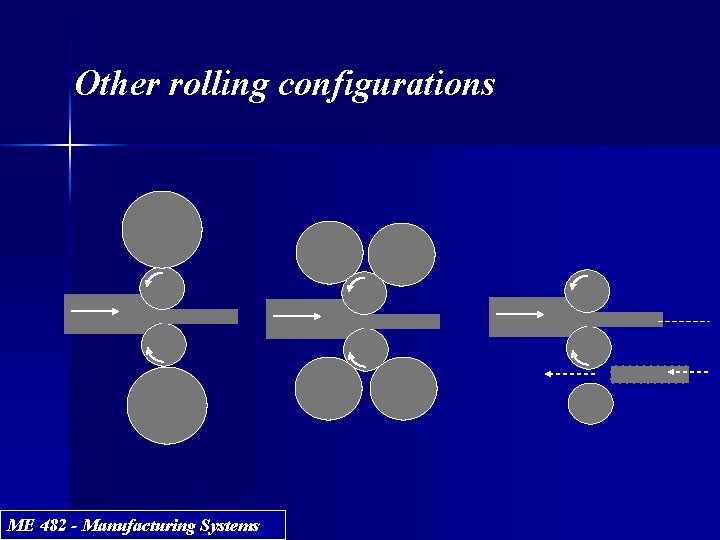
Other rolling configurations ME 482 - Manufacturing Systems

Example 21. 1 in text Roll a 12 inch wide strip, that is 1 inch thick, to 0. 875 inch thickness in one pass with roll speed of 50 rpm and radius = 10 inches. Material has K = 40, 000 psi, n = 0. 15 and m = 0. 12. Determine if feasible and calculate F, T, and power if so. Solution: Feasible since dmax = (0. 12)2 (10) = 0. 144 in. > d = 1. 0 – 0. 875 = 0. 125 in. Contact length = L = 1. 118 in. e = ln(1. 0/0. 875) = 0. 134 Yf = (40, 000)(0. 134)0. 15/1. 15 = 25, 729 psi Rolling force = (25, 729)(12)(1. 118) = 345, 184 lb Torque = (0. 5)(345, 184)(1. 118) = 192, 958 in. -lb Power = P = (2 p)(50)(345, 184)(1. 118) = 121, 238, 997 in. -lb/min (306 hp) ME 482 - Manufacturing Systems

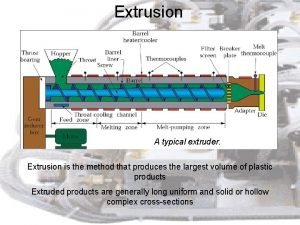
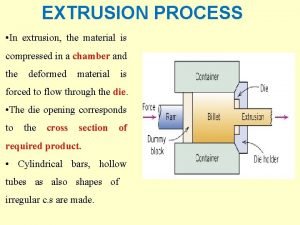
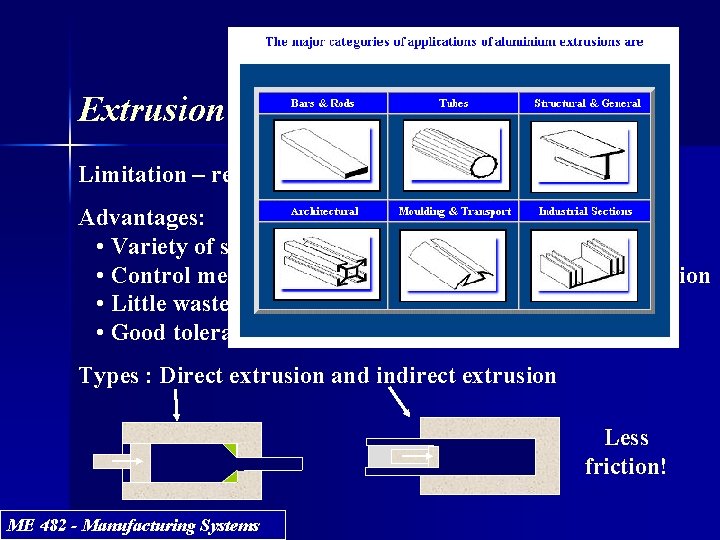
Extrusion Limitation – requires uniform cross-section vs length Advantages: • Variety of shapes • Control mechanical properties in cold and warm extrusion • Little wasted material • Good tolerances Types : Direct extrusion and indirect extrusion Less friction! ME 482 - Manufacturing Systems

Extrusion Model Assumptions: L • Circular cross-section • Uniform stress distribution p Do p = ram pressure L = remaining billet length Do = chamber diameter Df = extrudate diameter ME 482 - Manufacturing Systems Df

Extrusion Model – stress and strain Define extrusion ratio = rx = Ao/Af Ao = billet (chamber) area Af = extrudate area Frictionless model: ideal true strain = e = ln rx ideal ram pressure = p = Yf ln rx With friction: Johnson eqn ex = a + b ln rx ME 482 - Manufacturing Systems a = 0. 8 1. 2 £ b £ 1. 5

Extrusion Model – stress and strain Indirect extrusion ram pressure = p = Yf ex (ex is from Johnson eqn) and where Yf is found using the ideal true strain e = ln rx In direct extrusion, difficult to predict the chamber/billet interactive friction, so use the shear yield strength ( about Yf /2 ) to estimate the chamber wall shear force as pf p Do 2/4 = Yf p Do L/2 giving pf = 2 Y f L / Do and where pf = additional pressure to overcome wall friction force Total ram pressure becomes p = Yf (ex + 2 L / Do ) ME 482 - Manufacturing Systems

Extrusion Model – non-circular sections Apply a shape factor Kx (experimental results): Kx = 0. 98 + 0. 02 (Cx / Cc)2. 25 where Cx = perimeter of extruded shape Cc = perimeter of circle having same area of extruded shape Applies for 1 £ (Cx / Cc) £ 6 For complex extrudate: Indirect Direct p = K x Yf e x p = Kx Yf (ex + 2 L / Do ) ME 482 - Manufacturing Systems

Extrusion Model – forces and power Ram force = F = p. Ao Power = P = Fv ME 482 - Manufacturing Systems

Extrusion example A billet 3” long and 1” diameter is to be extruded as a round extrudate in a direct extrusion operation with extrusion ratio of rx = 4. Given die angle of 90°, strength coefficient of 60, 000 psi, and strain hardening exponent of 0. 18, use the Johnson formula with a = 0. 8 and b = 1. 5 to estimate extrusion strain, and then determine the pressure applied to the end of the billet as the ram moves forward. Solution: e = ln rx = ln 4 = 1. 3863 ex = 0. 8 + 1. 5(1. 3863) = 2. 87945 Yf = 60, 000(1. 386)0. 18/1. 18 = 53, 927 psi ME 482 - Manufacturing Systems

Extrusion example A billet 3” long and 1” diameter is to be extruded as a round extrudate in a direct extrusion operation with extrusion ratio of rx = 4. Given die angle of 90°, strength coefficient of 60, 000 psi, and strain hardening exponent of 0. 18, use the Johnson formula with a = 0. 8 and b = 1. 5 to estimate extrusion strain, and then determine the pressure applied to the end of the billet as the ram moves forward. Solution continued: p = Yf (ex + 2 L/D) = 53, 927 [2. 87945 + (2)(3)/1] p = 478, 842 psi ME 482 - Manufacturing Systems

Rolling and Extrusion What have we learned? ME 482 - Manufacturing Systems
 Rolling and extrusion
Rolling and extrusion Rolling and extrusion
Rolling and extrusion Hot rolling
Hot rolling Roll force formula
Roll force formula Hot rolling
Hot rolling Metal container
Metal container Hot rolling vs cold rolling
Hot rolling vs cold rolling Manufacturing cost vs non manufacturing cost
Manufacturing cost vs non manufacturing cost Manufacturing cost vs non manufacturing cost
Manufacturing cost vs non manufacturing cost Commited cost
Commited cost Manufacturing cost vs non manufacturing cost
Manufacturing cost vs non manufacturing cost Additive manufacturing steps
Additive manufacturing steps Come holy ghost lyrics
Come holy ghost lyrics Comp 482
Comp 482 Comp 482
Comp 482 Engr 482
Engr 482 Comp 482
Comp 482 Comp 482
Comp 482