COMP 482 Design and Analysis of Algorithms Spring

COMP 482: Design and Analysis of Algorithms Spring 2012 Lecture 19 Prof. Swarat Chaudhuri

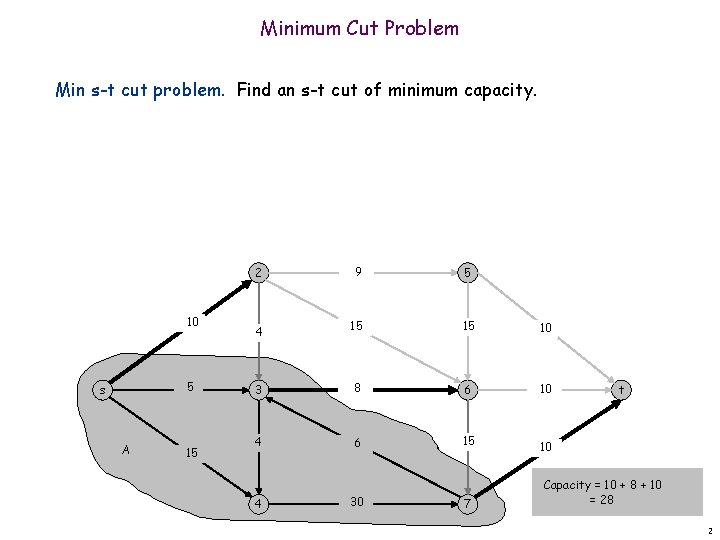
Minimum Cut Problem Min s-t cut problem. Find an s-t cut of minimum capacity. 10 5 s A 15 2 9 5 4 15 15 10 3 8 6 10 4 6 15 4 30 7 t 10 Capacity = 10 + 8 + 10 = 28 2

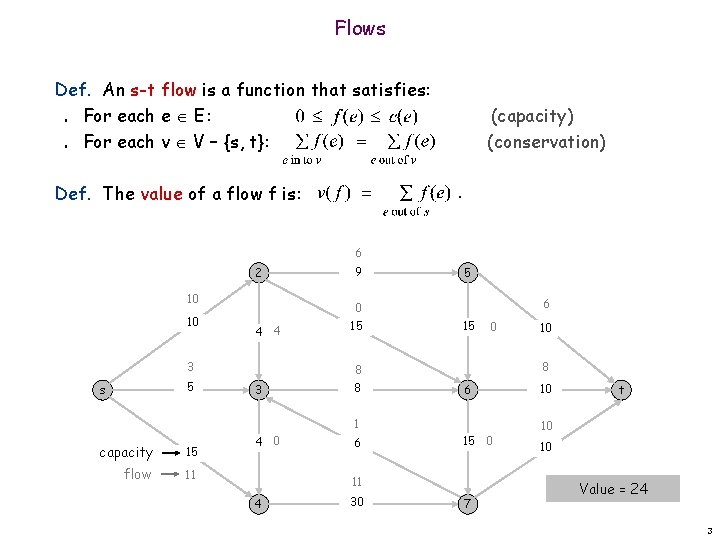
Flows Def. An s-t flow is a function that satisfies: For each e E: For each v V – {s, t}: (capacity) (conservation) n n Def. The value of a flow f is: 6 2 10 10 4 4 3 5 s 9 0 15 5 6 15 0 8 8 3 8 6 1 capacity 15 flow 11 4 0 6 15 0 11 4 30 10 7 10 t 10 10 Value = 24 3

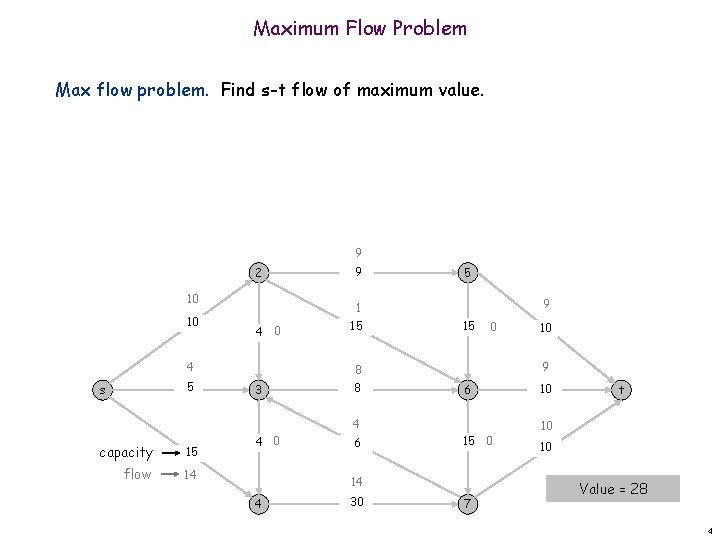
Maximum Flow Problem Max flow problem. Find s-t flow of maximum value. 9 2 10 10 4 5 s 9 1 15 5 9 15 0 9 8 3 8 6 4 capacity 15 flow 14 4 0 6 15 0 14 4 30 10 7 10 t 10 10 Value = 28 4

Augmenting Path Algorithm Augment(f, c, P) { b bottleneck(P) foreach e P { if (e E) f(e) + b else f(e. R) f(e) - b } return f } forward edge reverse edge Ford-Fulkerson(G, s, t, c) { foreach e E f(e) 0 Gf residual graph while (there exists augmenting path P) { f Augment(f, c, P) update Gf } return f } 5

Running Time Assumption. All capacities are integers between 1 and C. Invariant. Every flow value f(e) and every residual capacities c f (e) remains an integer throughout the algorithm. Theorem. The algorithm terminates in at most v(f*) n. C iterations. Pf. Each augmentation increase value by at least 1. ▪ Corollary. If C = 1, Ford-Fulkerson runs in O(mn) time. Integrality theorem. If all capacities are integers, then there exists a max flow f for which every flow value f(e) is an integer. Pf. Since algorithm terminates, theorem follows from invariant. ▪ 6

Recap: Mobile computing Consider a set of mobile computing clients in a certain town who each needed to be connected to one of several base stations. We’ll suppose there are n clients, with the position of each client specified by its (x, y) coordinates. There also k base stations, each of them specified by its (x, y) coordinates as well. For each client, we want to connect it to exactly one of the base stations. We have a range parameter r—a client can only be connected to a base station that is within distance r. There is also a load parameter L—no more than L clients can be connected to a single base station. Your goal is to design a polynomial-time algorithm for the following problem. Given the positions of the clients and base stations as well as the range and load parameters, find the maximum number of clients that can be connected simultaneously to a base station. 7

7. 3 Choosing Good Augmenting Paths

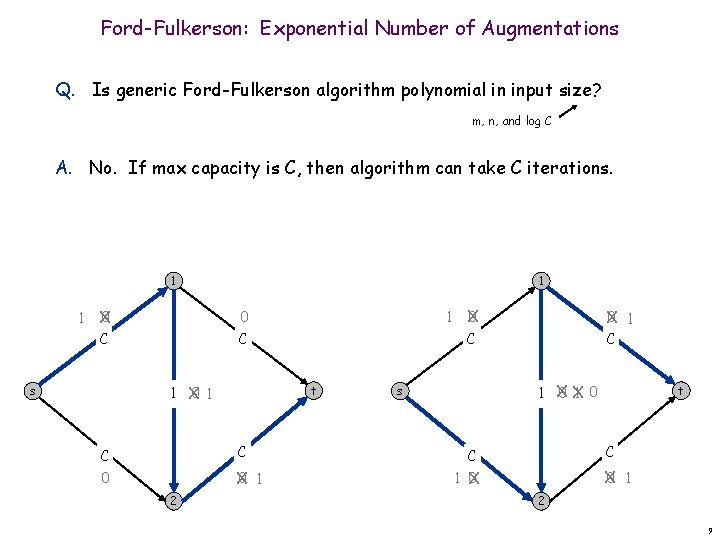
Ford-Fulkerson: Exponential Number of Augmentations Q. Is generic Ford-Fulkerson algorithm polynomial in input size? m, n, and log C A. No. If max capacity is C, then algorithm can take C iterations. 1 1 1 0 X 0 C C 1 X 0 1 s t C C 0 0 1 X 2 1 X 0 0 1 X C C 1 0 1 X 0 X s t C C X 0 1 X 2 9

Choosing Good Augmenting Paths Use care when selecting augmenting paths. Some choices lead to exponential algorithms. Clever choices lead to polynomial algorithms. If capacities are irrational, algorithm not guaranteed to terminate! n n n Goal: choose augmenting paths so that: Can find augmenting paths efficiently. Few iterations. n n Choose augmenting paths with: [Edmonds-Karp 1972, Dinitz 1970] Max bottleneck capacity. Sufficiently large bottleneck capacity. Fewest number of edges. n n n 10

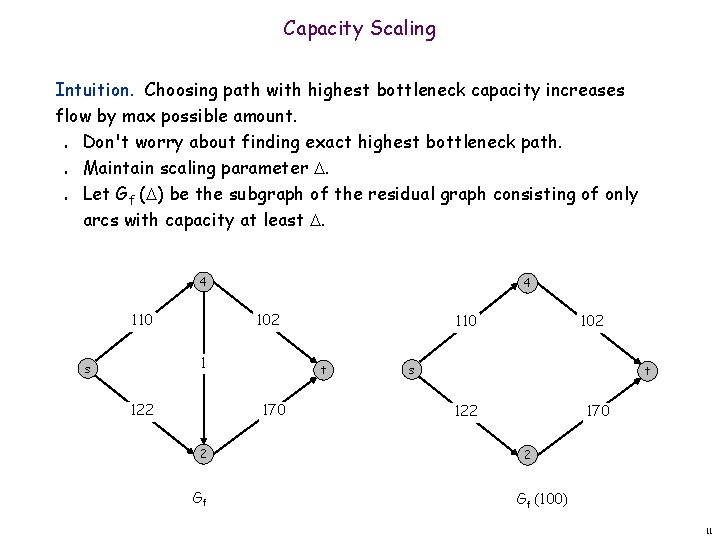
Capacity Scaling Intuition. Choosing path with highest bottleneck capacity increases flow by max possible amount. Don't worry about finding exact highest bottleneck path. Maintain scaling parameter . Let Gf ( ) be the subgraph of the residual graph consisting of only arcs with capacity at least . n n n 4 110 4 102 1 s 122 t 170 2 Gf 110 102 s t 122 170 2 Gf (100) 11

Capacity Scaling-Max-Flow(G, s, t, c) { foreach e E f(e) 0 smallest power of 2 greater than or equal to C Gf residual graph while ( 1) { Gf( ) -residual graph while (there exists augmenting path P in Gf( )) { f augment(f, c, P) update Gf( ) } / 2 } return f } 12

Capacity Scaling: Correctness Assumption. All edge capacities are integers between 1 and C. Integrality invariant. All flow and residual capacity values are integral. Correctness. If the algorithm terminates, then f is a max flow. Pf. By integrality invariant, when = 1 Gf( ) = Gf. Upon termination of = 1 phase, there are no augmenting paths. ▪ n n 13

Capacity Scaling: Running Time Lemma 1. The outer while loop repeats 1 + log 2 C times. Pf. Initially C < 2 C. decreases by a factor of 2 each iteration. ▪ Lemma 2. Let f be the flow at the end of a -scaling phase. Then the proof on next slide value of the maximum flow is at most v(f) + m . Lemma 3. There at most 2 m augmentations per scaling phase. Let f be the flow at the end of the previous scaling phase. L 2 v(f*) v(f) + m (2 ). Each augmentation in a -phase increases v(f) by at least . ▪ n n n Theorem. The scaling max-flow algorithm finds a max flow in O(m log C) augmentations. It can be implemented to run in O(m 2 log C) time. ▪ 14

Capacity Scaling: Running Time Lemma 2. Let f be the flow at the end of a -scaling phase. Then value of the maximum flow is at most v(f) + m . Pf. (almost identical to proof of max-flow min-cut theorem) We show that at the end of a -phase, there exists a cut (A, B) such that cap(A, B) v(f) + m . Choose A to be the set of nodes reachable from s in Gf( ). By definition of A, s A. By definition of f, t A. n n A B t s original network 15

7. 5 Bipartite Matching

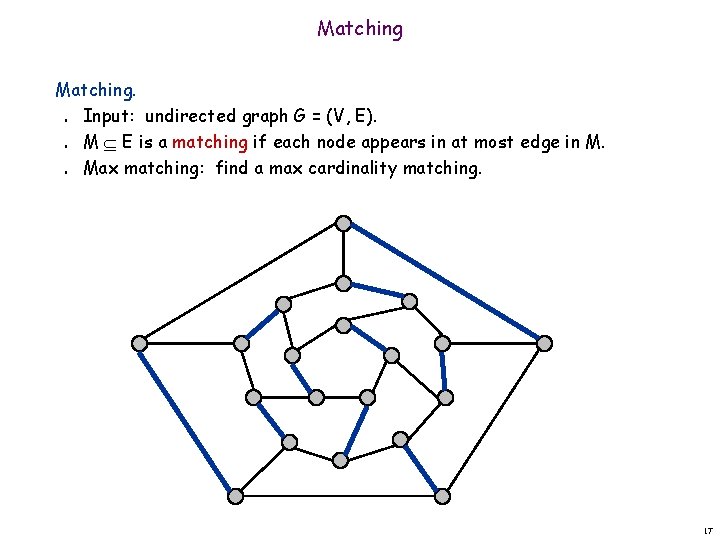
Matching. Input: undirected graph G = (V, E). M E is a matching if each node appears in at most edge in M. Max matching: find a max cardinality matching. n n n 17

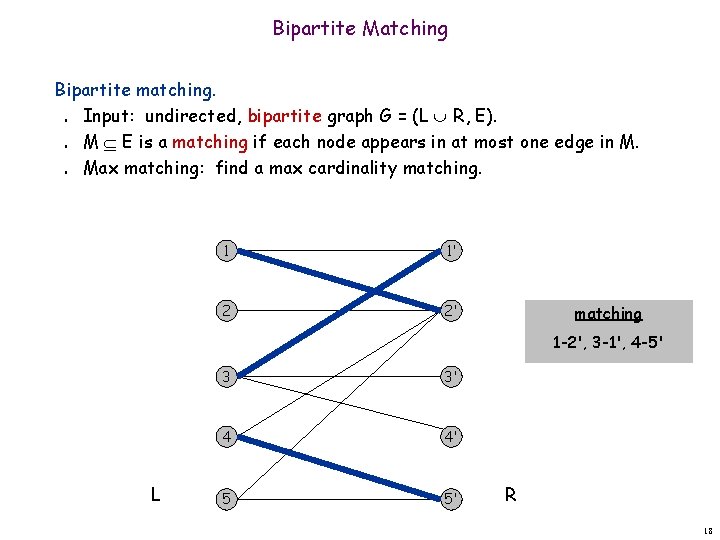
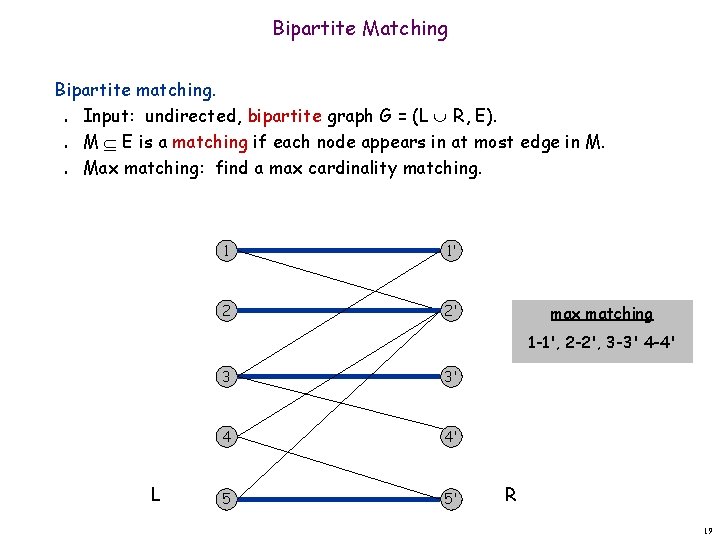
Bipartite Matching Bipartite matching. Input: undirected, bipartite graph G = (L R, E). M E is a matching if each node appears in at most one edge in M. Max matching: find a max cardinality matching. n n n 1 1' 2 2' matching 1 -2', 3 -1', 4 -5' L 3 3' 4 4' 5 5' R 18

Bipartite Matching Bipartite matching. Input: undirected, bipartite graph G = (L R, E). M E is a matching if each node appears in at most edge in M. Max matching: find a max cardinality matching. n n n 1 1' 2 2' max matching 1 -1', 2 -2', 3 -3' 4 -4' L 3 3' 4 4' 5 5' R 19

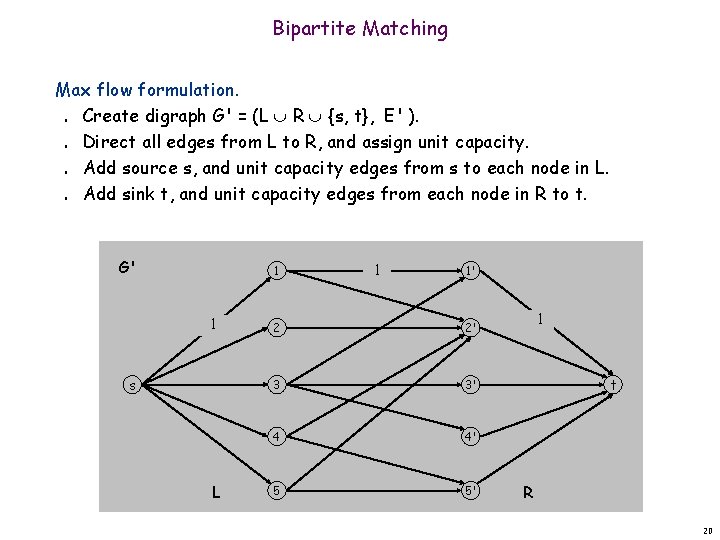
Bipartite Matching Max flow formulation. Create digraph G' = (L R {s, t}, E' ). Direct all edges from L to R, and assign unit capacity. Add source s, and unit capacity edges from s to each node in L. Add sink t, and unit capacity edges from each node in R to t. n n G' 1 1 s L 1 1' 2 2' 3 3' 4 4' 5 5' 1 t R 20

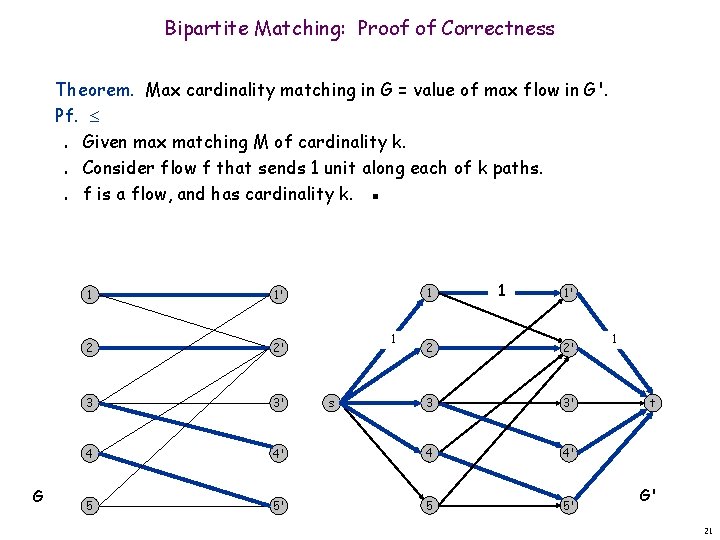
Bipartite Matching: Proof of Correctness Theorem. Max cardinality matching in G = value of max flow in G'. Pf. Given max matching M of cardinality k. Consider flow f that sends 1 unit along each of k paths. f is a flow, and has cardinality k. ▪ n n n G 1 1' 2 2' 3 3' 4 5 1 1' 2 2' 3 3' 4' 4 4' 5' 5 5' s 1 t G' 21

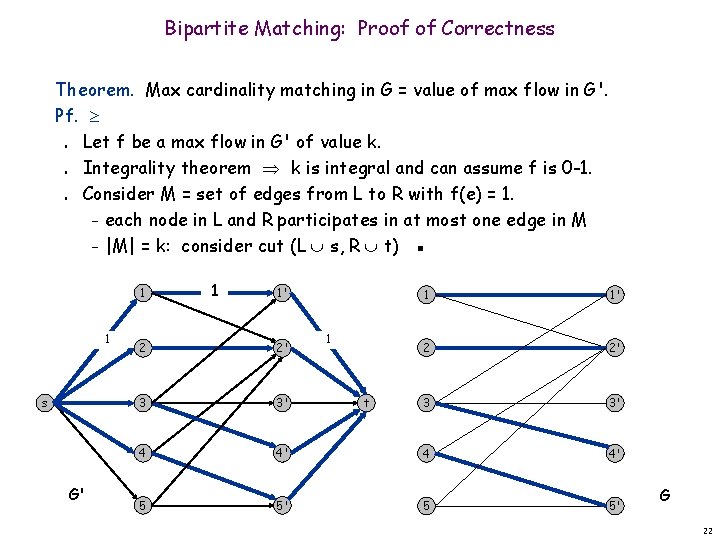
Bipartite Matching: Proof of Correctness Theorem. Max cardinality matching in G = value of max flow in G'. Pf. Let f be a max flow in G' of value k. Integrality theorem k is integral and can assume f is 0 -1. Consider M = set of edges from L to R with f(e) = 1. – each node in L and R participates in at most one edge in M – |M| = k: consider cut (L s, R t) ▪ n n n 1 1 s G' 1 1 1' 2 2' 3 3' 4 4' 5 5' t G 22

Bipartite Matching: Running Time Which max flow algorithm to use for bipartite matching? Generic augmenting path: O(m val(f*) ) = O(mn). Capacity scaling: O(m 2 log C ) = O(m 2). Shortest augmenting path: O(m n 1/2). n n n Non-bipartite matching. Structure of non-bipartite graphs is more complicated, but well-understood. [Tutte-Berge, Edmonds-Galai] Blossom algorithm: O(n 4). [Edmonds 1965] Best known: O(m n 1/2). [Micali-Vazirani 1980] n n n 23

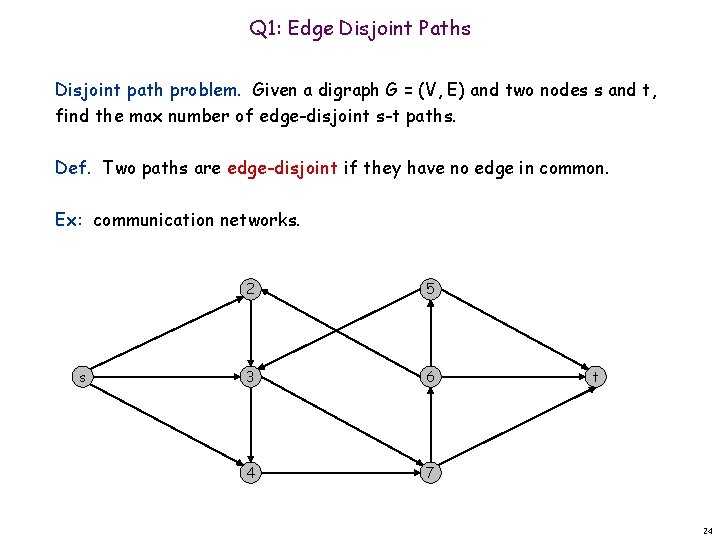
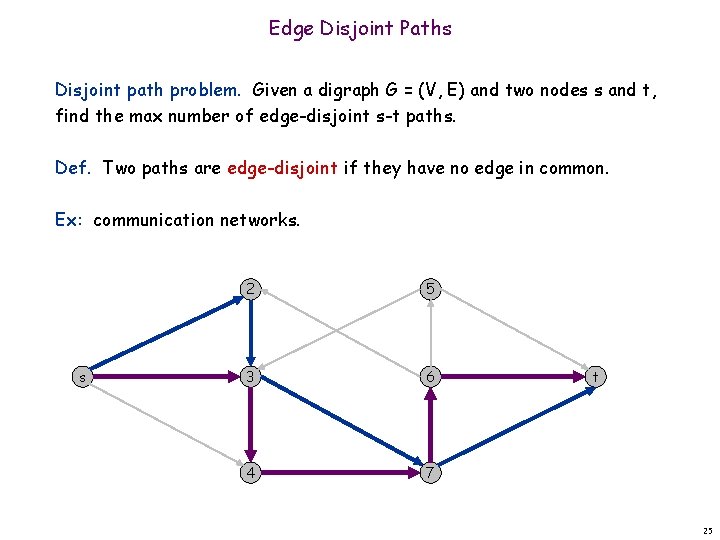
Q 1: Edge Disjoint Paths Disjoint path problem. Given a digraph G = (V, E) and two nodes s and t, find the max number of edge-disjoint s-t paths. Def. Two paths are edge-disjoint if they have no edge in common. Ex: communication networks. s 2 5 3 6 4 7 t 24

Edge Disjoint Paths Disjoint path problem. Given a digraph G = (V, E) and two nodes s and t, find the max number of edge-disjoint s-t paths. Def. Two paths are edge-disjoint if they have no edge in common. Ex: communication networks. s 2 5 3 6 4 7 t 25

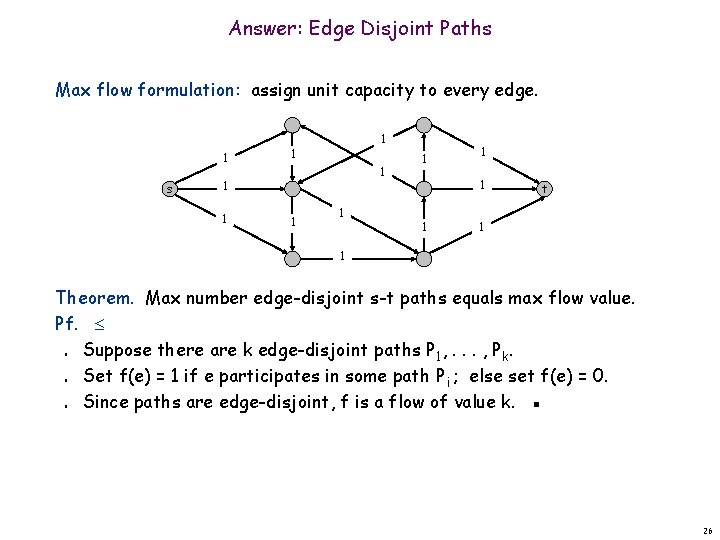
Answer: Edge Disjoint Paths Max flow formulation: assign unit capacity to every edge. 1 s 1 1 1 t 1 1 Theorem. Max number edge-disjoint s-t paths equals max flow value. Pf. Suppose there are k edge-disjoint paths P 1, . . . , Pk. Set f(e) = 1 if e participates in some path Pi ; else set f(e) = 0. Since paths are edge-disjoint, f is a flow of value k. ▪ n n n 26

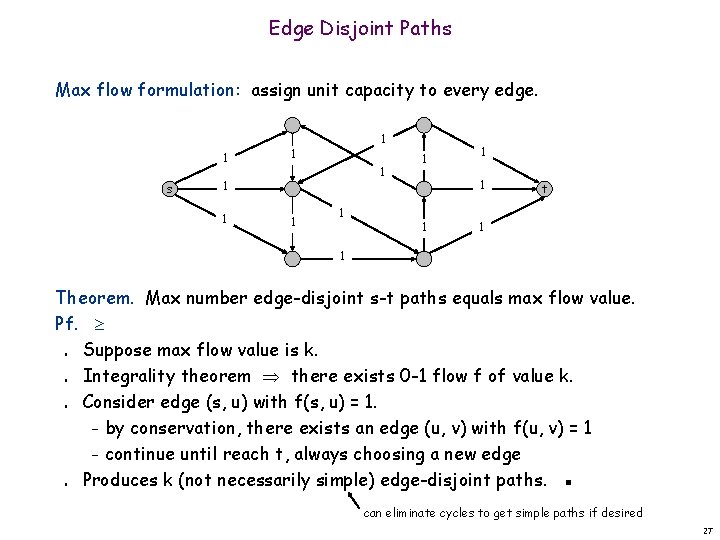
Edge Disjoint Paths Max flow formulation: assign unit capacity to every edge. 1 s 1 1 1 t 1 1 Theorem. Max number edge-disjoint s-t paths equals max flow value. Pf. Suppose max flow value is k. Integrality theorem there exists 0 -1 flow f of value k. Consider edge (s, u) with f(s, u) = 1. – by conservation, there exists an edge (u, v) with f(u, v) = 1 – continue until reach t, always choosing a new edge Produces k (not necessarily simple) edge-disjoint paths. ▪ n n can eliminate cycles to get simple paths if desired 27

Q 2: Project Selection can be positive or negative Projects with prerequisites. Set P of possible projects. Project v has associated revenue p v. n – some projects generate money: create interactive e-commerce interface, redesign web page – n n others cost money: upgrade computers, get site license Set of prerequisites E. If (v, w) E, can't do project v and unless also do project w. A subset of projects A P is feasible if the prerequisite of every project in A also belongs to A. Project selection. Choose a feasible subset of projects to maximize revenue. 31

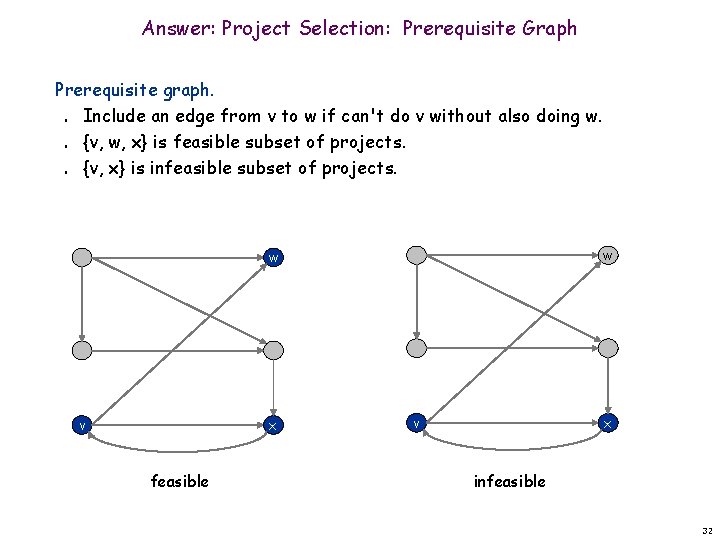
Answer: Project Selection: Prerequisite Graph Prerequisite graph. Include an edge from v to w if can't do v without also doing w. {v, w, x} is feasible subset of projects. {v, x} is infeasible subset of projects. n n n w w v x feasible v x infeasible 32

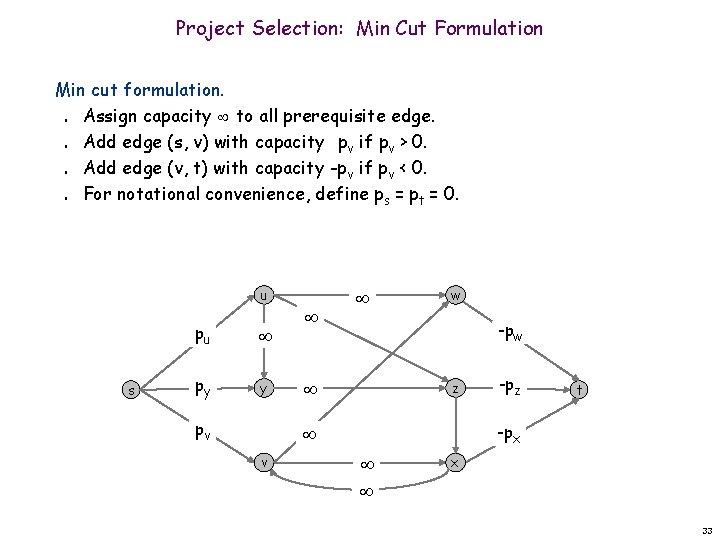
Project Selection: Min Cut Formulation Min cut formulation. Assign capacity to all prerequisite edge. Add edge (s, v) with capacity -pv if pv > 0. Add edge (v, t) with capacity -pv if pv < 0. For notational convenience, define ps = pt = 0. n n u s pu py y pv w -pw z t -px v -pz x 33

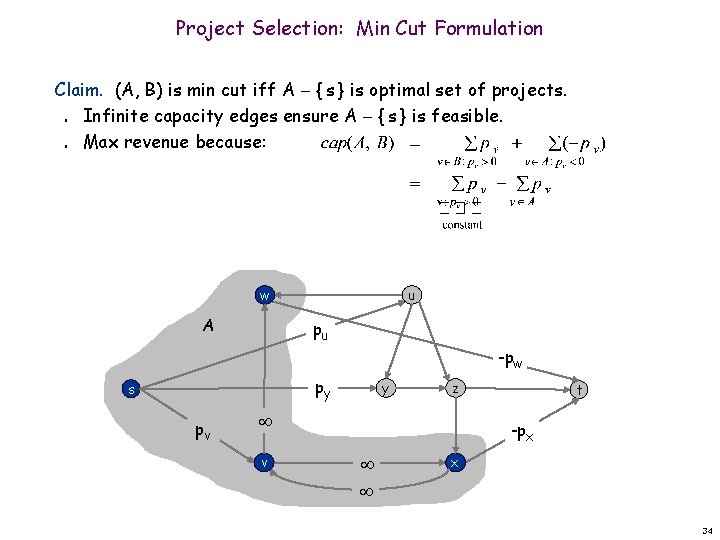
Project Selection: Min Cut Formulation Claim. (A, B) is min cut iff A { s } is optimal set of projects. Infinite capacity edges ensure A { s } is feasible. Max revenue because: n n w A u pu -pw py s pv y z v t -px x 34

Open Pit Mining Open-pit mining. (studied since early 1960 s) Blocks of earth are extracted from surface to retrieve ore. Each block v has net value pv = value of ore - processing cost. Can't remove block v before w or x. n n n w x v 35