Review of search strategies Decisions in games Minimax

• Review of search strategies • Decisions in games • Minimax algorithm • - algorithm • Tic-Tac-Toe game Frequent Asked Questions (FAQ) site: http: //faqs. jmas. co. jp/FAQs/ai-faq/general/part 1 1

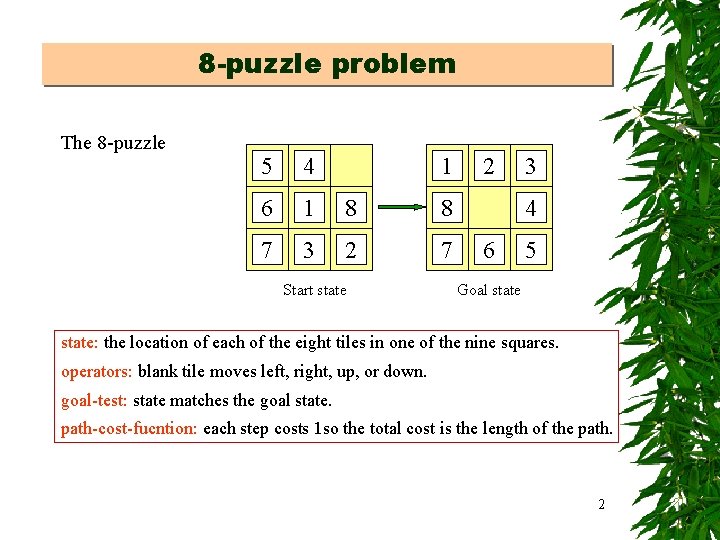
8 -puzzle problem The 8 -puzzle 5 4 1 6 1 8 8 7 3 2 7 Start state 2 3 4 6 5 Goal state: the location of each of the eight tiles in one of the nine squares. operators: blank tile moves left, right, up, or down. goal-test: state matches the goal state. path-cost-fucntion: each step costs 1 so the total cost is the length of the path. 2

Breath-first search The breadth-first search algorithm searches a state space by constructing a hierarchical tree structure consisting of a set of nodes and links. The algorithm defines a way to move through the tree structure, examining the value at nodes. From the start, it looks at each node one edge away. Then it moves out from those nodes to all two edges away from the start. This continues until either the goal node is found or the entire tree is searched. The algorithm follows: 1. Create a queue and add the first node to it. 2. Loop: - If the queue is empty, quit. - Remove the first node from the queue. - If the node contains the goal state, then exit with the node as the solution. - For each child of the current node: add the new state to the back of the queue. 3

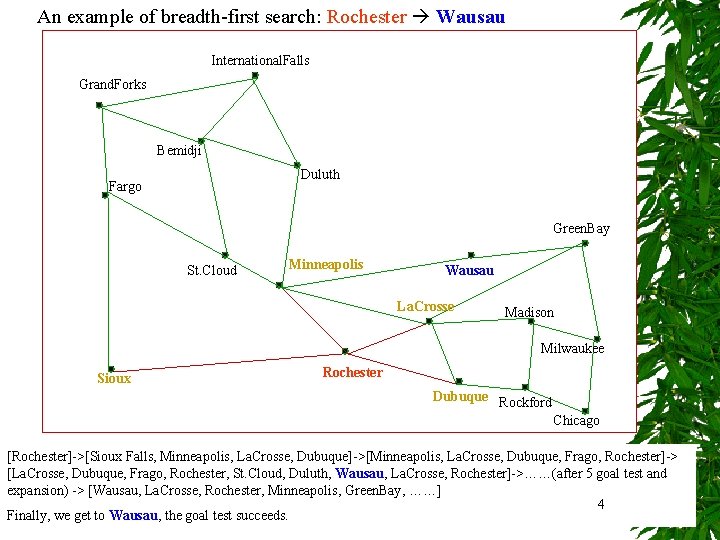
An example of breadth-first search: Rochester Wausau International. Falls Grand. Forks Bemidji Duluth Fargo Green. Bay St. Cloud Minneapolis Wausau La. Crosse Madison Milwaukee Sioux Rochester Dubuque Rockford Chicago [Rochester]->[Sioux Falls, Minneapolis, La. Crosse, Dubuque]->[Minneapolis, La. Crosse, Dubuque, Frago, Rochester]-> [La. Crosse, Dubuque, Frago, Rochester, St. Cloud, Duluth, Wausau, La. Crosse, Rochester]->……(after 5 goal test and expansion) -> [Wausau, La. Crosse, Rochester, Minneapolis, Green. Bay, ……] 4 Finally, we get to Wausau, the goal test succeeds.

Source code for your reference A demo public Search. Node breadth. First. Search(Search. Node initial. Node, Object goal. State) { Vector queue = new Vector() ; queue. add. Element(initial. Node) ; initial. Node. set. Tested(true) ; // test each node once while (queue. size()> 0) { Search. Node test. Node = (Search. Node)queue. first. Element() ; queue. remove. Element. At(0) ; test. Node. trace() ; if (test. Node. state. equals(goal. State)) return test. Node ; // found it if (!test. Node. expanded) { test. Node. expand(queue, Search. Node. BACK) ; } } return null ; } 5

Depth-first search The depth-first algorithm follows a single branch of the tree down as many levels as possible until we either reach a solution or a dead end. It searches from the start or root node all the way down to a leaf node. If it does not find the goal node, it backtracks up the tree and searches down the next untested path until it reaches the next leaf. The algorithm follows: 1. Create a queue and add the first node to it. 2. Loop: - If the queue is empty, quit. - Remove the first node from the queue. - If the node contains the goal state, then exit with the node as the solution. - For each child of the current node: add the new state to the front of the queue. 6

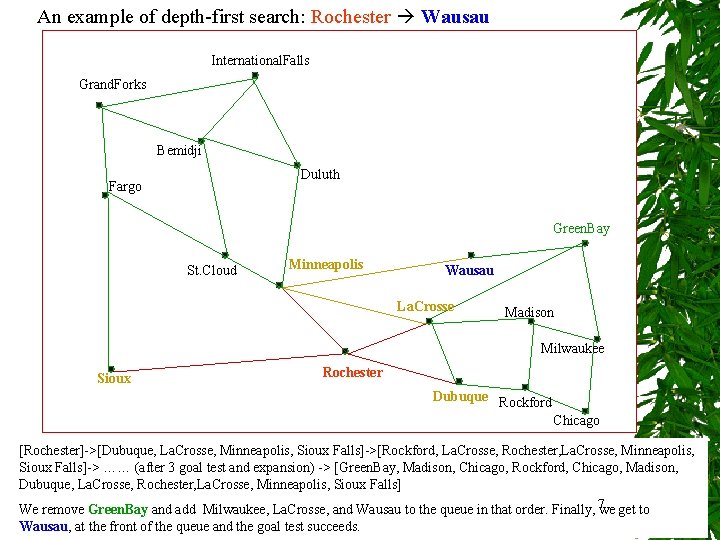
An example of depth-first search: Rochester Wausau International. Falls Grand. Forks Bemidji Duluth Fargo Green. Bay St. Cloud Minneapolis Wausau La. Crosse Madison Milwaukee Sioux Rochester Dubuque Rockford Chicago [Rochester]->[Dubuque, La. Crosse, Minneapolis, Sioux Falls]->[Rockford, La. Crosse, Rochester, La. Crosse, Minneapolis, Sioux Falls]-> …… (after 3 goal test and expansion) -> [Green. Bay, Madison, Chicago, Rockford, Chicago, Madison, Dubuque, La. Crosse, Rochester, La. Crosse, Minneapolis, Sioux Falls] We remove Green. Bay and add Milwaukee, La. Crosse, and Wausau to the queue in that order. Finally, 7 we get to Wausau, at the front of the queue and the goal test succeeds.

Source code for your reference A demo public Search. Node depth. First. Search(Search. Node initial. Node, Object goal. State) { Vector queue = new Vector() ; queue. add. Element(initial. Node) ; initial. Node. set. Tested(true) ; // test each node once while (queue. size()> 0) { Search. Node test. Node = (Search. Node)queue. first. Element() ; queue. remove. Element. At(0) ; test. Node. trace() ; // display trace information if (test. Node. state. equals(goal. State)) return test. Node ; // found it if (!test. Node. expanded) { test. Node. expand(queue, Search. Node. FRONT); } } return null ; } 8

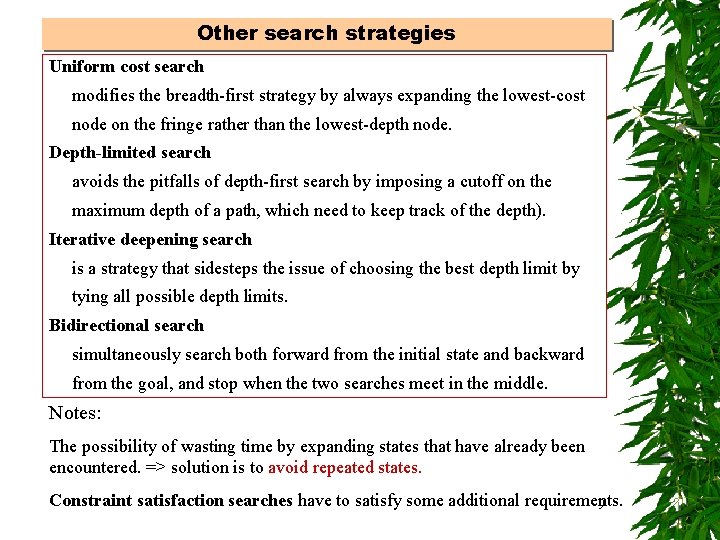
Other search strategies Uniform cost search modifies the breadth-first strategy by always expanding the lowest-cost node on the fringe rather than the lowest-depth node. Depth-limited search avoids the pitfalls of depth-first search by imposing a cutoff on the maximum depth of a path, which need to keep track of the depth). Iterative deepening search is a strategy that sidesteps the issue of choosing the best depth limit by tying all possible depth limits. Bidirectional search simultaneously search both forward from the initial state and backward from the goal, and stop when the two searches meet in the middle. Notes: The possibility of wasting time by expanding states that have already been encountered. => solution is to avoid repeated states. Constraint satisfaction searches have to satisfy some additional requirements. 9

Informed Search Methods Best-first search is that the one node with the best evaluation is expanded. Nodes to be expanded are evaluated by an evaluation function. Greedy search is a best-first search that uses an estimated cost of the cheapest path from that state at node n to a goal state to select the next node to expand. A function that calculates such cost estimates is called a heuristic function. Memory bounded search applies some techniques to reduce memory requirement. Hill-climbing search always tries to make changes that improve the current state. (it may find a local maximum) Simulated annealing allow the search to take some downhill steps to escape the local maximum For example, For 8 -puzzle problem, two heuristic functions, h 1 = the number of tiles that are in the wrong position, h 2 = the sum of the distance of the tiles from their goal positions. Is it possible for a computer to mechanically invent a better one? 10

Games as search problems Game playing is one of the oldest areas of endeavor in AI. What makes games really different is that they are usually much too hard to solve within a limited time. For chess game: there is an average branching factor of about 35, games often go to 50 moves by each player, so the search tree has about 35100 (there are only 1040 different legal position). The result is that the complexity of games introduces a completely new kind of uncertainty that arises not because there is missing information, but because one does not have time to calculate the exact consequences of any move. In this respect, games are much more like the real world than the standard search problems. But we have to begin with analyzing how to find theoretically best move in a game problem. Take a Tic-Tac-Toe as an example. 11

Perfect two players game Two players are called MAX and MIN. MAX moves first, and then they take turns moving until the game is over. The problem is defined with the following components: • initial state: the board position, indication of whose move, • a set of operators: legal moves. • a terminal test: state where the game has ended. • an utility function, which give a numeric value, like +1, -1, or 0. So MAX must find a strategy, including the correct move for each possible move by Min, that leads to a terminal state that is winner and the go ahead make the first move in the sequence. Notes: utility function is a critical component that determines which is the best move. 12

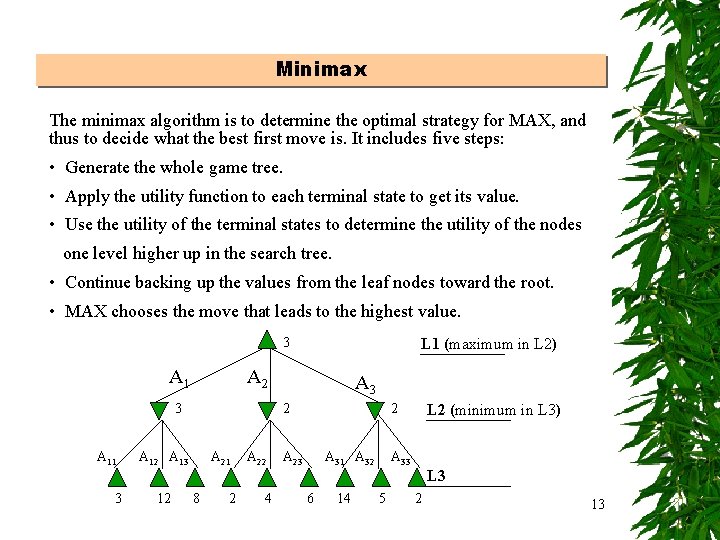
Minimax The minimax algorithm is to determine the optimal strategy for MAX, and thus to decide what the best first move is. It includes five steps: • Generate the whole game tree. • Apply the utility function to each terminal state to get its value. • Use the utility of the terminal states to determine the utility of the nodes one level higher up in the search tree. • Continue backing up the values from the leaf nodes toward the root. • MAX chooses the move that leads to the highest value. 3 A 1 A 2 3 A 11 L 1 (maximum in L 2) A 3 2 A 13 A 21 A 22 2 A 23 A 31 A 32 L 2 (minimum in L 3) A 33 L 3 3 12 8 2 4 6 14 5 2 13

Minimax algorithm function Minmax-Decision(game) returns an operator for each op in Operators[game] do Value[op] Minmax-Value(Apply(op, game) end return the op with the highest Value[op] function Minmax-Value(state, game) returns an utility value if Terminal-Test[game](state) then return Utility[game](state) else if MAX is to move in state then return the highest Minimax-Value of Successors(state) else return the lowest Minimax-Value of Successors(state) 14

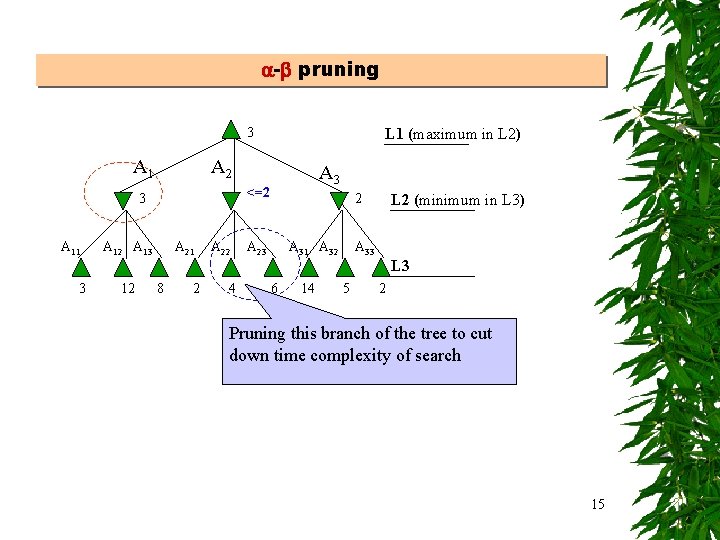
- pruning 3 A 1 A 2 A 3 <=2 3 A 11 L 1 (maximum in L 2) A 12 A 13 A 21 A 22 2 A 23 A 31 A 32 L 2 (minimum in L 3) A 33 L 3 3 12 8 2 4 6 14 5 2 Pruning this branch of the tree to cut down time complexity of search 15

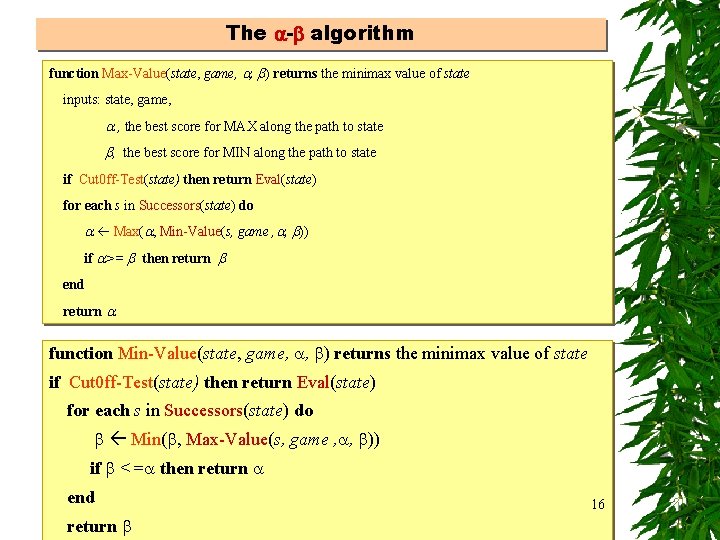
The - algorithm function Max-Value(state, game, , ) returns the minimax value of state inputs: state, game, , the best score for MAX along the path to state , the best score for MIN along the path to state if Cut 0 ff-Test(state) then return Eval(state) for each s in Successors(state) do Max( , Min-Value(s, game , , )) if >= then return end return function Min-Value(state, game, , ) returns the minimax value of state if Cut 0 ff-Test(state) then return Eval(state) for each s in Successors(state) do Min( , Max-Value(s, game , , )) if <= then return end return 16

Tic Tac Toe game public Position put() { if (finished) { return new Position(-1, -1); } Sym. Tic st_now = new Sym. Tic(tic, get. Using. Char()); st_now. evaluate(depth, Sym. Tic. MAX, 999); Sym. Tic st_next = st_now. get. Max. Child(); Position pos = st_next. get. Position(); return pos; } Download site: http: //www. nifty. com/download/other/java/game/index_03. htm 17

Tic Tac Toe game else { int min. Value = 999; Vector v_child = this. children('o'); // 評価する. for (int i=0; i<v_child. size(); i++) { public int evaluate(int depth, int level, int ref. Value) { Sym. Tic st = (Sym. Tic)v_child. element. At(i); int e = evaluate. Myself(); int value = st. evaluate(depth-1, MAX, min. Value); if ((depth==0)||(e==99)||(e==-99)||((e==0)&&(Judge. finished(this)))) { if (value < min. Value) { return e; min. Value = value; } else if (level == MAX) { } int max. Value = -999; if (value <= ref. Value) { Vector v_child = this. children(using. Char); return value; for (int i=0; i<v_child. size(); i++) { } } Sym. Tic st = (Sym. Tic)v_child. element. At(i); int value = st. evaluate(depth, MIN, max. Value); if (max. Value < value) { max. Child = st; max. Value = value; return min. Value; }} private int evaluate. Myself() { char c = Judge. winner(this); if (c == using. Char) { } return 99; if (ref. Value <= value) { return value; } else if (c != ' ') { return -99; } } } else if (Judge. finished(this)) { return 0; return max. Value; } } 18

Exercises Ex 1. What makes games different from the standard search problems? Ex 2. Why is minimax algorithm designed to determine the optimal strategy for MAX? If MIN does not play perfectly to minimize MAX utility function, what may happen. ? Ex 3. Why is - malgorithm is more efficient than minimax algorithm, please explain it. Ex 4. Can you write your own version of Java program that implements minimax algorithm for Tic-Tac-Toe (3 x 3) game (optional) 19