REPASO 7 3 1 contraccin de longitudes y

REPASO 7. 3. 1. contracción de longitudes y dilatación de tiempos. Veamos un par de consecuencias de las ecuaciones de transformación de Lorentz I. Una primera consecuencia es ésta: II. Entonces, el intervalo de tiempo propio es el intervalo de tiempo que hay entre dos eventos que ocurren en el mismo lugar en un sistema ( S o S‘), o bien, el intervalo de tiempo medido con el mismo reloj en un solo lugar.

Advertencia I: Por el contrario, lo que se debe hacer es tomar la resta de las posiciones transformadas por la fórmula de Lorentz. Advertencia II:

7. 3. 2. Diagramas espacio-tiempo (representación geométrica del espacio-tiempo). En física clásica, la coordenada del tiempo no es afectada por una transformación de un sistema inercial a otro. La coordenada del tiempo, t', de un sistema inercial no depende de las coordenadas espaciales, x, y, z de otro sistema inercial, siendo la ecuación de transformación t' = t. Sin embargo, en relatividad, el espacio y el tiempo son interdependientes. La coordenada del tiempo de un sistema inercial depende tanto del tiempo como de la coordenada espacial de otro sistema inercial, siendo la ecuación de transformación Luego, en lugar de tratar al espacio y al tiempo separadamente, como se realiza en la teoría clásica, en relatividad debemos tratarlos en conjunto. El matemático alemán Hermann Minkowski fue el primero en demostrar claramente cómo se podía hacer esto A continuación, se considerará solamente un eje espacial, el eje x y se ignorará los ejes y y z. No se perderá generalidad por esta simplificación algebraica y este ·procedimiento nos permitirá representar más claramente la interdependencia del espacio y el tiempo y su representación geométrica. Entonces, las coordenadas de un evento están dadas por x y t. Es conveniente conservar las dimensiones de las coordenadas iguales; esto es inmediato multiplicando el tiempo t por la constante universal c, la velocidad de la luz; se representará entonces ct por el símbolo w (y a v/c por b ). Entonces, las ecuaciones de transformación de Lorentz pueden escribirse como:

Para representar la situación geométricamente, se comienza trazando los ejes x y w del sistema S perpendiculares entre sí. Si se desea representar el movimiento de una partícula en este sistema, se traza una curva, denominada línea de mundo, que da· el lugar geométrico de los puntos espacio-tiempo correspondientes al movimiento. La tangente a la línea de mundo en cualquier punto, es está inclinada con respecto al eje del tiempo en un ángulo que es menor de 45°. Ello se debe a que este ángulo está La línea de mundo de un pulso de luz, para la cual u = c es una recta a 45° con los ejes. Se considera ahora el sistema (S') que se mueve con respecto a S, desplazándose a una velocidad v a lo largo del eje común x -x'. La ecuación de movimiento de S' con respecto a S puede obtenerse haciendo x' = 0 (lo cual localiza el origen de S'); de la ecuación para x’, tenemos que esto corresponde a x = bw (= vt). Se traza la línea x' =0 (es decir x = bw ) en el diagrama de la derecha y considerando que v < c y (b < 1, el ángulo que esta línea forma con el w, f = arctg (b), es menor que 45°. Del mismo modo que el eje w corresponde a x = 0 y es el eje del tiempo en el sistema S, así la línea x' = 0 da el eje del tiempo w' en S'. De la ecuación para w’, w' = 0 significa que w = bx es la ecuación de este eje en el diagrama w - x Es fácil demostrar que el ángulo entre los ejes espaciales es el mismo que el de los ejes temporales, f = arctg (b).

Del diagrama de los dos sistemas de coordenadas, se nota que en el espacio en dos dimensiones (x, t) las ecuaciones de Lorentz, implican la transformación de un sistema ortogonal a un sistema no ortogonal. Se puede usar esta representación para mostrar en forma muy sencilla la relatividad de la simultaneidad Relatividad de la simultaneidad Medidos en S', dos eventos serán simultáneos si tienen la misma coordenada w' del tiempo. Por lo tanto, si los eventos ocurren sobre una paralela al eje x' son simultáneos en S'. Por ejemplo, en la figura de la derecha, los eventos Q 1 y Q 2 son simultáneos en S', obviamente no son simultáneos en S, ocurriendo·en tiempos diferentes w 1 y w 2 en dicho sistema. De manera semejante, dos eventos R 1 y R 2 que son simultáneos en S, no lo son en S'.

Esta representación geométrica de las transformaciones de Lorentz también ayudan a visualizar y entender los efectos de contracción del espacio y de dilatación del tiempo, así como ilustrar su naturaleza recíproca. Para hacer esto sin embargo precisamos trabajar un poco más e introducir las llamadas curvas de calibración de unidades. Curvas de calibración: Comencemos trazando las dos ramas de la Comparando con las ecuaciones transformación, vemos que la primera repre- Comparando con las ecuaciones transformación, vemos que la primera representa

Ejercicio. Muestre que la unidad de distancia espacio-temporal en el sistema S, u (unidad en que se miden distancias en las dimensiones x o w ), esta relacionada con la u’ de S’ por:

Contracción de las longitudes medidas para objetos en movimiento En el sistema en reposo S la longitud es la distancia entre las intersecciones de las líneas de mundo con el eje x, o cualquier línea paralela al eje x, porque estos puntos de intersección representan eventos simultáneos en S. La longitud en reposo es de 1 metro. Para calcular la longitud en S', que se mueve con b = 0. 5, en el que la varilla se mueve, se debe determinar la distancia en S' entre los puntos extremos midiéndolos simultáneamente. A-7 Esta será la separación en S' de las intersecciones de la línea de mundo con el eje x', o cualquier recta paralela al eje x', ya que estos puntos de intersecciones representan eventos simultáneos en S'. Obviamente, la longitud de la varilla (en movimiento) es menor que un metro en S' (como se muestra en la Fig. A-7 a). Ejercicio. Usando la formula De hecho la podemos calcular fácilmente: que conecta a la unidades de distancia espacio-temporal en S y S’ y que el ángulo f = arctg (b) muestre que la longitud de la varilla medida en S’ es de aprox. 0. 87 m. Lo verificamos usando la formula:

Dilatación del tiempo medido por relojes en movimiento Para demostrar geométricamente el resultado de la dilatación del tiempo consideremos a la Fig. A-8. Se supone un reloj en reposo en el sistema S, dando el tiempo ahí. La línea continua vertical en la Fig. A-8, en x = 2. 3, es la línea de mundo correspondiente a tal reloj. T 1 y T 2 son los eventos transcurridos en w (= ct) = 2 y w (= ct) = 3, siendo igual a uno el intervalo de tiempo en S entre dichos eventos. En S', este reloj se encuentra en movimiento hacia la izquierda de modo que los eventos de dar la hora se suceden en lugares distintos. Para medir el intervalo de tiempo entre los eventos T 1 y T 2 en S', se usan dos relojes diferentes, uno situado en el lugar de T 1 y el otro en el lugar de T 2. La diferencia en lecturas de estos relojes en S' es la diferencia en el tiempo entre T 1 y T 2 medidos en S'. A partir de la gráfica, se nota que este intervalo es mayor que la unidad. Por consiguiente, desde el punto de vista de S', el reloj en movimiento parece marchar más lentamente. Durante el intervalo que el reloj S registró la unidad de tiempo, el reloj S' registró un tiempo mayor que la unidad. Finalmente, la naturaleza recíproca del resultado de la dilatación del tiempo se muestra también en la Fig. A-8. El estudiante debe proponer un razonamiento detallado. Aquí un reloj en reposo en S' emite señales en U 1 y U 2 separados por la unidad de tiempo propio. Al medirse en S, el intervalo correspondiente de tiempo excede la unidad.

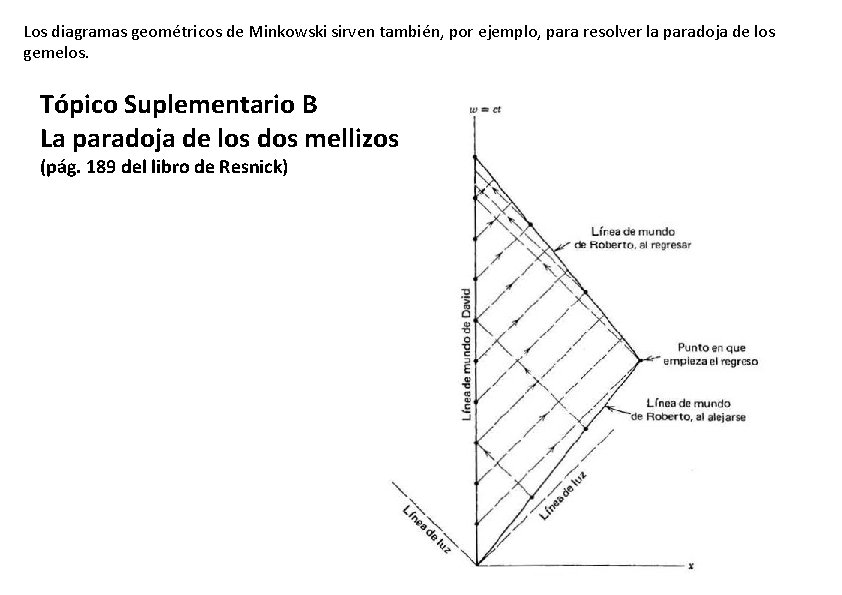
Los diagramas geométricos de Minkowski sirven también, por ejemplo, para resolver la paradoja de los gemelos. Tópico Suplementario B La paradoja de los dos mellizos (pág. 189 del libro de Resnick)

7. 4 CINEMATICA RELATIVISTA Formula de adición relativista de velocidades ¿Cuál es la. velocidad del pasajero, observada desde tierra? Utilizando las ecuaciones de transformación de Lorentz, tenemos Reagrupando los términos proporcionales a x y a t podemos escribir Y, teniendo en cuenta que x =u t nos queda

Veamos dos verificaciones de que la formula relativista de adición de velocidades da resultados consistentes con lo que sabemos y con los postulados. I. Si u' y v son muy pequeñas comparadas con c, en la ecuación el segundo término del denominador es despreciable comparado con uno y entonces se reduce al resultado clásico: u =u' + v II. Si u' =c, siempre debe obtenerse que u =c; significaría que el "pasajero" es un pulso de luz y sabemos que este resultado fue exactamente uno de los postulados de Einstein. Si tomamos u' =c se obtiene Por lo tanto, cualquier velocidad (menor a c) relativistamente sumada a c da una resultante c. Hasta el momento, hemos considerado únicamente la transfonnación de velocidades paralelas a la dirección del movimiento relativo de los dos sistemas de referencia (la dirección x-x'). Para expresar esto, debemos poner subíndices x para u y u' en la ecuación de suma de velocidades, obteniendo Para velocidades perpendiculares a la dirección del movimiento relativo, el resultado es más complicado.

Imaginemos que un objeto se mueve paralelamente al eje y' de S’. Exactamente de la misma manera encontramos que Juntando todo nos quedan las siguientes formulas: