Regressziszmts 2 ht Regressziszmts clja Az analitikus regressziszmts

Regresszió-számítás 2. hét

Regressziószámítás célja Az analitikus regressziószámítás célja, a tényezőváltozónak az eredményváltozóra gyakorolt hatását matematikai modell segítségével fejezze ki. A matematikai modellben specifikáljuk az analitikus regressziófüggvényt. A sztochasztikus kapcsolatban megnyilvánuló törvényszerűség kifejezési formája.

Regresszió-függvények A statisztikai gyakorlatban leggyakrabban a előforduló függvények: q lineáris regresszió, q hatványkitevős regresszió, q exponenciális regresszió, q parabolikus regresszió, q hiperbolikus regresszió.

Az összefüggés–vizsgálatok általános menete q q q q q célkitűzések megfogalmazása, adatbázis megteremtése, függvény – specifikáció (függvény típusának kiválasztása), a kiválasztott függvény paramétereinek számítása, illeszkedésvizsgálat, szignifikancia-vizsgálatok (a modell és a paraméterek tesztelése), a regressziós értékek konfidencia határainak a megállapítása, elaszticitás (rugalmasság) meghatározása, korrelációszámítás (lineáris esetben a korreláció-számítás megelőzheti a regresszió-analízist), az eredmények értelmezése.

A lineáris regresszió modellje Legyen X egy tényezőváltozó és Y egy eredményváltozó. q Tételezzük fel, hogy X lineáris törvényszerűség szerint fejti ki hatását Y-ra, illetve közrejátszik egy véletlen mozzanat is. q A két változó kapcsolatának a formulája: regressziós együtthatók véletlen változó

Lineáris regressziós modell feltételei A változók közötti kapcsolat lineáris: Y változó megfelelő X -hez tartozó értéke X lineáris függvénye. Y/X=β 0+ β 1 X+ ε/X q A magyarázó változó(k) nem valószínűségi változó(k). q Sztochasztikus specifikáció (maradékváltozó tulajdonságai): q A maradékváltozók feltételes várható értéke 0: E(ε/X)=0 § A maradékváltozók feltételes varianciája legyen állandó (homoszkedaszticitási feltétel): Var(ε/X)=σ2 § A maradékváltozó különböző X-értékekhez tartozó értékei legyenek korrelálatlanok: Cov(ε/Xi, ε/Xi’)=0, ha i≠i’ § A maradékváltozó feltételes eloszlásai legyenek normálisak. §

A regressziós együtthatók becslése lineáris regresszió ismeretlen 0 és 1 paramétereinek becsléséhez kizárólag az (xi, yi) adatpárokkal (megfigyelési eredményekkel) rendelkezünk. q Jelöljük a regressziós együtthatók becsléseit rendre b 0 és b 1 szimbólumokkal, a becsült regressziófüggvény pedig legyen: q. A

Regressziós együtthatók becslése A i feltételes várható érték becslése valamely rögzített X = xi helyen ennek megfelelően A becsült regressziós együtthatók kiszámításához a legkisebb négyzetek módszerét fogjuk alkalmazni.

A regressziós becslés normálegyenletei A legkisebb négyzetek módszere szerint azzal az egyenessel becsüljük a lineáris regressziófüggvényt, amelyre nézve a négyzetösszeg a legkisebb értékét veszi fel.

A regresszió-függvények fontosabb tulajdonságai q q A regressziós együtthatók becslése torzítatlan: M(b 0) = 0 és M(b 1) = 1 A feltételes várható érték torzítatlan becslése M( ŷi) = i A b 0 és b 1 a regressziós paraméterek legjobb lineáris torzítatlan becslései, abban az értelemben, hogy legkisebb a szórásuk (standard hibájuk). Ez az ún. Gauss-Markov-tétel. Ha a lineáris regressziós modell feltételeihez még azt is csatoljuk, hogy a véletlen változó normális eloszlást követ, akkor levezethetők a 0 és 1 maximum likelihood becslései is, amelyek azonosak a legkisebb négyzetek módszeréből származó becslő formulákkal.

Az eredmények értelmezése q A b 0 regressziós együttható jelentőségét az adja meg, hogy az X = 0 helyen a függvény éppen ezt az értéket veszi fel. Értelmezése tehát attól függ, hogy a nulla beletartozik -e azon X értékek halmazába, amelyből a regressziót számítottuk, vagy legalábbis logikailag az értelmezési tartomány részének tekinthető-e? q A b 1 regressziós együttható geometriai értelemben az egyenes meredekségét meghatározó iránytangens, azaz dy/dx. A korrelációs kapcsolat elemzésekor ebből azt olvashatjuk le, hogy a tényezőváltozó egységnyi változása mekkora hatással jár együtt az eredményváltozóban.

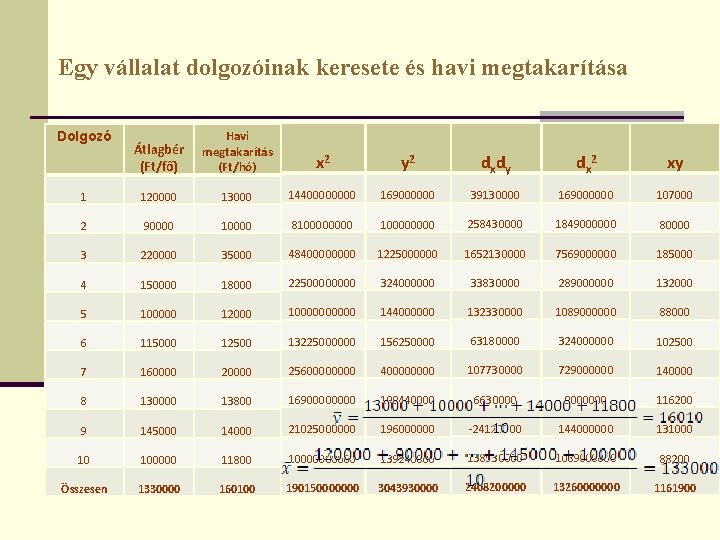
Egy vállalat dolgozóinak keresete és havi megtakarítása Átlagbér (Ft/fő) Havi megtakarítás (Ft/hó) x 2 y 2 dx dy dx 2 xy 1 120000 13000 1440000 169000000 39130000 169000000 107000 2 90000 10000 8100000000 258430000 1849000000 80000 3 220000 35000 4840000 1225000000 1652130000 7569000000 185000 4 150000 18000 2250000 324000000 33830000 289000000 132000 5 100000 12000 100000 144000000 132330000 1089000000 88000 6 115000 12500 13225000000 156250000 63180000 324000000 102500 7 160000 2560000 40000 107730000 729000000 140000 8 130000 13800 1690000 190440000 6630000 9000000 116200 9 145000 14000 21025000000 196000000 -24120000 144000000 131000 10 100000 11800 100000 139240000 138930000 1089000000 88200 Összesen 1330000 160100 190150000000 3043930000 2408200000 13260000000 1161900 Dolgozó

Mintapélda megoldása Bér (Ft/fő) Havi megtakarítás (Ft/hó) x 2 y 2 dx dy dx 2 xy … … … … Összesen 1330000 160100 190150000000 3043930000 2408200000 13260000000 1161900 Dolgozó Regressziós paraméterek értékei: b 0=-8144, 65 b 1=0, 1816 Regressziós egyenes: ŷ= =-8144, 65+0, 1816 x Regressziós paraméterek értelmezése: b 0=ha dolgozók bére 0 Ft, akkor a havi megtakarítás összege -8144, 65 Ft: nem értelmezzük!!! b 1=ha a dolgozók bére havonta 1 Ft-tal növekedne, akkor a havi megtakarítás összege 0, 1816 Ft-tal növekedne.

Az elaszticitás fogalma A rugalmasság mérőszáma arra ad választ, hogy Y relatív változása (növekménye) hányszorosa az X relatív változásának (pl. egyszázalékos X növekményre hány százalék Y növekmény jut). A lineáris regresszió elaszticitása Az elaszticitás átlagos szinten:

Elaszticitás a mintapélda alapján Értelmezés: ha dolgozók keresete 1%-kal növekszik, akkor a havi megtakarított összeg átlagosan 1, 51%-kal növekszik.

Nemlineáris regresszió

Hatványkitevős regresszió A hatványkitevős regressziós összefüggés a társadalmi-gazdasági életben gyakran előfordul. Ezt figyelhetjük meg például a háztartások jövedelme és a fogyasztási kiadásai között. A hatványfüggvény általános képlete: Az „a” paramétert a gyakorlatban nem értelmezzük, a „b” paramétert rugalmassági (elaszticitási) együtthatónak is nevezzük. Jelentése: „x” egy százalékos változása, „y” hány százalékos változását vonja maga után. Ez hasonló a lineáris esetben számított rugalmassági együtthatóhoz, de ez minden „x” esetén ugyanannyi. A hatványfüggvény lefutása a „b” paraméter értékétől függ.

A függvény átalakítása A hatványfüggvény lineárissá alakítható logaritmálás segítségével, így az átalakítás után alkalmazhatóak a lineáris függvénynél alkalmazott ismeretek. A logaritmizálás után a következő összefüggést kapjuk: Az átalakítás után nem „x”-ek és „y”-ok között van lineáris kapcsolat, hanem log „y”-ek és log „x”-ek között, tehát nincs más dolgunk, mint az eredeti változók logaritmusát képezni, és ezek között keresni a lineáris kapcsolatot.

Paraméterek értelmezése – grafikus ábrák által Ha b 1, akkor rugalmas (vagy gyorsuló növekedésű) hatványfüggvényről beszélünk. A rugalmas hatványfüggvény alakja

Paraméterek értelmezése – grafikus ábrák által Ha 0 b 1, akkor rugalmatlan (lassuló növekedésű) a függvény. A rugalmatlan hatványfüggvény alakja

Paraméterek értelmezése – grafikus ábrák által Ha b 0, akkor csökkenő a függvény. A csökkenő hatványfüggvény alakja

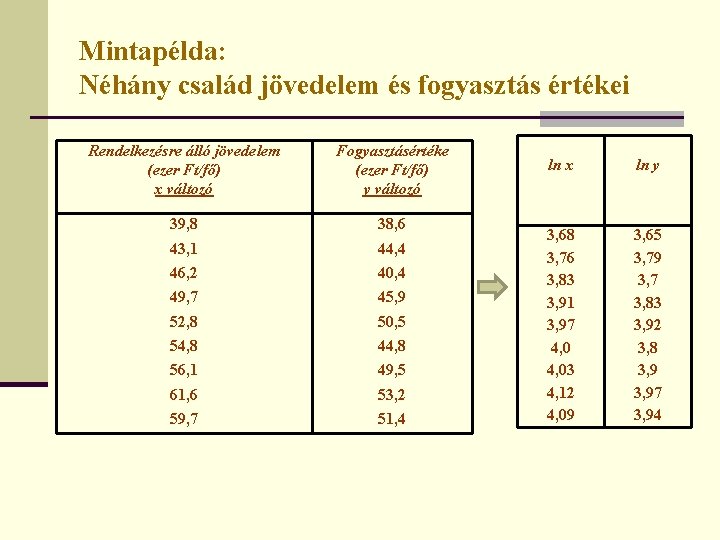
Mintapélda: Néhány család jövedelem és fogyasztás értékei Rendelkezésre álló jövedelem (ezer Ft/fő) x változó Fogyasztásértéke (ezer Ft/fő) y változó 39, 8 38, 6 43, 1 44, 4 46, 2 40, 4 49, 7 45, 9 52, 8 50, 5 54, 8 44, 8 56, 1 49, 5 61, 6 53, 2 59, 7 51, 4 ln x ln y 3, 68 3, 76 3, 83 3, 91 3, 97 4, 03 4, 12 4, 09 3, 65 3, 79 3, 7 3, 83 3, 92 3, 8 3, 97 3, 94

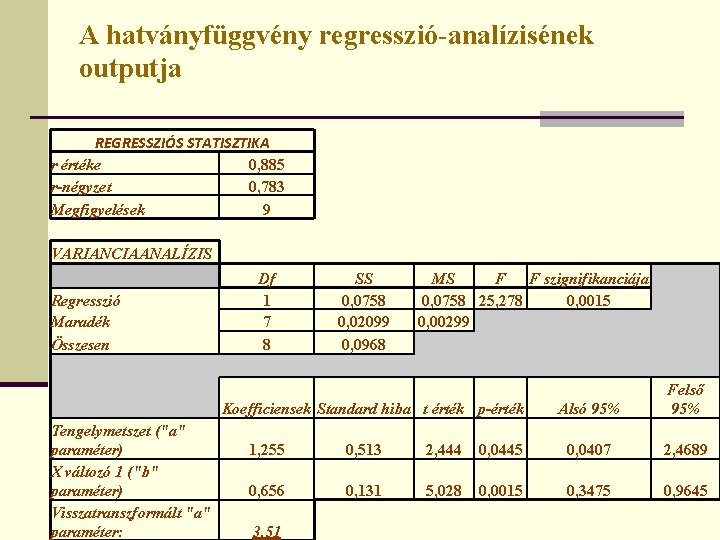
A hatványfüggvény regresszió-analízisének outputja REGRESSZIÓS STATISZTIKA r értéke 0, 885 r-négyzet 0, 783 Megfigyelések 9 VARIANCIAANALÍZIS Regresszió Maradék Összesen Df 1 7 8 SS 0, 0758 0, 02099 0, 0968 MS F F szignifikanciája 0, 0758 25, 278 0, 0015 0, 00299 Koefficiensek Standard hiba t érték p-érték Tengelymetszet ("a" paraméter) X változó 1 ("b" paraméter) Visszatranszformált "a" paraméter: Alsó 95% Felső 95% 1, 255 0, 513 2, 444 0, 0445 0, 0407 2, 4689 0, 656 0, 131 5, 028 0, 0015 0, 3475 0, 9645 3, 51

A táblázat alapján az eredmények értelmezése A regressziós függvény a következő Csak a „b” paramétert értelmezzük, amely azt mutatja meg, hogy a jövedelem 1%-os emelkedése a fogyasztás 0, 656%-os emelkedését vonja maga után. Hatványfüggvény esetén a „b” paramétert rugalmassági (elaszticitási) együtthatónak is hívják

Exponenciális regresszió Ennek a típusnak is van gyakorlati jelentősége, főleg idősorok esetén, amikor azt vizsgáljuk, hogy egyik időszakról a másikra hány százalékkal változott a vizsgált jelenség. Az exponenciális-függvény képlete: Az „a” paramétert a gyakorlatban nem értelmezzük. A „b” paraméter azt mutatja meg, hogy „x” egységnyi változása az „y” hány %-os változását vonja maga után. Az exponenciális függvény lefutása a „b” paraméter értékétől függ.

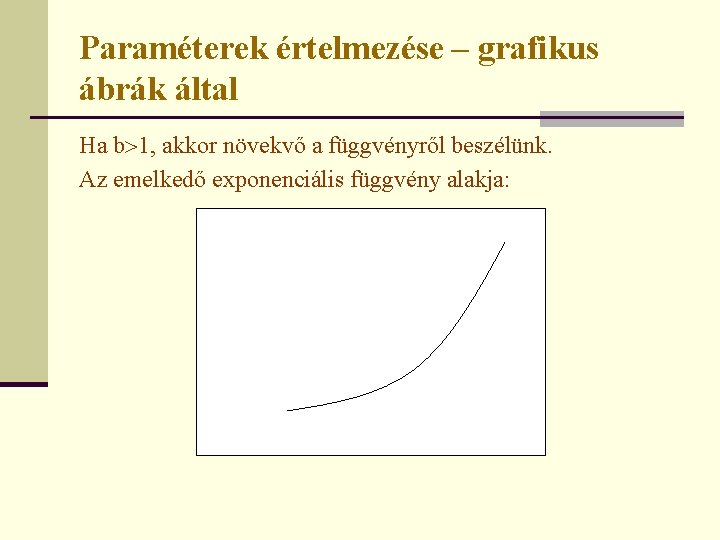
Paraméterek értelmezése – grafikus ábrák által Ha b 1, akkor növekvő a függvényről beszélünk. Az emelkedő exponenciális függvény alakja:

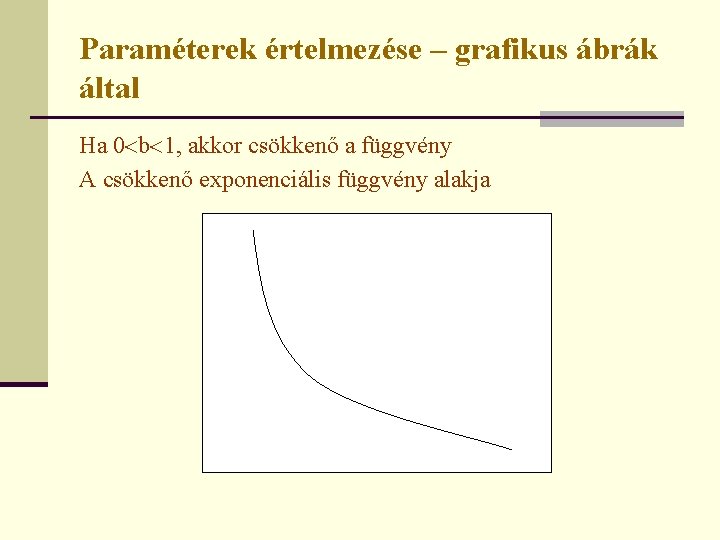
Paraméterek értelmezése – grafikus ábrák által Ha 0 b 1, akkor csökkenő a függvény A csökkenő exponenciális függvény alakja

A függvény átalakítása Az exponenciális függvény is átalakítható lineárissá, logaritmizálás segítségével: Az átalakítás után nem „x”-ek és „y”-ok között van lineáris kapcsolat, hanem log „y”-ek és „x”-ek között, tehát az eredeti „y” változók logaritmusát kell képezni, és log „y”-ok és „x”-ek között keresni a lineáris kapcsolatot.

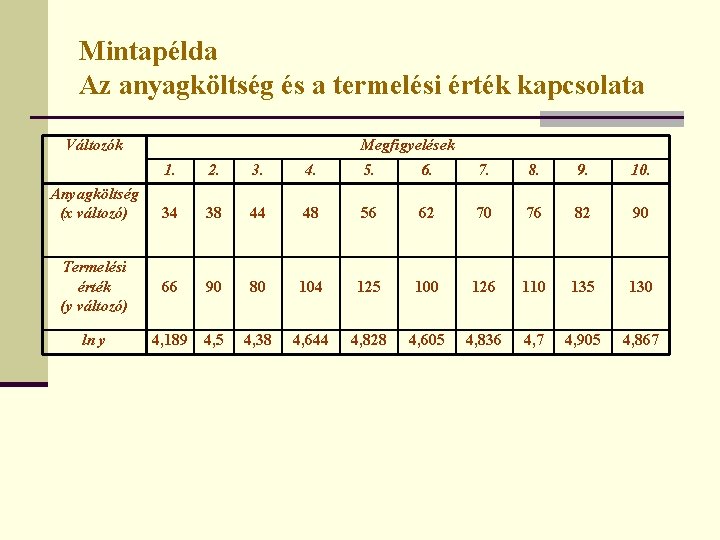
Mintapélda Az anyagköltség és a termelési érték kapcsolata Változók Anyagköltség (x változó) Termelési érték (y változó) ln y Megfigyelések 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 34 38 44 48 56 62 70 76 82 90 66 90 80 104 125 100 126 110 135 130 4, 38 4, 644 4, 828 4, 605 4, 836 4, 7 4, 905 4, 867 4, 189 4, 5

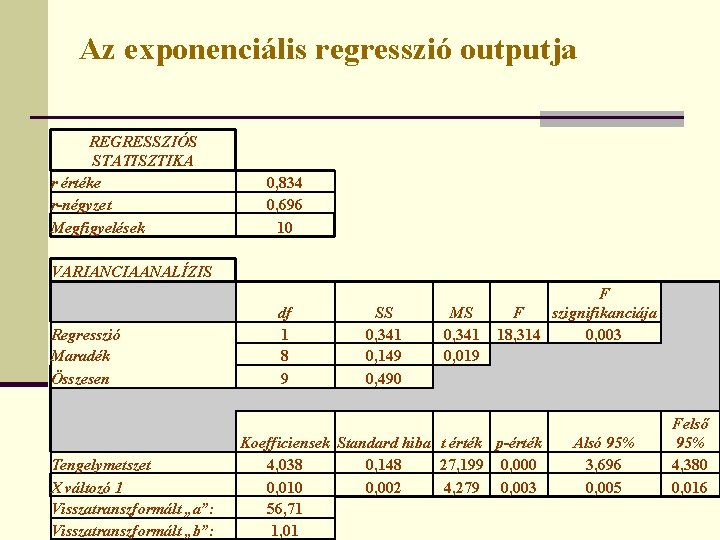
Az exponenciális regresszió outputja REGRESSZIÓS STATISZTIKA r értéke r-négyzet Megfigyelések 0, 834 0, 696 10 VARIANCIAANALÍZIS Regresszió Maradék Összesen Tengelymetszet X változó 1 Visszatranszformált „a”: Visszatranszformált „b”: df 1 8 9 SS 0, 341 0, 149 0, 490 MS 0, 341 0, 019 F F szignifikanciája 18, 314 0, 003 Koefficiensek Standard hiba t érték p-érték 4, 038 0, 148 27, 199 0, 000 0, 010 0, 002 4, 279 0, 003 56, 71 1, 01 Alsó 95% 3, 696 0, 005 Felső 95% 4, 380 0, 016

A táblázat alapján az eredmények értelmezése A függvény képlete a következő: Az „a” paramétert nem értelmezzük. A „b” paraméter azt mutatja meg, hogy ha egységgel nő az „x”, akkor az „y”, b. 100 százalékra változik. Konkrétan a mi példánkban, ha az anyagköltség 1000 Ft-tal emelkedik, akkor a termelési érték 1%-kal (101 %-ra) nő.

Köszönöm a figyelmet