Kvantitatv mdszerek 4 Korrelci s regressziszmts I Dr

Kvantitatív módszerek 4. Korreláció- és regressziószámítás I. Dr. Kövesi János egyetemi tanár

Determinisztikus és sztochasztikus kapcsolatok n n 44 A korreláció- és regresszió- számítás során arra keressük a választ, hogy egy adott állapot milyen tényezők hatására jött létre, az egyes tényezők milyen mértékben befolyásolják a jelenség alakulását, a tényezők milyen szoros kapcsolatban vannak egymással. A korrelációs és regressziós számítás a kapcsolatot jellemzi, de semmit nem mond az oksági viszonyról. Tehát két, vagy több változó közötti sztochasztikus kapcsolat megállapításából nem következik, hogy a változók oksági összefüggésben vannak, azaz, hogy egyik tényező változása oka a másik tényező változásának. Az oksági kapcsolatot csak alapos szakmai és statisztikai vizsgálattal lehet megállapítani.

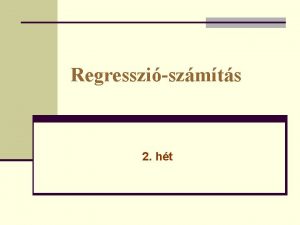
45 A kapcsolat szemléltetése 3 2 1 3 3 40 Y=-8. 6 E-02+0. 690286 X Y = 5. 07 E-02 - 0. 647872 X 3 Y = -7 Y. 4=E-8. 6 E -0 2 -02 + 0 Y+. 20. 6902 0=8 35 4. 0 88 X R-Sq=62. 5% 76 X E - 0 2 - 0. 6 4 7 8 R-Sq 7 2=X 70. 9 % Y = 1 2. 0 9 5 8 + 6. 0 7 6 8 4 X + 1. 1 6 6 8 6 X* * 2 2 R - S q = 3. R-Sq 4 % = 6 2. 5 % 3 R -S q = 7 0. 9 % R -S q = 8 8. 4 % 1 0 2 2 -1 -2 -1 30 -2 1 1 1 -3 -3 -3 -2 -1 0 0 0 -1 3 2 2 3 Pozitív korreláció -3 -1 Y = -7. 4 E-02 -+1 0. 208348 X R-Sq = 3. 4 % 0 1 Negatív korreláció 2 3 Y = 12. 0958 + 6. 07684 X+ 1. 16686 X**2 R-Sq = 88. 4 % 40 10 -2 -2 1 30 -2 0 20 -3 -1 -2 0 20 -1 1 -3 0 -3 10 -2 -2 -3 -3 -2 -1 -1 -2 -1 -3 -1 0 0 -2 0 1 -1 1 1 2 0 2 2 3 1 3 2 N i n c s k o r r e lá c i ó N e m li n e á r i s k P o ror ze ilá t ívc ki óo. Nr er egláa 0 ct iívó k o r r e lá c i ó -3 -2 -1 0 1 2 Nem lineáris korreláció Nincs korreláció 3 2 3

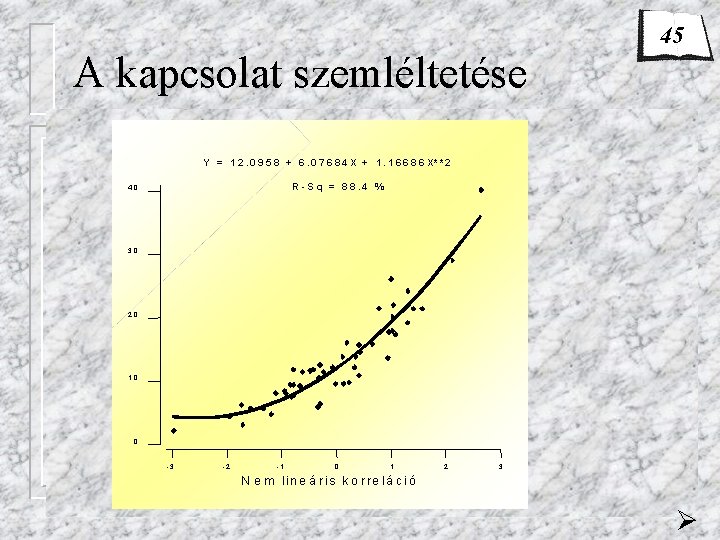
46 -47 Az előjel–korrelációs együttható Feladat: 14 év adatai alapján vizsgáljuk meg az 1 ha szántóterületre vonatkoztatott műtrágya felhasználás (xi=kg/ha) és az évi búza termés átlagok (yi=q/ha) közötti kapcsolatok jellegét és szorosságát. 12 - 2 = 0, 71 re = 14

A (lineáris) regresszió és korreláció 48 A regresszió számítás feladata a változók közötti összefüggés jellegének meghatározása. Ennek során a pontdiagramos ábrázolással érzékeltetett tendenciát valamilyen analitikusan ismert függvénnyel próbáljuk leírni. A regressziós függvényt a legkisebb négyzetek elve és módszere alapján határozzuk meg. Ez azt a követelményt támasztja, hogy az adott függvénytípust (egyenes, parabola, exponenciális, stb. ) használata során a összeg minimális legyen. Az eltérések (rezidiumok) négyzeteinek összege jól jellemzi a ponthalmaz és a regressziós vonal kölcsönös viszonyát.

A (lineáris) regresszió és korreláció 51 A korrelációs együttható értéke nulla, ha X és Y függetlenek. Ez fordítva általában nem igaz: abból, hogy két valószínűségi változó korrelációs együtthatója nulla, nem feltétlenül következik, hogy a két változó független is egymástól (kivétel, ha X és Y együttes eloszlása normális). Ha a két változónál csak azt tudjuk, hogy r(x, y)=0, akkor korrelálatlannak nevezzük őket.

A (lineáris) korrelációs együttható 51 Az elméleti korrelációs együtthatót a mintabeli, tapasztalati korrelációs együtthatóból becsülhetjük: ahol: és

52 Feladat: Számítsuk ki a mintapéldában szereplő változó korrelációs együtthatóját! Emlékeztetőül: az előjel – korrelációs együttható értéke 0, 71 volt.

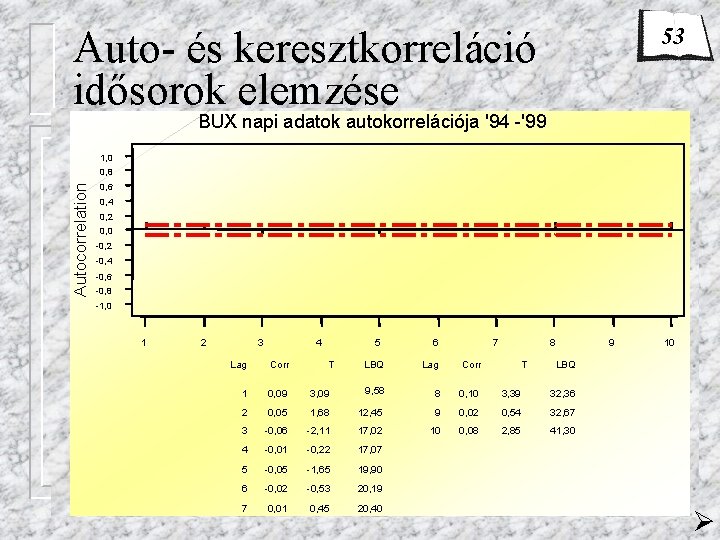
53 Auto- és keresztkorreláció idősorok elemzése BUX napi adatok autokorrelációja '94 -'99 1, 0 Autocorrelation 0, 8 0, 6 0, 4 0, 2 0, 0 -0, 2 -0, 4 -0, 6 -0, 8 -1, 0 1 2 3 4 T 5 6 7 LBQ Lag Corr 8 Lag Corr T 1 0, 09 3, 09 9, 58 8 0, 10 3, 39 32, 36 2 0, 05 1, 68 12, 45 9 0, 02 0, 54 32, 67 3 -0, 06 -2, 11 17, 02 10 0, 08 2, 85 41, 30 4 -0, 01 -0, 22 17, 07 5 -0, 05 -1, 65 19, 90 6 -0, 02 -0, 53 20, 19 7 0, 01 0, 45 20, 40 9 10 LBQ

Kvantitatív módszerek 11. Korreláció- és regressziószámítás II. Dr. Kövesi János

A (lineáris) korrelációs együttható 128 A korrelációs együttható értéke nulla, ha X és Y függetlenek. Ez fordítva általában nem igaz: abból, hogy két valószínűségi változó korrelációs együtthatója nulla, nem feltétlenül következik, hogy a két változó független is egymástól (kivétel, ha X és Y együttes eloszlása normális). Ha a két változónál csak azt tudjuk, hogy R(X, Y)=0, akkor korrelálatlannak nevezzük őket.

A (lineáris) korrelációs együttható 129 Az elméleti korrelációs együtthatót a mintabeli, tapasztalati korrelációs együtthatóból becsülhetjük: ahol: és

129 A (lineáris) korrelációs együttható szignifikancia vizsgálata Ho: R (X, Y) = 0 A két változó egymástól független normális eloszlású Ha H 0 igaz, akkor r(x, y) alábbi függvénye DF=n-2 szabadság fokkal t - eloszlást követ: Ha adott mellett tsz>tkrit, akkor H 0 -t elvetjük és =1 - megbízhatósággal állíthatjuk, hogy a két változó között sztochasztikus kapcsolat áll fenn.

A (lineáris) korrelációs együttható 129 Feladat: Számítsuk ki a mintapéldában szereplő változó korrelációs együtthatóját és végezzük el a szignifikancia vizsgálatot! Ho: R (X, Y) = 0 DF= n-2 =14 -2 = 12 =0, 05 tkrit = 2, 17 Mivel tsz tkrit, ezért a nullhipotézist elvetjük és nagy biztonsággal állíthatjuk, hogy a két változó között korrelációs (sztochasztikus) kapcsolat van. (Emlékeztetőül: az előjel – korrelációs együttható értéke 0, 71 volt).

130 Az r(x, y) és a regressziós egyenes összefüggése Az r 2 (x, y) – amelyet determinációs együtthatónak is neveznek – azt fejezi ki, hogy a sztochasztikus kapcsolatban a teljes változás hányad része tulajdonítható x-nek. Értékét %-os formában is megadhatjuk.

Feladat 130 A mintapélda adatai alapján határozzuk meg a determinációs index értékét! Az eredményt úgy értelmezhetjük, hogy a termésátlagok változásában a műtrágya felhasználás 72%-ban játszott szerepet.

131 A regressziós becslés pontossága Nyilvánvaló, hogy a sztochasztikus kapcsolat mérőszámaiból csak akkor vonhatunk le helyes következtetéseket, ha megfelelően nagy mintánk van. Így, az eredmények értékeléséhez hozzátartozik a mérőszámok hibájának vizsgálata is. A pontosság jellemzése céljából tehát most az a, b, paraméterek becslésének szórását (standard hibáját) kell meghatároznunk: 1. A regressziós együtthatók standard hibái (pontbecslés). 2. Konfidencia intervalluma becsült paraméterekre. 3. A lineáris kapcsolat szignifikancia vizsgálata. 4. Az átlagos, vagy az egyedi yi értékek becslése.

1. A regressziós együtthatók standard hibái (pontbecslés). 131 A standard hibák azt mutatják meg, hogy végtelen sok n elemű mintát véve az alapsokaságból az egyes mintákból becsült b 0 és b 1 paraméterek átlagosan sb 0 és sb 1 egységgel szóródnak az alapsokasági regressziófüggvény körül.

2. Konfidencia intervallum a becsült paraméterekre 131 A becsült paraméterekre konfidencia intervallumokat is konstruálhatunk. Nagy minták esetén normális eloszlás táblázatot-, kis minták esetén a Student-eloszlás t- táblázatát használjuk (DF= n-2):

3. A lineáris kapcsolat szignifikancia vizsgálata 132 t- próba segítségével azt is ellenőrizhetjük, hogy az Y és X változók között szignifikáns lineáris kapcsolat van-e. Nullhipotézisünk és ellenhipotézisünk: A próbastatisztika: A tkrit értéket szignifikancia szinten DF=n – 2 szabadsági foknál találjuk meg. Ha tsz tkrit, elvetjük Ho-t és valós lineáris összefüggést tételezünk fel X és Y között.

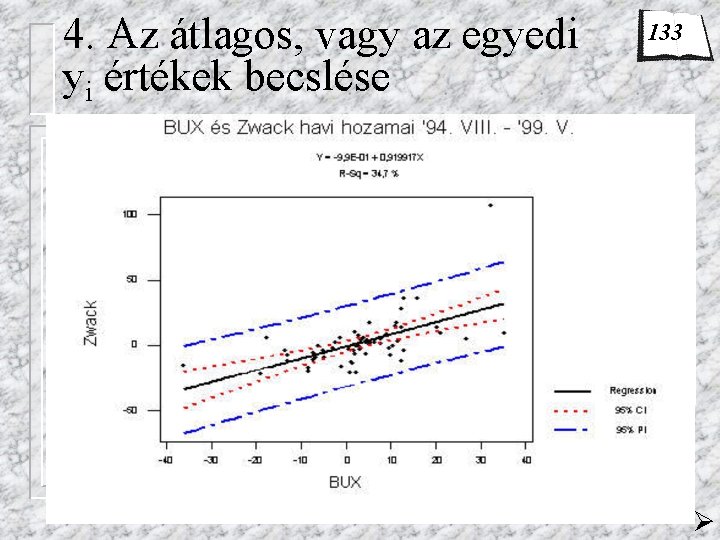
4. Az átlagos, vagy az egyedi yi értékek becslése 133

Feladat 134 Korábban már többször foglalkoztunk a BUX havi hozamainak statisztikai elemzésével (leíró statisztika, hipotézisvizsgálatok). Az alábbi táblázat alapján vizsgáljuk meg, hogy az 1998. VII. -1999. VI. közötti időszakban a havi hozam (%) alapján kimutatható-e sztochasztikus kapcsolat a BUX és a Zwack hozamai között? Adjunk – előzetes – szakmai magyarázatot az eredményekre!

143 5 Feladat A diagram és/vagy a táblázat alapján határozzuk meg az előjel – korrelációs együtthatót! Határozzuk meg a tapasztalati korrelációs együtthatót és = 5 % mellett végezzük el a szignifikancia vizsgálatot! Következtetés: tsz > tkrit Ho: R(x, y) = 0 DF = 12 -2 = 10 = 5% tkrit = 2, 23 H 0 nem igaz !

Feladat 135 Becsüljük meg a lineáris regressziófüggvény együtthatóit! Határozzuk meg a determinációs együtthatót és értelmezzük az eredményt! Következtetés: A Zwack hozamának változásában a BUX hozama 46, 2 %-ban játszott szerepet.

136 Feladat Határozzuk meg a regressziós becslés pontosságát! se = 7, 47 sb 0 = 2, 157 sb 1 = 0, 143 Készítsünk 95 %-os konfidencia intervallumot a becsült paraméterekre! = 5% t a = 2, 23 Int(1 -α)(βo) = 1, 47 4, 841 1 Int(1 -α)(β 1) = 0, 463 0, 32 2 Ellenőrizzük = 5 % mellett, hogy a lineáris kapcsolat szginifikáns-e? DF = 10 tsz = 3, 24 tkrit = 2, 23 Következtetés: Mivel tsz >tkrit a H 0 (β 1=0) nem igaz, tehát x és y között szignifikáns lineáris kapcsolat van.