Quicksort A Case Study in Randomization and AverageCase


![Idea To sort the subrange v[p]…v[r]: • let a = v[p]; a is called Idea To sort the subrange v[p]…v[r]: • let a = v[p]; a is called](https://slidetodoc.com/presentation_image/941f454e70c2d058108160a20b5a52fe/image-4.jpg)




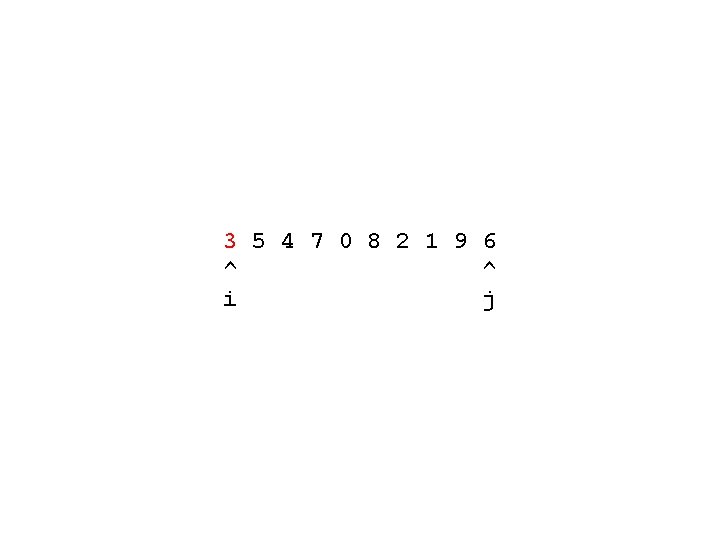

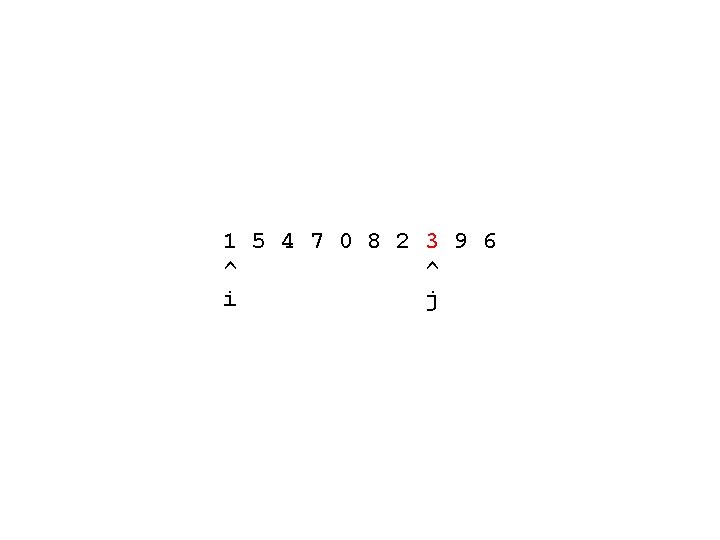
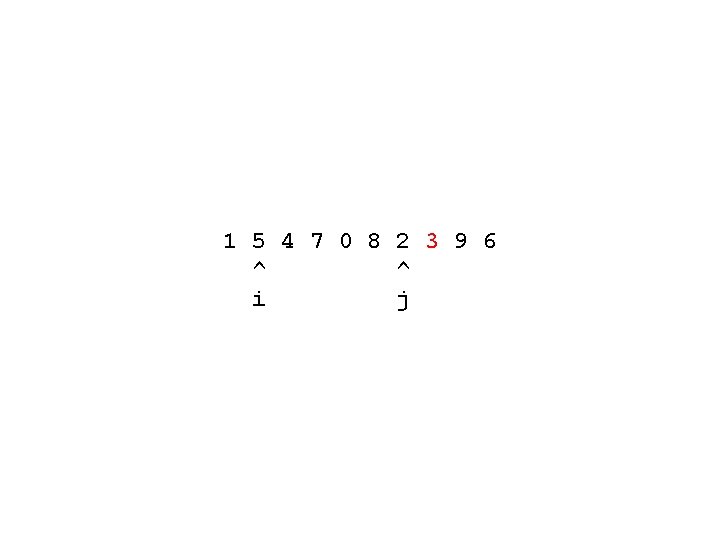
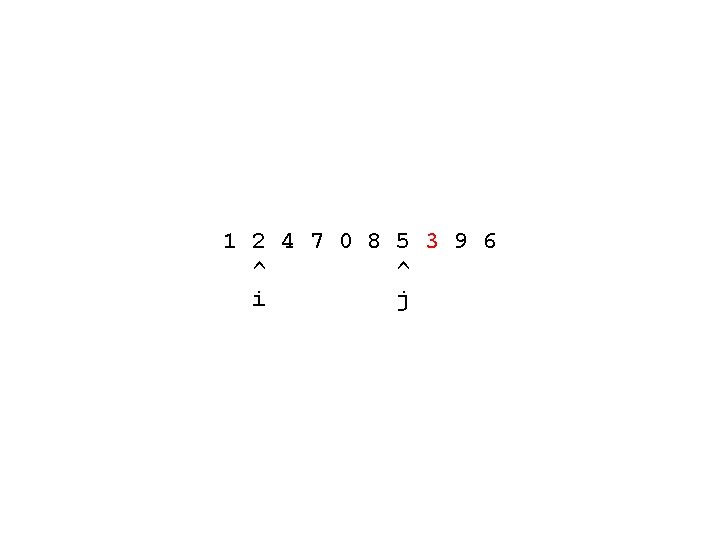


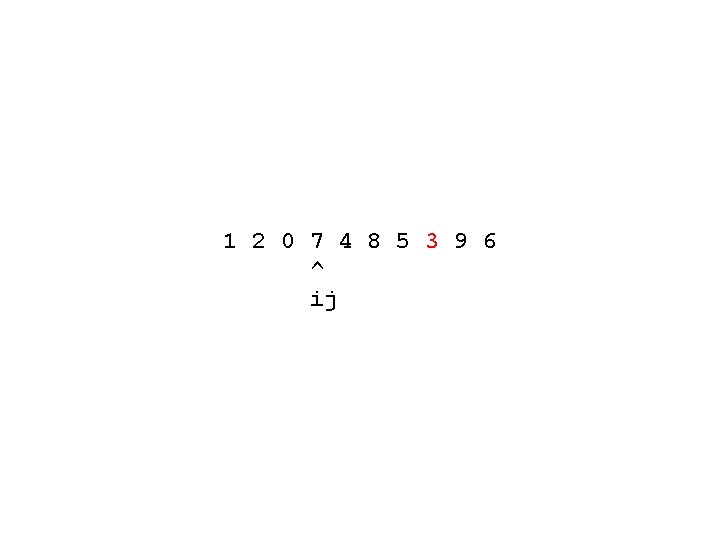


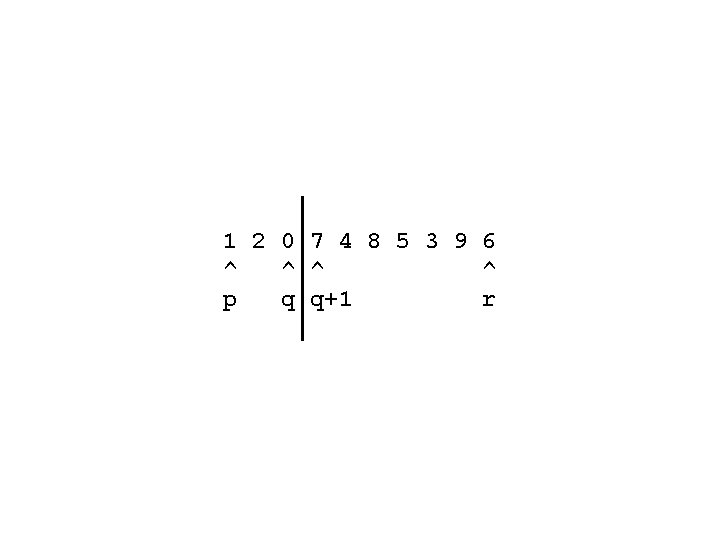







- Slides: 28

Quicksort A Case Study in Randomization and Average-Case Complexity Bubblesort O(n 2) Mergesort O(n log n) Heapsort O(n log n) worst case

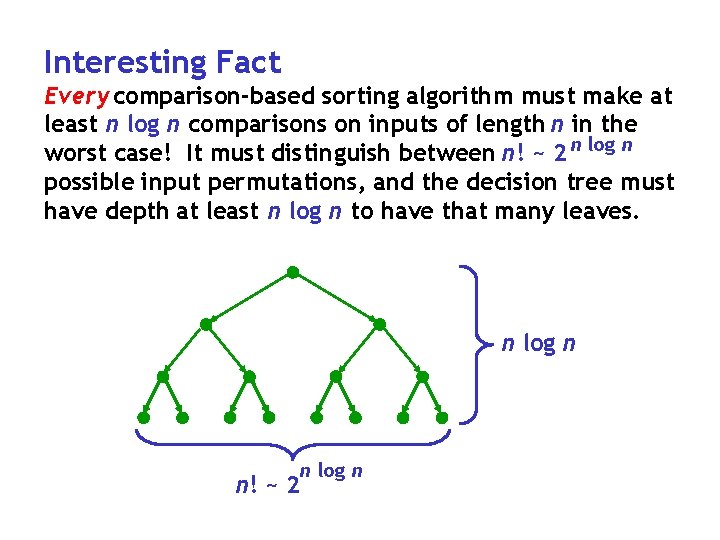
Interesting Fact Every comparison-based sorting algorithm must make at least n log n comparisons on inputs of length n in the worst case! It must distinguish between n! ~ 2 n log n possible input permutations, and the decision tree must have depth at least n log n to have that many leaves. n log n n! ~ 2

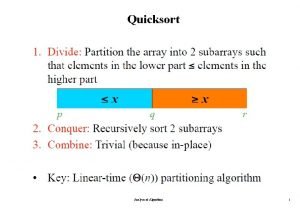
QUICKSORT—a very fast sorting method • Worst case O(n 2 ); so what's so quick about it? • It's O(n log n) expected time • It's got a very small constant
![Idea To sort the subrange vpvr let a vp a is called Idea To sort the subrange v[p]…v[r]: • let a = v[p]; a is called](https://slidetodoc.com/presentation_image/941f454e70c2d058108160a20b5a52fe/image-4.jpg)
Idea To sort the subrange v[p]…v[r]: • let a = v[p]; a is called the pivot • move elements a to the front • move elements a to the back • let q be such that all v[p]…v[q] a and all v[q+1]…v[r] a; recursively sort v[p]…v[q] and v[q+1]…v[r]

; ; sort the subrange of vector v ; ; from p to r, inclusive (define (qsort! <function>) (method ((v <vector>) (p <integer>) (r <integer>)) (when (< p r) (bind (((q <integer>) (partition! v p r))) (qsort! v p q) (qsort! v (inc q) r)))))

; ; move small elements to beginning of interval ; ; large elements to end of interval ; ; return max bound of lower subinterval (define (partition! <function>) (method ((v <vector>) (p <integer>) (r <integer>)) (bind (((pivot <number>) (index v p))) (bind-methods ((count-down ((k <integer>)) (if (<= (index v k) pivot) k (count-down (dec k)))) (count-up ((k <integer>)) (if (>= (index v k) pivot) k (count-up (inc k)))) (iter ((i <integer>) (j <integer>)) (cond ((< i j) (swap! v i j) (iter (count-up (inc i)) (count-down (dec j)))) (else: j)))) (iter (count-up p) (count-down r))))))

; ; swap two elements of an array in place (define (swap! <function>) (method ((v <vector>) (i <integer>) (j <integer>)) (bind (((temp <number>) (index v i))) (index-setter! i v (index v j)) (index-setter! j v temp))))

3 5 4 7 0 8 2 1 9 6 ^ ^ p r
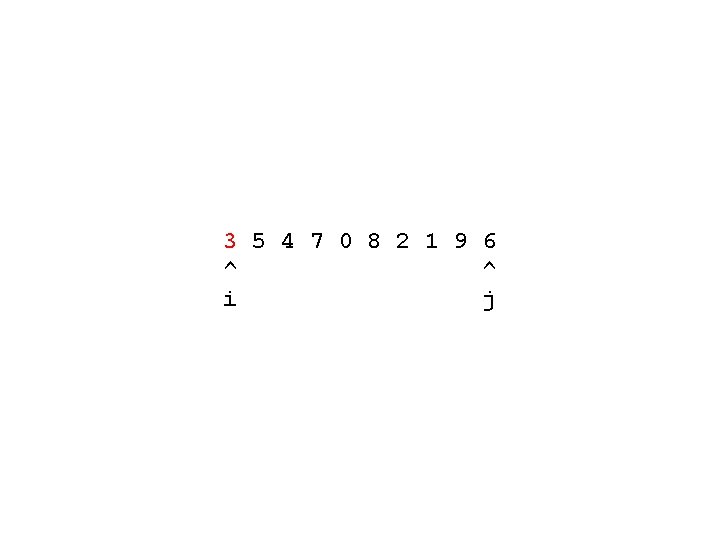
3 5 4 7 0 8 2 1 9 6 ^ ^ i j

3 5 4 7 0 8 2 1 9 6 ^ ^ i j
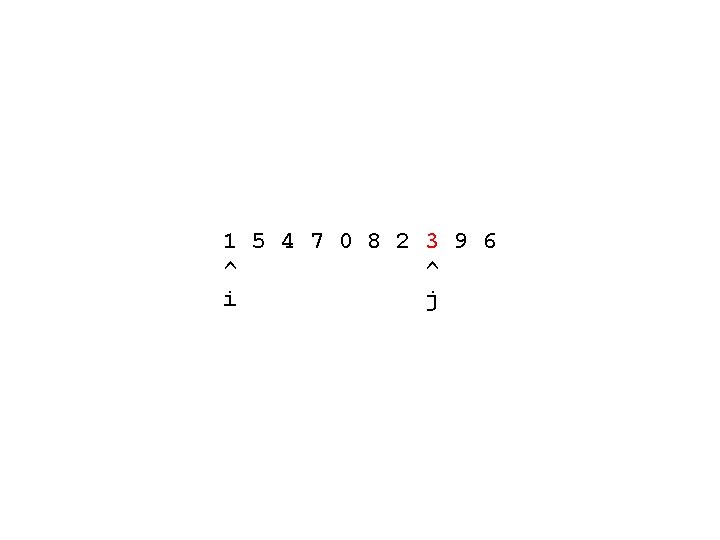
1 5 4 7 0 8 2 3 9 6 ^ ^ i j
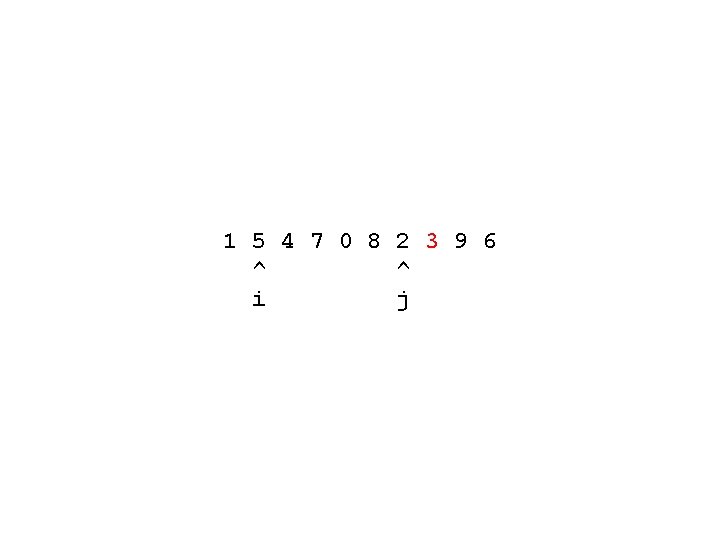
1 5 4 7 0 8 2 3 9 6 ^ ^ i j
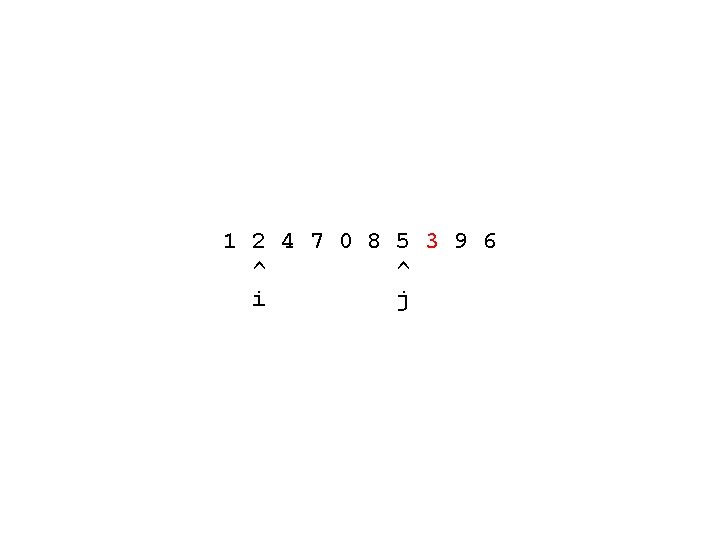
1 2 4 7 0 8 5 3 9 6 ^ ^ i j

1 2 4 7 0 8 5 3 9 6 ^ ^ i j

1 2 0 7 4 8 5 3 9 6 ^ ^ i j
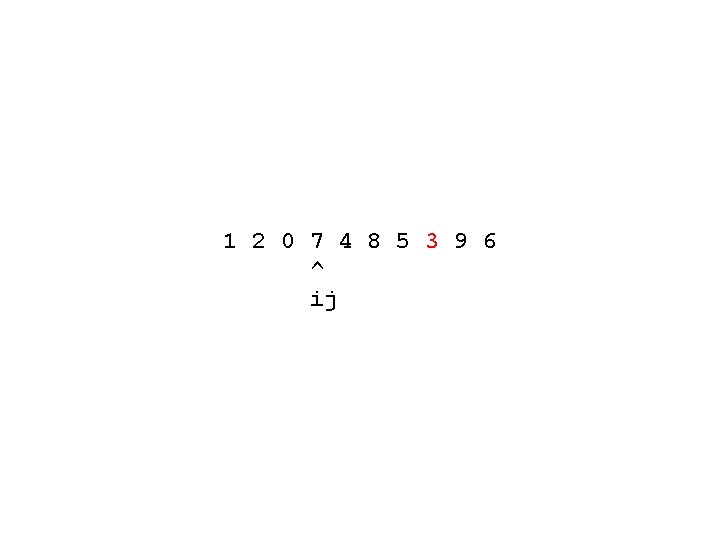
1 2 0 7 4 8 5 3 9 6 ^ ij

1 2 0 7 4 8 5 3 9 6 ^ ^ j i

1 2 0 7 4 8 5 3 9 6 ^ ^ j j+1
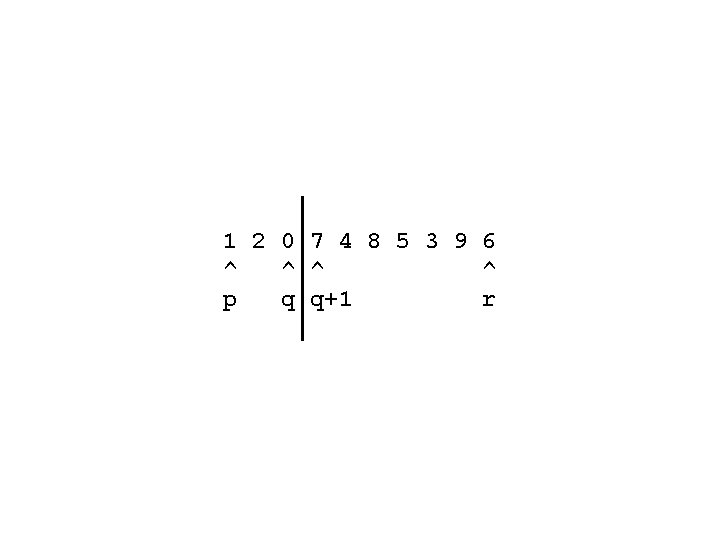
1 2 0 7 4 8 5 3 9 6 ^ ^ p q q+1 r

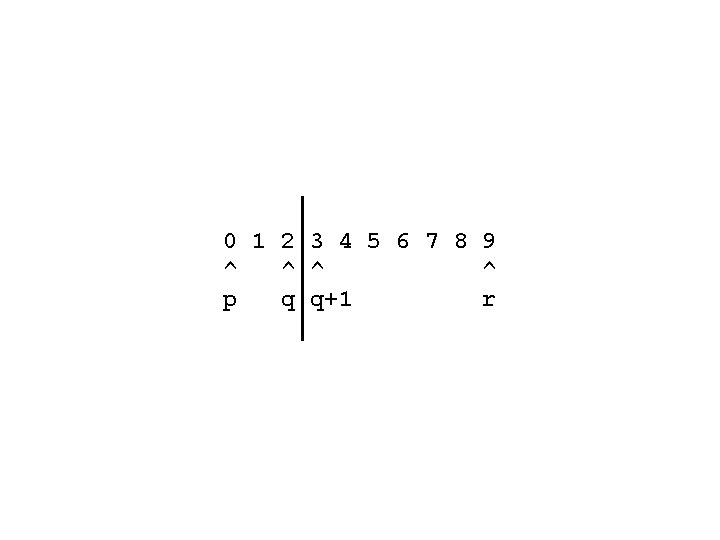
0 1 2 3 4 5 6 7 8 9 ^ ^ p q q+1 r

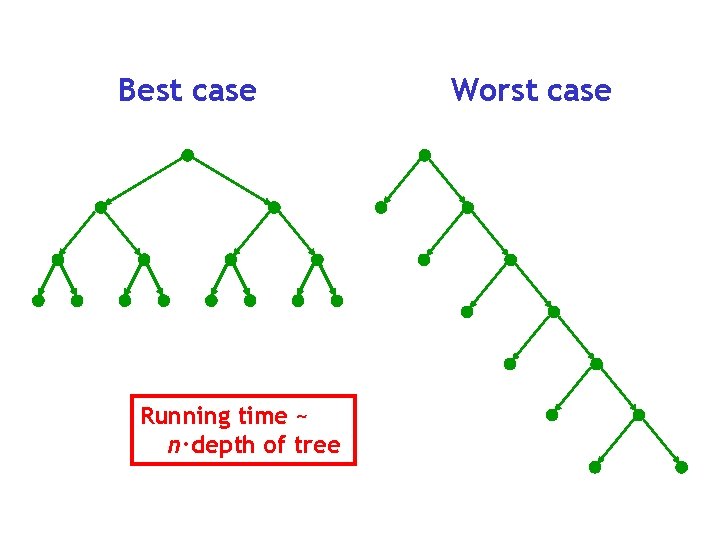
Running time depends on how balanced the partitions are BEST CASE • pivot is always the median of the interval • we cut the array in half in each iteration • T(n) = O(n) + 2 T(n/2) = O(n log n) WORST CASE • pivot is always the smallest element of the interval • gives a 1: n-1 split (example: [1, 2, 3, 4, 5]). • T(n) = T(n-1) + O(n) = O(n^2)

Best case Running time ~ n·depth of tree Worst case

Suppose the partition produces a 9: 1 split 90% in one half, 10% in the other. Still O(n log n) ! T(n) = T(0. 9 n) + T(0. 1 n) + O(n) = O(n log n)

Quicksort will occasionally have bad partitionings at some stages, but it's very unlikely to have enough of them to matter. It can be shown that, if we assume the input is random and uniformly distributed(all permutations equally likely), then the probability that the partition is better than a: 1 -a is 1 -2 a (0 < a 1/2). For example, if we want a 9: 1 or better split, then we compute: • a=0. 1 • probability = 1 -2(0. 1) = 80%

So we would expect about 4 out of every 5 arrays to be 9: 1 or better. Even if the other arrays are utterly useless, this is still exponential decay, and we still get O(n log n).

DEFINITION The expected running time of an algorithm is a function of n giving the average running time on inputs of length n. E(n) = T(x)· Prn(x) |x|= n T(x) = running time on input x Prn(x) = probability that x occurs among inputs of length n THEOREM Assuming the elements of the input vector are distinct and all permutations are equally likely, the expected running time of quicksort is O(n log n).

Q. How reasonable is it to assume the input is random? A. Not very. • worst case = input is already sorted • choosing v[p] as pivot guarantees a 1: n-1 split • this happens a lot in real life

Trick: scramble the input! ; ; scramble a vector (define (scramble! <function>) (method ((v <vector>)) (bind-methods ((scram! ((i <integer>)) (cond ((< i (length v)) (swap! v i (random i)) (scram! (inc i)))))) (scram! 0))))
 Worst case quicksort
Worst case quicksort Best worst and average case
Best worst and average case Project failure case study
Project failure case study Interactive voice response system randomization
Interactive voice response system randomization Stratified randomization
Stratified randomization Randomization module redcap
Randomization module redcap Poonam naik
Poonam naik Stratified randomization
Stratified randomization Randomize questions qualtrics
Randomize questions qualtrics Block randomization example
Block randomization example Types of randomization
Types of randomization Randomization based on remainder
Randomization based on remainder Redcap upenn
Redcap upenn Unit of randomization
Unit of randomization Address space layout randomization
Address space layout randomization Forced randomization
Forced randomization Blocked random assignment
Blocked random assignment Loop invariant quicksort
Loop invariant quicksort Why is merge sort n log n
Why is merge sort n log n Naive quicksort
Naive quicksort Algoritmo quicksort
Algoritmo quicksort Quicksort spiegazione
Quicksort spiegazione Linked list quicksort
Linked list quicksort Heap sort worst case time complexity
Heap sort worst case time complexity Quicksort recursive
Quicksort recursive Recursivo
Recursivo Sortieralgorithmen java quicksort
Sortieralgorithmen java quicksort Parallel quicksort
Parallel quicksort Quicksort java arreglos
Quicksort java arreglos