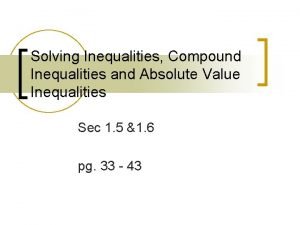Quantum Entanglement and Bells Inequalities Kristin M Beck

Quantum Entanglement and Bell’s Inequalities Kristin M. Beck and Jacob E. Mainzer Demonstrating quantum entanglement of photons via the violation of Bell’s Inequality

Outline n Relevant Physics Concepts n Experimental Setup and Procedure n Relationship between Setup and Physical Concepts n Results n Conclusions

Physical Concepts Quantum Entanglement between two particles n Particles’ wave functions cannot be separated n Measurement of one particle affects the state of the other n No classical model of this behavior n In this lab, polarization states of two photons were entangled

Physical Concepts Bell’s Inequality n Classical relationship n Used to discern quantum effects from classical effects n In this lab, violation of a Bell’s Inequality is used to show no hidden variables (EPR paradox)
D AP Beam Stop AP D Experimental Setup BBO crystals Quartz Plate Laser Mirror Blue Filter

Experimental Setup Laser Quartz Plate Mirror BBO Crystals

Experimental Setup Interference Filters Beam Stop APD Polarizers
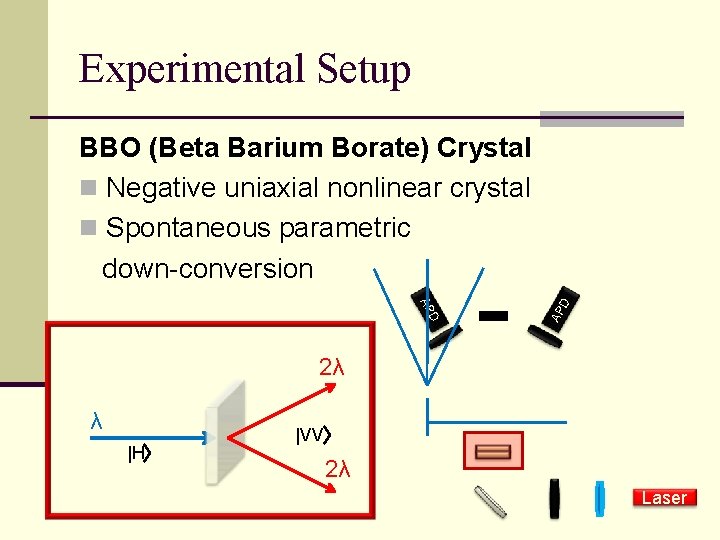
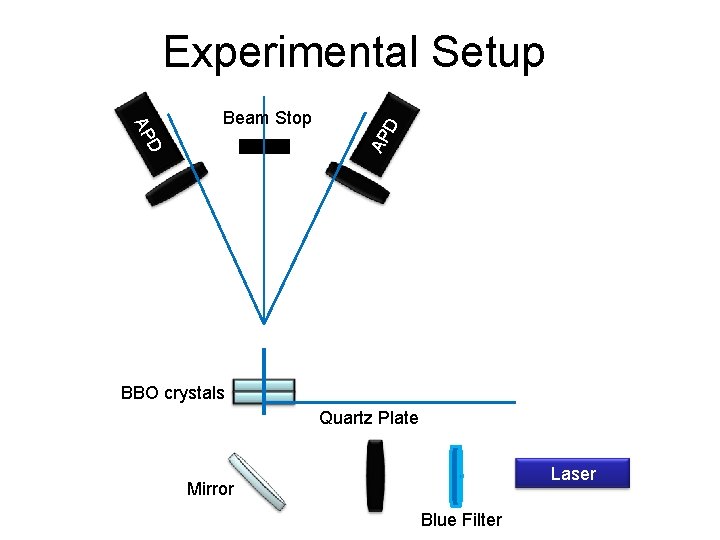
Experimental Setup D AP AP D BBO (Beta Barium Borate) Crystal n Negative uniaxial nonlinear crystal n Spontaneous parametric down-conversion 2λ λ |H |VV 2λ Laser

Video (Click to Play) Downconverted Light Cone from 2 mm thick BBO Type I crystal
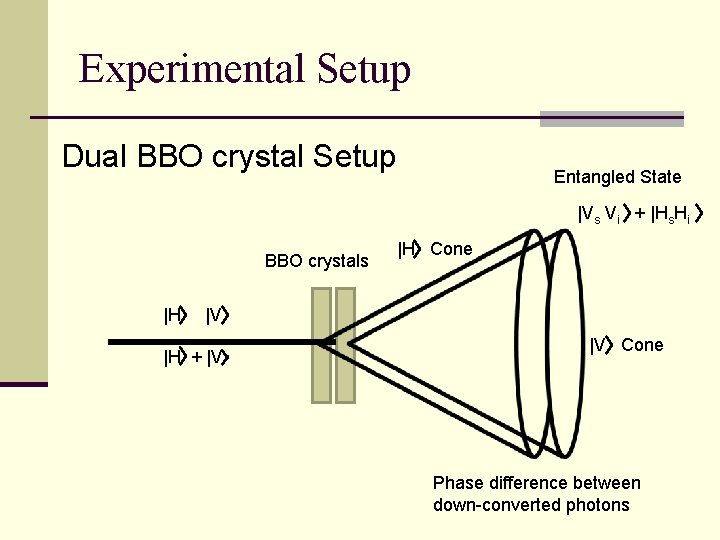
Experimental Setup Dual BBO crystal Setup Entangled State |Vs Vi + |Hs. Hi BBO crystals |H |H Cone |V |H + |V |V Cone Phase difference between down-converted photons
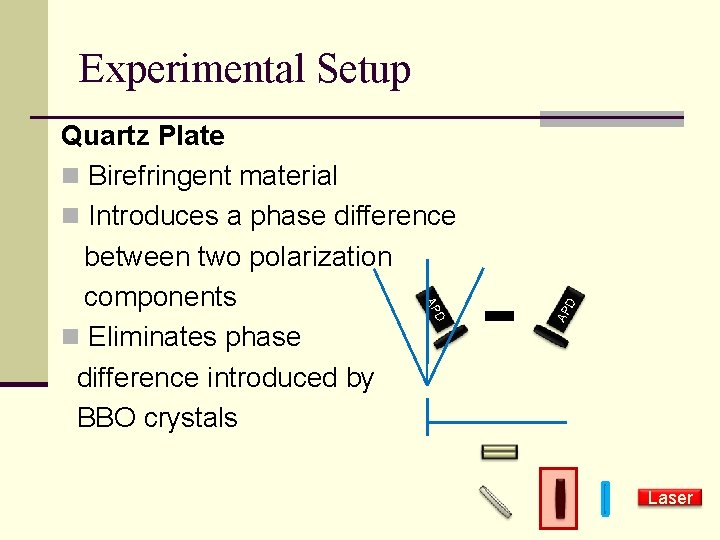
AP D AP Quartz Plate n Birefringent material n Introduces a phase difference between two polarization components n Eliminates phase difference introduced by BBO crystals D Experimental Setup Laser

D AP Polarizers n Select a particular polarization state n Block other photon polarizations n Used to measure photon polarization with APDs AP D Experimental Setup Laser

AP D AP APDs n Single-photon counting avalanche photodiodes n Dual APDs record coincidence photon count (26 ns) n Perkin. Elmer SPCM-AQR D Experimental Setup Laser

How does our setup relate to the key physical concepts? What we expect to observe by moving the polarizers n Coincidence count related to polarizer angles α and β by cos 2(α – β) because of entanglement n Measurement at one polarizer affects measurement at the other polarizer n A 0 o-90 o polarizer setup should yield a minimum coincidence count
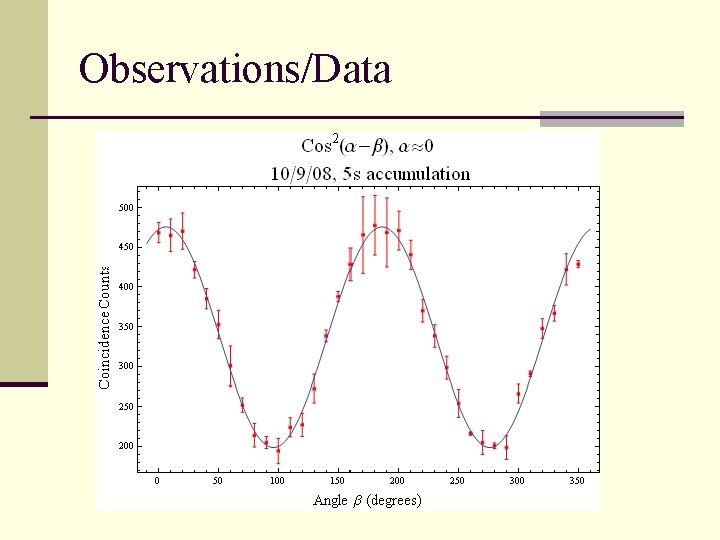
Observations/Data
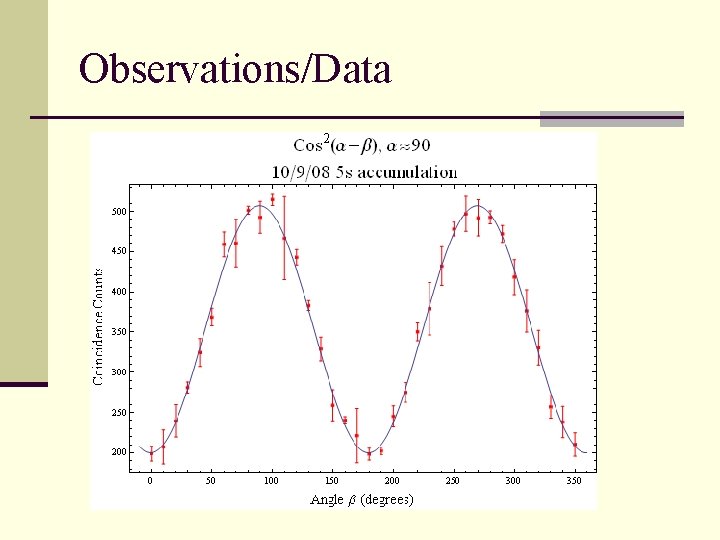
Observations/Data

How does our setup relate to the key physical concepts? Application of Bell’s Inequality n Calculating S, average polarization correlation between pairs of particles n Classically, by Bell’s Inequality, |S| ≤ 2 n |S| > 2 evidence for quantum entanglement n Calculated by measuring coincidence counts (N) for various polarizer angles
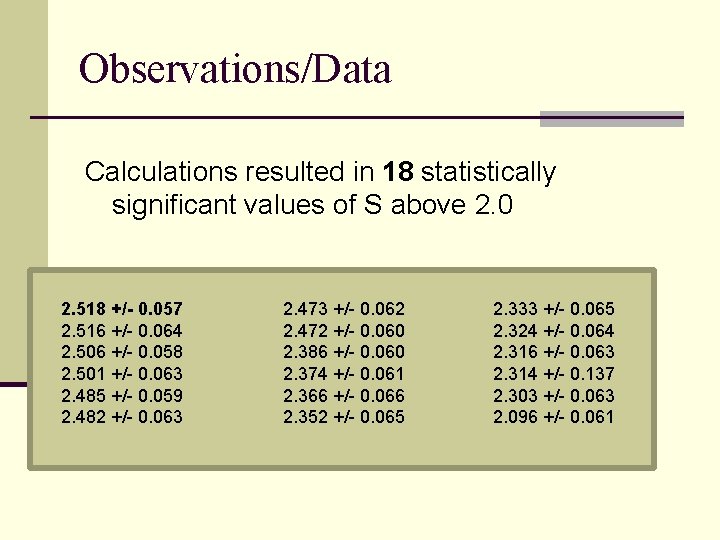
Observations/Data Calculations resulted in 18 statistically significant values of S above 2. 0 2. 518 +/- 0. 057 2. 516 +/- 0. 064 2. 506 +/- 0. 058 2. 501 +/- 0. 063 2. 485 +/- 0. 059 2. 482 +/- 0. 063 2. 473 +/- 0. 062 2. 472 +/- 0. 060 2. 386 +/- 0. 060 2. 374 +/- 0. 061 2. 366 +/- 0. 066 2. 352 +/- 0. 065 2. 333 +/- 0. 065 2. 324 +/- 0. 064 2. 316 +/- 0. 063 2. 314 +/- 0. 137 2. 303 +/- 0. 063 2. 096 +/- 0. 061

Error n Our calculation for σS is: n Sources of experimental error : (1) Errors in aligning polarizers, each 1 degree of error (2) accidental coincidences (Nacc = t. Na. Nb/Tmeasure) 10/9/08 : : 14. 47813 Tmeasure = 1 s 10/14/08 : : 76. 66656 Tmeasure = 5 s 10/16/08 : : 91. 93551 Tmeasure = 5 s (3) human error in selecting the proper counts to record

Conclusion n Quantum entanglement was demonstrated by a cos 2(α – β) coincidence count dependence n Additionally, we verified quantum behavior by calculating Bell’s Inequality and showing that it violated the classical limit |S| ≤ 2

References D. Dehlinger and M. W. Mitchell, “ Entangled photons, nonlocality, and Bell inequalities in the undergraduate laboratory”, Am. J. Phys, 70, 903 (2002). J. Eberly, “Bell inequalities and quantum mechanics”, Amer. J. Phys. , 70 (3), 286, March (2002). S. Lukishova. 2008. Entanglement and Bell’s Inequalities. OPT 253. University of Rochester, NY.

Acknowledgements n Dr. Lukishova n Anand Jha n 243 W Staff: Prof Howell, Steve Bloch

Questions?

Bell’s Inequalities & HVT Presently n Loopholes in setup: n Detector n Static polarizers n QUEST = QUantum Entanglement in Space Experimen. Ts (ESA) A. Zeilinger. Oct. 20, 2008. “Photonic Entanglement and Quantum Information” Plenary Talk at OSA Fi. O/DLS XXIV 2008, Rochester, NY.
- Slides: 24