QCD haute nergie et geometric scaling Cyrille Marquet

QCD à haute énergie et « geometric scaling » Cyrille Marquet Service de Physique Théorique CEA/Saclay

Diffusion profondément inélastique (DIS) pour sonder la structure du proton • variables cinématiques: k’ k résolution transverse 1/Q virtualité du photon Q 2 = - (k-k’)2 > 0 énergie dans le centre de masse *p W 2 = (k-k’+p)2 on utilise la variable de Bjorken x: et on exprime la section efficace totale *p en fonction de x et Q² DIS(x, Q 2)

Données expérimentales mesures effectuées au collisioneur HERA par les collaborations H 1 et ZEUS sur un grand domaine cinématique cette figure représente la fonction de structure aux valeurs de x intermédiaires: scaling de bjorken F 2(x) violations du scaling: preuve de la présence des gluons

Le « geometric scaling » Stasto, Golec-Biernat et Kwiecinski (2001) Quand on représente la même section efficace en fonction de la variable Q² x on obtient une courbe de scaling: avec Q 0 1 Ge. V et 0. 3 Ce phénomène a été appelé « geometric scaling » il identifie une échelle d’impulsion, intrinsèque au proton, qui augmente quand x décroît: Q 0 x- /2 Peut-on comprendre cela à partir de QCD?

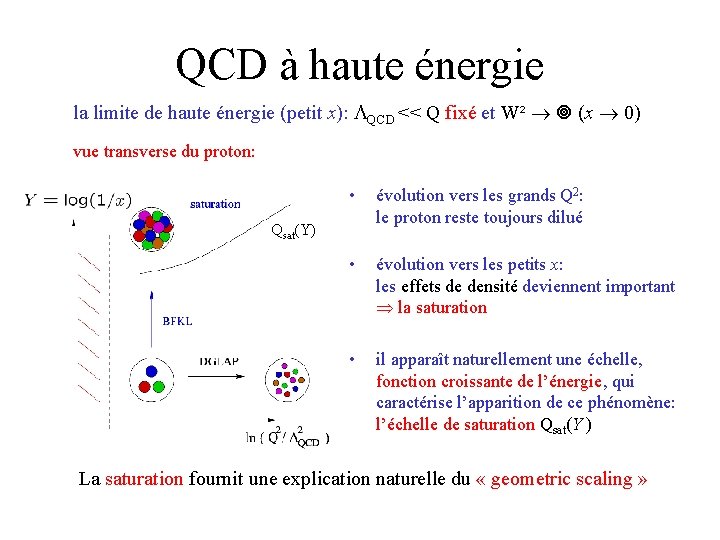
QCD à haute énergie la limite de haute énergie (petit x): QCD << Q fixé et W² (x 0) vue transverse du proton: • évolution vers les grands Q 2: le proton reste toujours dilué • évolution vers les petits x: les effets de densité deviennent important la saturation • il apparaît naturellement une échelle, fonction croissante de l’énergie, qui caractérise l’apparition de ce phénomène: l’échelle de saturation Qsat(Y ) Qsat(Y) La saturation fournit une explication naturelle du « geometric scaling »

La formulation des dipôles L’interaction du photon avec le proton est « remplacée » par l’interaction d’un dipôle: une paire qq singlet de couleur Mueller; Nikolaev et Zakharov (1994) x: position transverse du quark y: position transverse de l’antiquark fonction d’onde k’ k Tqq : amplitude de collision du dipôle avec le proton r = x-y: taille du dipôle

L’équation de Balitsky-Kovchegov Balitsky (1996); Kovchegov (1998) L’équation BK est une équation qui décrit l’évolution avec Y de : la dépendence en Y de est sous-entendue c’est une approximation d’équations plus élaborées qui contient la physique suivante: à petit Y, est petit, et on peut négliger le terme l’équation devient l’équation linéaire BFKL quand Y augmente, est proportionel à augmente exponentiellement avec Y quand approche 1 (le point fixe stable de l’équation), le terme non linéaire devient inportant, et sature à 1

Solutions de l’équation BFKL Etudions d’abord le cas où Considérons la transformée de Fourier: avec Solutions de l’équation BFKL: une superposition d’ondes progressives échelle introduite par la condition initiale en espace de Mellin : noyau BFKL en espace de Mellin avec

Solutions de l’équation BK Comme la condition initiale est assez décroissante à grand Munier et Peschanski (2004) Solutions asymptotiques de l’équation BK: une onde progressive particulière: celle de vitesse minimale Y >Y 0 L implique pour la section efficace mesurée: « geometric scaling »

« geometric scaling » dans les processus exclusifs C. M. , R. Peschanski and G. Soyez, Nucl. Phys. A 756 (2005) 399 C. M. and G. Soyez, Nucl. Phys. A 760 (2005) 208

Au delà du cas On relaxe l’approximation On considére maintenant la transformée de Fourier: L’équation BK pour s’écrit la dépendence en Y de est sous-entendue L’analyse des solutions de l’équation linéaire (BFKL) permet de prédire la forme des solutions asymptotiques pour l’équation complete: : trace de la condition initiale Le résultat est identique au cas précédent, mais avec le changement

Conséquences pour la phénoménologie Conséquence: on prédit le « geometric scaling » dans les processus exclusifs Exemple en DIS : la diffusion Compton en termes de dipôles la section efficace s’écrit avec -q² = t t = (p-p’)² ’ est l’amplitude de collision du dipôle dans un espace mixte r : taille du dipôle L’analyse précédente donne On prédit donc q : transfer d’impulsion