Projekt OP VK CZ 1 071 5 0034














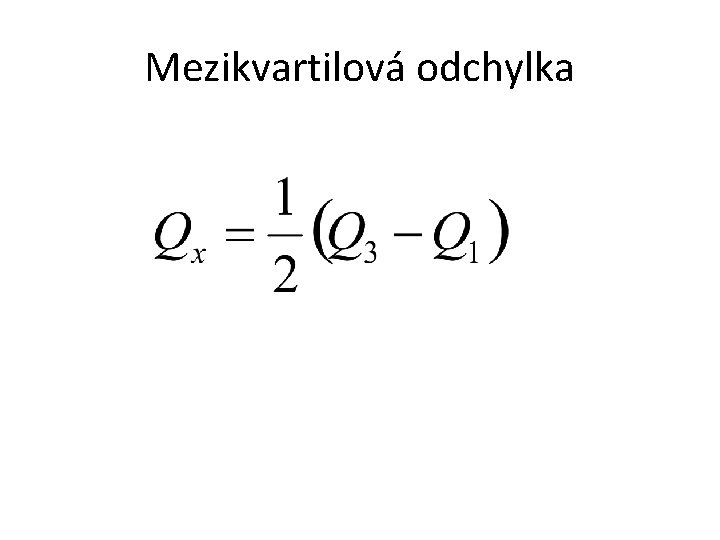



- Slides: 20

Projekt OP VK č. CZ. 1. 07/1. 5. 00/34. 0420 Šablony Mendelova střední škola, Nový Jičín NÁZEV MATERIÁLU: Statistika – charakteristiky variability Autor: Marie Vraná Rok vydání: 2013 Tento projekt je spolufinancován ESF a státním rozpočtem ČR. Byl uskutečněn z prostředků projektu OP VK. Materiály jsou určeny pro bezplatné používání pro potřeby výuky a vzdělávání na všech typech škol a školských zařízení. Jakékoliv další využití podléhá Autorskému zákonu. Materiál je publikován pod licencí Creative Commons – Uveďte autora - Neužívejte komerčně - Nezasahujte do díla 3. 0 Česko.

Odchylky od středních hodnot slon 5 000 kg myš 0, 030 kg průměrná hodnota je 2 500 kg

Odchylky od středních hodnot Popis statistického souboru pomocí středních hodnot někdy nestačí Soubor č. 1: 5, 4, 7, 8, 5, 8, 4, 6, 7, 7, 5, 4, 8 Soubor č. 2: 3, 4, 5, 7, 4, 10, 8, 7, 4, 5, 2, 8, 9, 8 Vypočítejte aritmetické průměry. Čím se oba soubory od sebe liší?

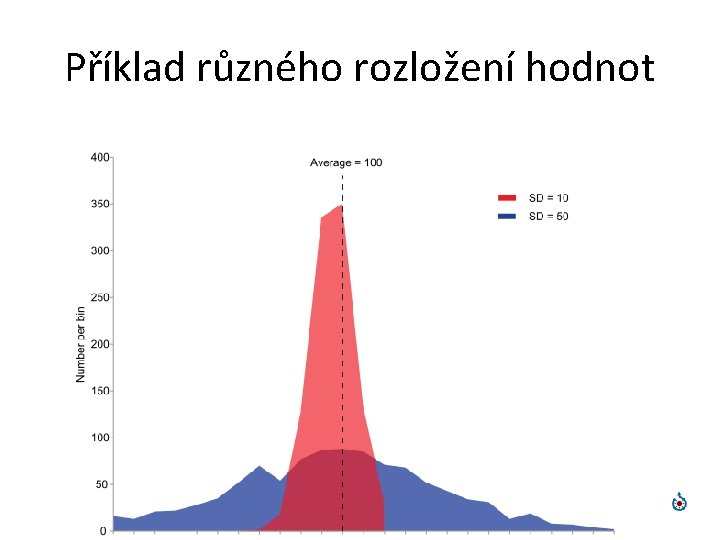
Odchylky od středních hodnot Vzdálenosti dat prvního souboru od aritmetického průměru je menší než u druhého souboru. Velikost kolísání hodnot kolem střední hodnoty je vyjádřena charakteristikami variability (proměnlivosti) znaku.

Příklad různého rozložení hodnot

Charakteristiky variability • • • Rozptyl Směrodatná odchylka Variační koeficient Mezikvartilová odchylka …… a mnoho dalších

Absolutní odchylky Součet všech odchylek od aritmetického průměru je vždy roven nule nelze přímo využít

Rozptyl • Průměr druhých mocnin odchylek od aritmetického průměru • Označujeme jej nebo

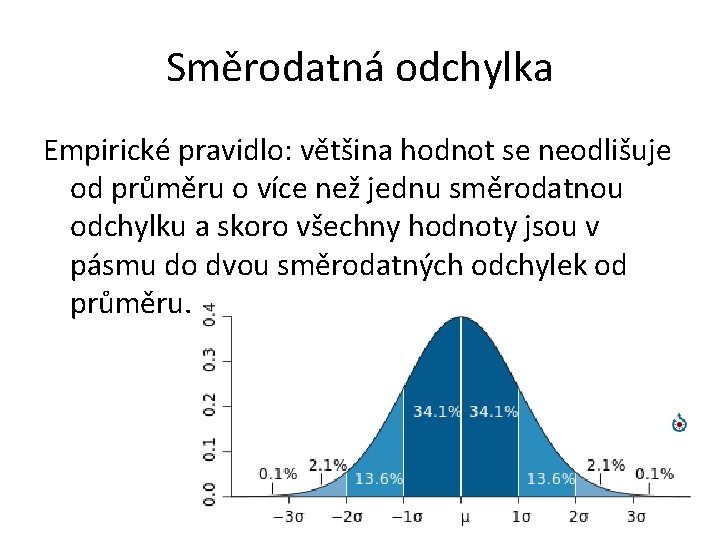
Směrodatná odchylka • Druhá odmocnina z rozptylu. • Označujeme ji nebo Výhoda: – stejné jednotky jako hodnota znaku

Rozptyl a směrodatná odchylka • Vypočítejte rozptyl a směrodatnou odchylku souborů č. 1 a 2 Soubor č. 1: 5, 4, 7, 8, 5, 8, 4, 6, 7, 7, 5, 4, 8 Soubor č. 2: 3, 4, 5, 7, 4, 10, 8, 7, 4, 5, 2, 8, 9, 8

xi xi - (xi - )2 4 -2 4 5 -1 1 6 0 0 7 1 1 8 2 4 0 32

xi xi - (xi - )2 2 -4 16 3 -3 9 4 -2 4 5 -1 1 7 1 1 8 2 4 9 3 9 10 4 16 0 78

Směrodatná odchylka Empirické pravidlo: většina hodnot se neodlišuje od průměru o více než jednu směrodatnou odchylku a skoro všechny hodnoty jsou v pásmu do dvou směrodatných odchylek od průměru.

Variační koeficient • Charakterizuje variabilitu znaku bezrozměrným číslem • Podíl směrodatné odchylky a aritmetického průměru • Vyjadřuje se obvykle v procentech • Variační koeficient má smysl jen pokud znak nabývá jen nezáporných hodnot

Úloha Deset opakovaných měření nějaké fyzikální konstanty dalo tyto výsledky x 1 až x 10 : 2, 11; 2, 09; 2, 02; 2, 11; 2, 03; 2, 10; 2, 05 Vypočtěte průměr, směrodatnou odchylku a variační koeficient. http: //www. kalkulacka. info/statistickevypocty

Jiné charakteristiky polohy Pokud místo aritmetického průměru použijeme medián, musíme použít mezikvartilovou odchylku: Medián = „prostřední“ hodnota První kvartil Q 1 = „čtvrtinová“ hodnota (medián první poloviny hodnot) Třetí kvartil Q 3 = „tříčtvrtinová“ hodnota (medián druhé poloviny hodnot)
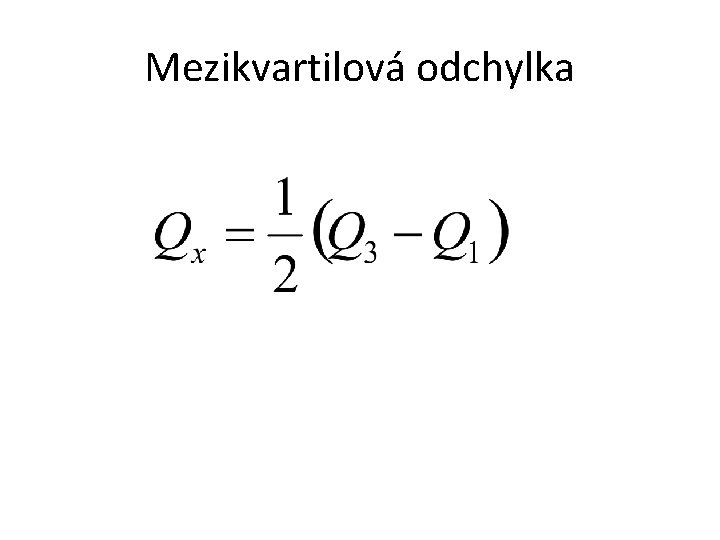
Mezikvartilová odchylka

Mezikvartilová odchylka Vypočítejte směrodatnou a mezikvartilovou odchylku v úloze z předcházející hodiny: Roční příjem 200 240 260 280 350 950 četnost 1 7 6 4 1 1 Q 1 = 240 000 Kč Q 2 = 280 000 Kč Qx = 20 000 Kč sx = ?

Úlohy Pracovní list charakteristiky polohy a variability

Zdroje CALDA, Emil, DUPAČ, Václav. Matematika pro gymnázia. Kombinatorika, pravděpodobnost, statistika. Praha: Prometheus, 2006. Wikimedia Commons Creative Commons. [cit. 8. 5. 2013]. Dostupné z: http: //cs. wikipedia. org/wiki/Soubor: Comparison_standard_deviations. svg JRBrown http: //cs. wikipedia. org/wiki/Soubor: Standard_deviation_diagram. svg Vlastní dílo, based (in concept) on figure by Jeremy Kemp, on 2005 -02 -09
 Příklady na mocniny s racionálním exponentem
Příklady na mocniny s racionálním exponentem Pb 071
Pb 071 071-com-4407
071-com-4407 Terrain features draw
Terrain features draw N 3^071
N 3^071 Reacting to indirect fire
Reacting to indirect fire ?3305501049 0000 28|.|091 27|.|071 98|.|553 102|.|311 13`
?3305501049 0000 28|.|091 27|.|071 98|.|553 102|.|311 13` 071 atm code
071 atm code 071-com-4407
071-com-4407 Discipline of light refraction
Discipline of light refraction Perform surveillance without the aid of electronic device
Perform surveillance without the aid of electronic device 071-com-0029
071-com-0029 Pb 071
Pb 071 Vlera nominale
Vlera nominale Bioenergjia
Bioenergjia Jeta e shekspirit
Jeta e shekspirit Tipski projekt
Tipski projekt Projekt organisationsstruktur
Projekt organisationsstruktur Dhuna projekt
Dhuna projekt Projekt esettanulmány minta ppt
Projekt esettanulmány minta ppt Projekt erőforrás tervezés
Projekt erőforrás tervezés







































