CS 105 Digital Logic Design Sem 1 1436

CS 105 Digital Logic Design Sem 1 -1436 -1437 Chapter 1 Lecturer Fawziah Alqahtani

2 Contents Communication Course Information. Text book. Grades. Exams dates. Topics to be covered. Digital Systems and Computer Systems Information Representation Number Systems [binary, octal and hexadecimal]

Communication Office hours (7 hours per Week): Sunday (9 -9: 50) & (2: 30 – 4: 00). Tuesday (9 -9: 50) & (2: 30 – 4: 00). Thursday (9 -9: 50). E-mail: iamfawziah@yahoo. com E-Learning: Blackboard

Textbook “DIGITAL DESIGN”, by Mano M. Morris, 4 th edition, Prentice- Hall.

Midterm Dates & Grades Check the handout!

6 42 - ﺍﻟﺜﺎﻧﻲ ﺭﺑﻴﻊ 22 - Conduct in Class Don’t distract the students. I don’t insist that you pay attention, but you must allow others to participate. This eans: o o o Do not distract others with conversation. Do not distract others with your phone. Do not distract others by using your laptop in front of the class. If you snore, I will wake you up. Do not attend the class late; you have only 10 minutes to attend it. Otherwise, you will be marked absent on hat day. There are no makeup quizzes (if you miss a quiz, you will get zero for that quiz). Computer Science Department

7 42 - ﺍﻟﺜﺎﻧﻲ ﺭﺑﻴﻊ 22 - Rules of e-mail messages: Write your message in paschal Arabic (NOT in slang Arabic). In the email Subject, you have to write: Course#- Section# - full Name – brief description for the email , for example: CS 105 D-1 C 10 – Nora Al. Ahmad – about sheet 1 CS 105 D-11 C 12– Sara Al. Ali – about. . . In general, subject should summarize the message. We will not reply to any email that contains something like: ? ? ? !!!!! , or ﻫﺎﺍﺍﺍﺍﺍﺍﻡ or ﺃﺮﺟﻮ ﺍﻟﺮﺩ , or any impolite words. If you violate any one of the above rules, your email will not be opened. NOTE: Send the email from your @pnu. edu. sa address only. Computer Science Department

8 42 - ﺍﻟﺜﺎﻧﻲ ﺭﺑﻴﻊ 22 - Computer Science Department

Topics to be covered Digital Systems and Binary numbers Boolean Algebra and Logic Gates Gate Level Minimization Combinational Logic Synchronous Sequential Logic

Chapter 1 Outline 1. 1 Digital Systems 1. 2 Binary Numbers 1. 3 Number-Base Conversions 1. 4 Octal and Hexadecimal Numbers 1. 5 Complements 1. 6 Signed Binary Numbers 1. 7 Binary Codes

1. 1 Digital Systems (1 -2) Digital system is a system that uses discrete values such as numbers and letters. The signal in most digital systems use two values : 0 and 1 which called a bit. Discrete elements of information are represented with a group of bits called binary codes. Thus, Digital system is a system that manipulates discrete elements of information represented internally in binary form.

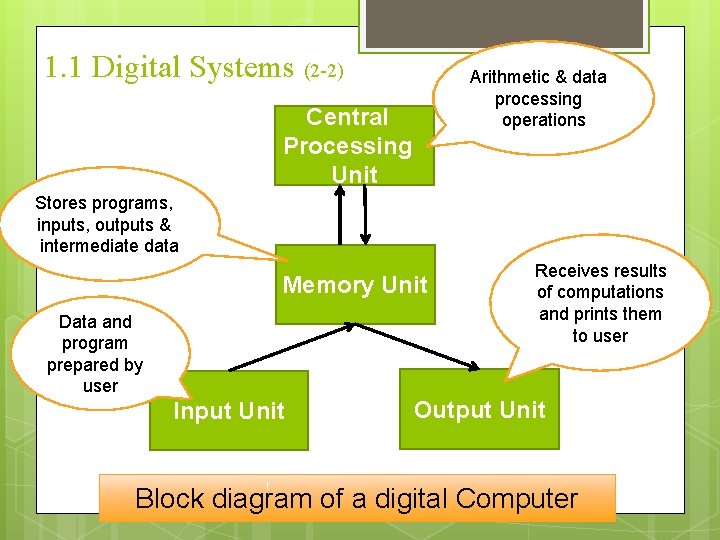
1. 1 Digital Systems (2 -2) Central Processing Unit Arithmetic & data processing operations Stores programs, inputs, outputs & intermediate data Memory Unit Data and program prepared by user Input Unit Receives results of computations and prints them to user Output Unit Block diagram of a digital Computer

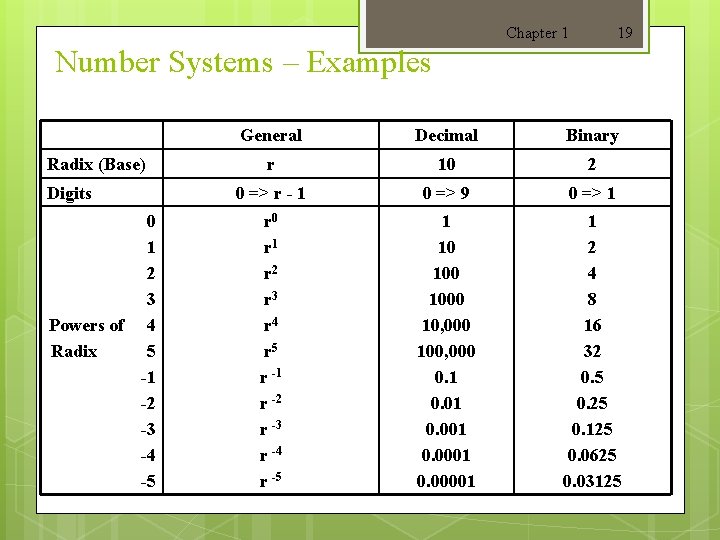
1. 2 Binary Numbers Number Systems – Representation Chapter 1 13 Positive radix, positional number systems A number with radix r is represented by a string of digits: An - 1 An - 2 … A 1 A 0. A- 1 A- 2 … A- m + 1 A- m in which 0 £ Ai < r and. is the radix point. The string of digits represents the power series: (å i=n-1 (Number)r = i=0 Ai r ) ( å j=-1 i j=-m Aj r) j (Integer Portion) + (Fraction Portion)

1. 2 Binary Numbers (Cont. ) In general, a number expressed in a base-r system has coefficients multiplied by powers of r: An-1. rn-1 + An-2. rn-2 +. . . . + A 2. r 2 + A 1. r + A 0 + A-1. r-1 + A-2. r-2 +. . + a-m. r-m r is called base or radix. Aj ranges in thr value from 0 to r-1

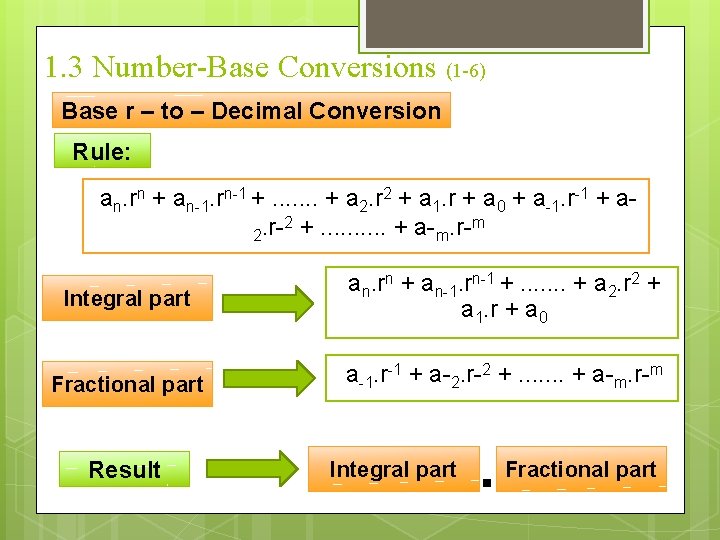
1. 3 Number-Base Conversions (1 -6) Base r – to – Decimal Conversion Rule: an. rn + an-1. rn-1 +. . . . + a 2. r 2 + a 1. r + a 0 + a-1. r-1 + a 2 +. . + a-. r-m. r 2 m Integral part an. rn + an-1. rn-1 +. . . . + a 2. r 2 + a 1. r + a 0 Fractional part a-1. r-1 + a-2. r-2 +. . . . + a-m. r-m Result Integral part Fractional part

1. 3 Number-Base Conversions (2 -6) Base r – to – Decimal Conversion Example: Find the decimal equivalent ofthe binary number (1001. 0101)2. Integral part Fractional part Result 1001 = 1 x 23 + 0 x 22 + 0 x 21 + 1 x 20 = 8+0+0+1=9 . 0101 = 0 x 2 -1 + 1 x 2 -2 + 0 x 2 -3 + 1 x 2 -4 = 0+. 25+0+0. 0625=0. 3125 (9. 3125)10

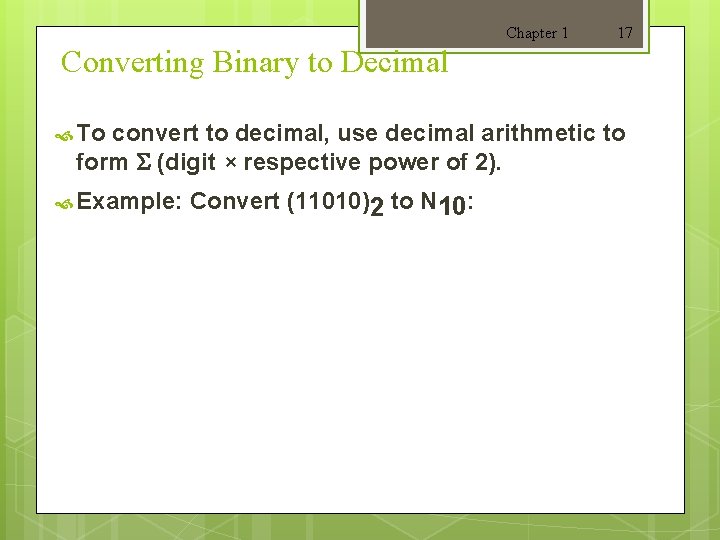
Chapter 1 17 Converting Binary to Decimal To convert to decimal, use decimal arithmetic to form S (digit × respective power of 2). Example: Convert (11010)2 to N 10:

1. 3 Number-Base Conversions (3 -6) Base r – to – Decimal Conversion Example: (1010. 011)2= 23 + 21 + 2 -2 + 2 -3 =(10. 375)10 (127. 4)8 = 1 x 82 + 2 x 81 + 7 x 80 + 4 x 8 -1 = (87. 5)10 (1101)2 = 1 x 23 + 1 x 22 + 0 x 21 + 1 x 20 = (13)10

Chapter 1 19 Number Systems – Examples Radix (Base) Digits 0 1 2 3 Powers of 4 Radix 5 -1 -2 -3 -4 -5 General Decimal Binary r 10 2 0 => r - 1 0 => 9 0 => 1 r 0 r 1 r 2 r 3 r 4 r 5 r -1 r -2 r -3 r -4 r -5 1 10 1000 10, 000 100, 000 0. 1 0. 001 0. 00001 1 2 4 8 16 32 0. 5 0. 25 0. 125 0. 0625 0. 03125

1. 2 Binary Numbers (Cont. ) Numbering System Base Decimal 10 Binary 2 Octal 8 Hexadecimal 16 Symbols 0, 1, 3, 4, 5, 6, 7, 8, 9 0, 1, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F The six letters (in addition to the 10 integers) in hexadecimal represent ? ?

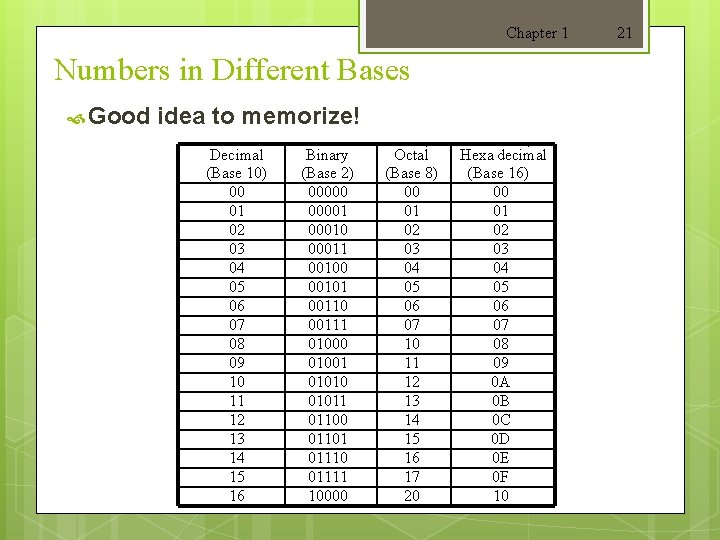
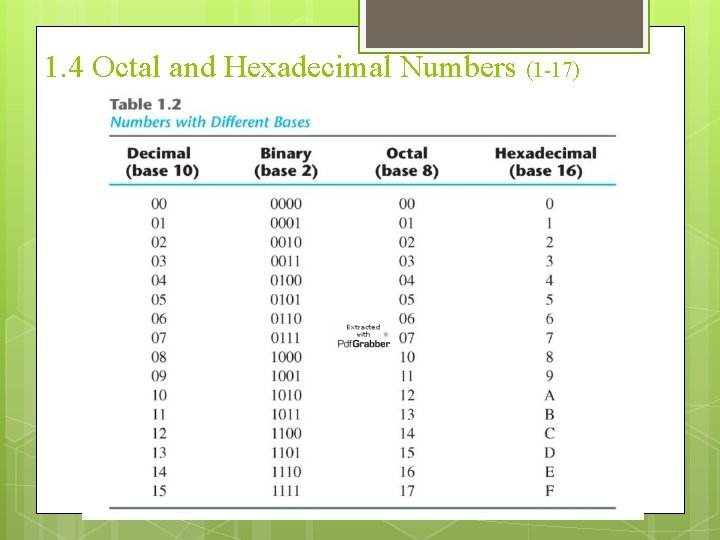
Chapter 1 Numbers in Different Bases Good idea to memorize! Decimal (Base 10) 00 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 Binary (Base 2) 000001 00010 00011 00100 00101 00110 00111 01000 01001 01010 01011 01100 01101 01110 01111 10000 Octal (Base 8) 00 01 02 03 04 05 06 07 10 11 12 13 14 15 16 17 20 Hexa decimal (Base 16) 00 01 02 03 04 05 06 07 08 09 0 A 0 B 0 C 0 D 0 E 0 F 10 21

Chapter 1 22 Special Powers of 2 210 (1024) is Kilo, denoted "K" 220 (1, 048, 576) is Mega, denoted "M" 230 (1, 073, 741, 824)is Giga, denoted "G"

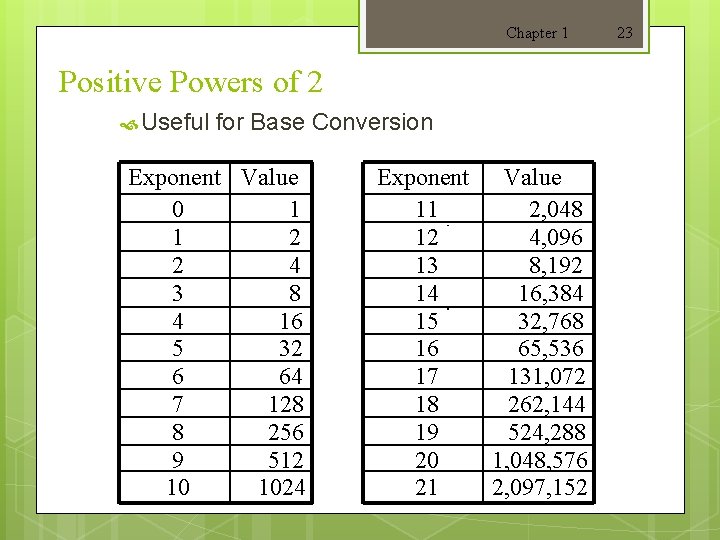
Chapter 1 Positive Powers of 2 Useful for Base Conversion Exponent Value 0 1 1 2 2 4 3 8 4 16 5 32 6 64 7 128 8 256 9 512 10 1024 Exponent Value 11 2, 048 12 4, 096 13 8, 192 14 16, 384 15 32, 768 16 65, 536 17 131, 072 18 262, 144 19 524, 288 20 1, 048, 576 21 2, 097, 152 23

1. 2 Binary Numbers (4 -6) Arithmetic Operations Follow the same rules of as for decimal numbers Addition Carries 00000 Carries 101100 Augend 10110 Addend + 10001 Addend + 10111 Sum 11101 Sum 101101

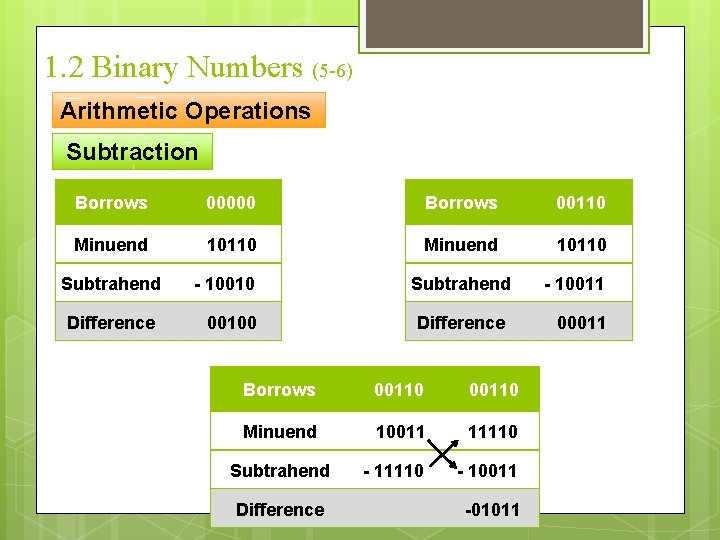
1. 2 Binary Numbers (5 -6) Arithmetic Operations Subtraction Borrows 00000 Borrows 00110 Minuend 10110 Subtrahend - 10011 Difference 00100 Difference 00011 Borrows 00110 Minuend 10011 11110 Subtrahend - 11110 - 10011 Difference -01011

1. 2 Binary Numbers (6 -6) Arithmetic Operations Multiplication Multiplicand 1011 Multiplier X 1011 0000 1011 Product 110111

Chapter 1 Remember to review 27

Chapter 1 28 1. 3 Number-Base Conversions Converting Decimal to Binary Method 1 Subtract the largest power of 2 (see slide 14) that gives a positive remainder and record the power. Repeat, subtracting from the prior remainder and recording the power, until the remainder is zero. Place 1’s in the positions in the binary result corresponding to the powers recorded; in all other positions place 0’s. Example: Convert 62510 to N 2

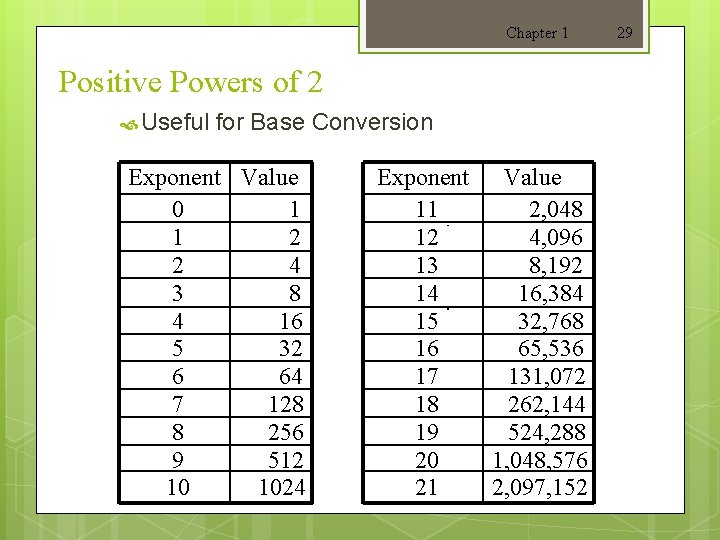
Chapter 1 Positive Powers of 2 Useful for Base Conversion Exponent Value 0 1 1 2 2 4 3 8 4 16 5 32 6 64 7 128 8 256 9 512 10 1024 Exponent Value 11 2, 048 12 4, 096 13 8, 192 14 16, 384 15 32, 768 16 65, 536 17 131, 072 18 262, 144 19 524, 288 20 1, 048, 576 21 2, 097, 152 29

1. 3 Number-Base Conversions (4 -6) Decimal – to – Base r Conversion Rule: Convert each part differently. Integral part Fractional part Result Divide number & its quotients by r. Accumulate reminders. Multiply number & its quotients by r. Accumulate integers. Integral part Fractional part

1. 3 Number-Base Conversions (5 -6) Decimal – to – Base r Conversion Example: Find the binary equivalent of the decimal number (41)10. Integer Reminder 41 Divide by 2 20 1 10 0 5 0 2 1 1 0 0 1 Result (101001)2

1. 3 Number-Base Conversions (6 -6) Decimal – to – Base r Conversion Example: Find the binary equivalent of the decimal number (0. 6875)10. Multiply by 2 Integer Fraction 0. 6875 1 0. 3750 0 0. 7500 Result 0. 7500 1 0. 5000 (0. 1011)2 0. 5000 1 0. 0000

1. 4 Octal and Hexadecimal Numbers (1 -17)

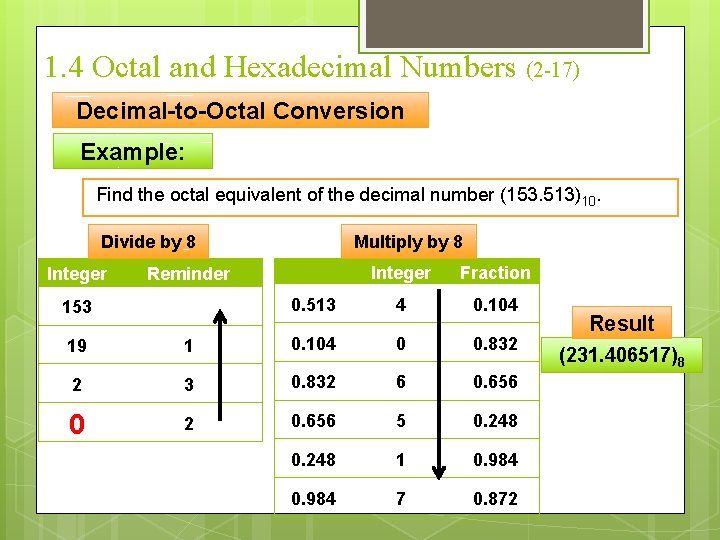
1. 4 Octal and Hexadecimal Numbers (2 -17) Decimal-to-Octal Conversion Example: Find the octal equivalent of the decimal number (153. 513)10. Divide by 8 Integer Multiply by 8 Integer Fraction 0. 513 4 0. 104 Reminder 153 19 1 0. 104 0 0. 832 2 3 0. 832 6 0. 656 0 2 0. 656 5 0. 248 1 0. 984 7 0. 872 Result (231. 406517)8

1. 4 Octal and Hexadecimal Numbers (3 -17) Octal-to-Decimal Conversion Example: Find the decimal equivalent ofthe octal number (137. 21)8. Integral part 137= 1 x 82 + 3 x 81 + 7 x 80 = 64+24+7=95 Fractional part . 21 = 2 x 8 -1 + 1 x 8 -2 =0. 265 Result (95. 265)10

1. 4 Octal and Hexadecimal Numbers (4 -17) Decimal-to-Hexadecimal Conversion Example: Find the hexadecimal equivalent of the decimal number (82. 25)10. Divide by 16 Integer Multiply by 16 Reminder 0. 25 82 5 2 0 5 Result (52. 4)16 Integer Fraction 4 . 0000

1. 4 Octal and Hexadecimal Numbers (5 -17) Hexadecimal-to-Decimal Conversion Example: Find the decimal equivalent ofthe hexadecimal number (1 E 0. 2 A)16. Integral part 1 E 0= 1 x 162 + 14 x 161 + 0 x 160 = 256+224+0=480 Fractional part . 2 A = 2 x 16 -1 + 10 x 16 -2 =0. 164 Result (480. 164)10

1. 4 Octal and Hexadecimal Numbers (6 -17) Binary–Octal and Octal–Binary Conversions Binary – Octal Rule: Divide integral part into three bits starting from right integral bit. Divide fractional part into three bits starting from left fractional bit. Adding zero‘s if necessary.

1. 4 Octal and Hexadecimal Numbers (7 -17) Binary–Octal and Octal–Binary Conversions Example: Find the octal equivalent ofthe binary number (1110100111)2. 001 110 100 . 010 011 100 (1 6 4 . 2 3 4)8

1. 4 Octal and Hexadecimal Numbers (8 -17) Binary–Octal and Octal–Binary Conversions Octal – Binary Rule: BOTH integral and fractional parts: Convert each digit seperately into binary of three bits

1. 4 Octal and Hexadecimal Numbers (9 -17) Binary–Octal and Octal–Binary Conversions Example: Find the binary equivalent ofthe octal number (374. 26)8. 3 7 4 . 2 6 011 100 . 010 110 (11 100 . 010 11)2

1. 4 Octal and Hexadecimal Numbers (10 -17) Binary–Hex and Hex–Binary Conversions Binary – Hex Rule: Divide integral part into four bits starting from right integral bit. Divide fractional part into four bits starting from left fractional bit. Adding zero‘s if necessary.

1. 4 Octal and Hexadecimal Numbers (11 -17) Binary–Hex and Hex–Binary Conversions Example: Find the hexdecimal equivalent ofthe binary number (1011001110. 01101)2. 0010 1100 1110 . 0110 1000 (2 C E . 6 E 8)16

1. 4 Octal and Hexadecimal Numbers (12 -17) Binary–Hex and Hex–Binary Conversions Hex – Binary Rule: BOTH integral and fractional parts: Convert each digit seperately into binary of four bits

1. 4 Octal and Hexadecimal Numbers (13 -17) Binary–Hex and Hex–Binary Conversions Example: Find the binary equivalent ofthe hexadecimal number (17 E. F 6)16. 1 7 E . F 6 0001 0111 1110 . 1111 0110 (1 0111 1110 . 1111 011)2

1. 4 Octal and Hexadecimal Numbers (14 -17) Hex–Octal and Octal–Hex Conversions Hex – Octal Rule: Convert Hex number into binary. Convert the result binary number into octal. OR Convert Hex number into decimal. Convert the result decimal number into octal.

1. 4 Octal and Hexadecimal Numbers (15 -17) Hex–Octal and Octal–Hex Conversions Example: Find the Hex equivalent ofthe octal number (762. 013)8. 7 6 2 . 0 1 3 Binary (0001 1111 0010. 0000 0101 1 000) 000 2 Hex (1 F 2 . 0 5 8)16

1. 4 Octal and Hexadecimal Numbers (16 -17) Hex–Octal and Octal–Hex Conversions Octal – Hex Rule: Convert Octal number into binary. Convert the result binary number into Hex. OR Convert Octal number into decimal. Convert the result decimal number into Hex.

1. 4 Octal and Hexadecimal Numbers (17 -17) Hex–Octal and Octal–Hex Conversions Example: Find the octal equivalent ofthe Hex number (2 F. C 4)16. 2 F . C 4 Binary (000 101 111. 110 001 000) 000 2 Octal (0 5 7 . 6 1 0)8 (5 7 . 6 1)8

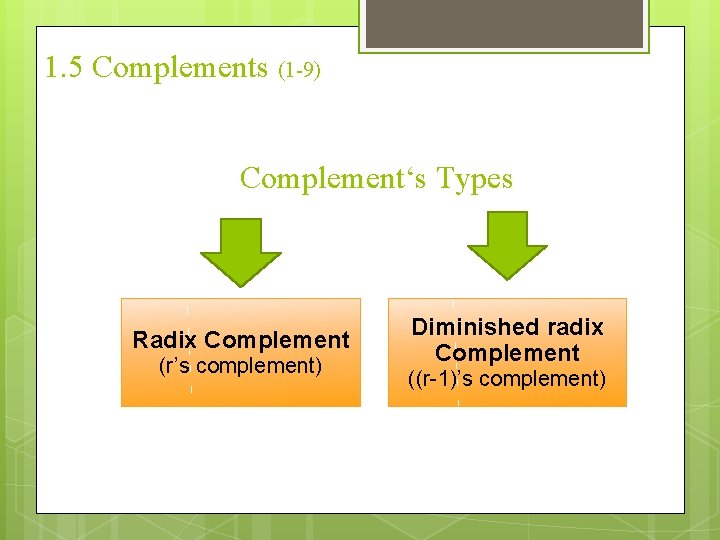
1. 5 Complements (1 -9) Complement‘s Types Radix Complement (r’s complement) Diminished radix Complement ((r-1)’s complement)

1. 5 Complements (1 -9) Diminished Radix Complement ((r-1)‘s complement) Rule o Given a number N in base r having n digits, the (r- 1)’s complement of N is defined as (rn- 1) -N. Examples o o 9’s complement of 546700 is 999999 – 546700= 453299 1’s complement of 1011000 is 0100111. Note o The (r-1)’s complement of octal or hexadecimal numbers is obtained by subtracting each digit from 7 or F (decimal 15), respectively.

1. 5 Complements (2 -9) Radix Complement Rule o Given a number N in base r having n digit, the r’s complement of N is defined as (rn -N) for N ≠ 0 and as 0 for N =0. OR o Adding 1 to (r-1)‘s complement. Examples o o o The 10’s complement of 012398 is 987602 The 10’s complement of 246700 is 753300 The 2’s complement of 1011000 is 0101000

1. 5 Complements (2 -9) Note: The complement of the complement restores the number to its original value.

1. 5 Complements (3 -9) Subtraction with Complement The subtraction of two n-digit unsigned numbers M – N in base r can be done as follows: o M + (rn - N), note that (rn - N) is r’s complement of N. o o If (M N), the sum will produce an end carry x, which can be discarded; what is left is the result M- N. If (M < N), the sum does not produce an end carry and is (N - M). Take the r’x complement of the sum and place a negative sign in front.

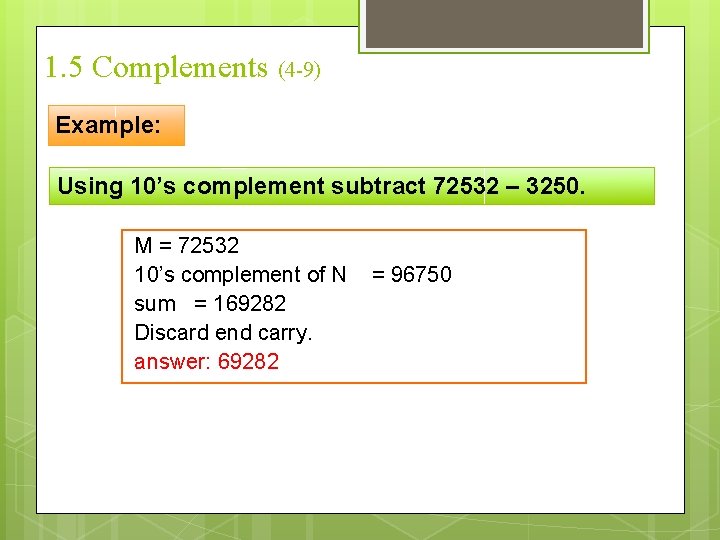
1. 5 Complements (4 -9) Example: Using 10’s complement subtract 72532 – 3250. M = 72532 10’s complement of N = 96750 sum = 169282 Discard end carry. answer: 69282

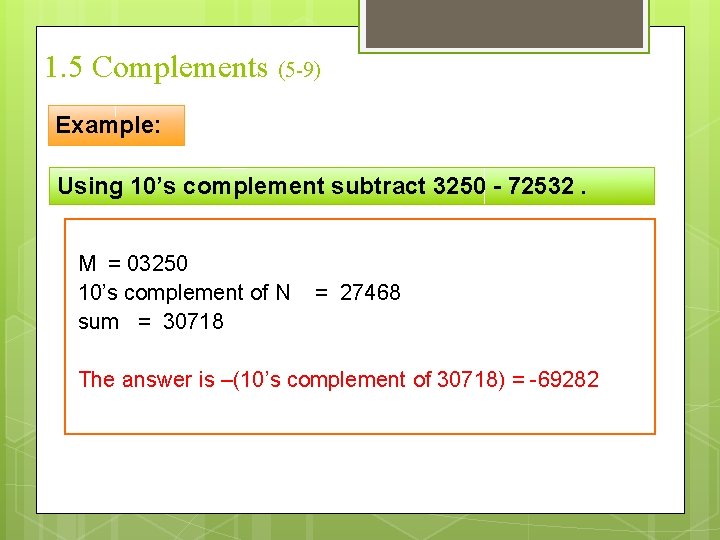
1. 5 Complements (5 -9) Example: Using 10’s complement subtract 3250 - 72532. M = 03250 10’s complement of N = 27468 sum = 30718 The answer is –(10’s complement of 30718) = -69282

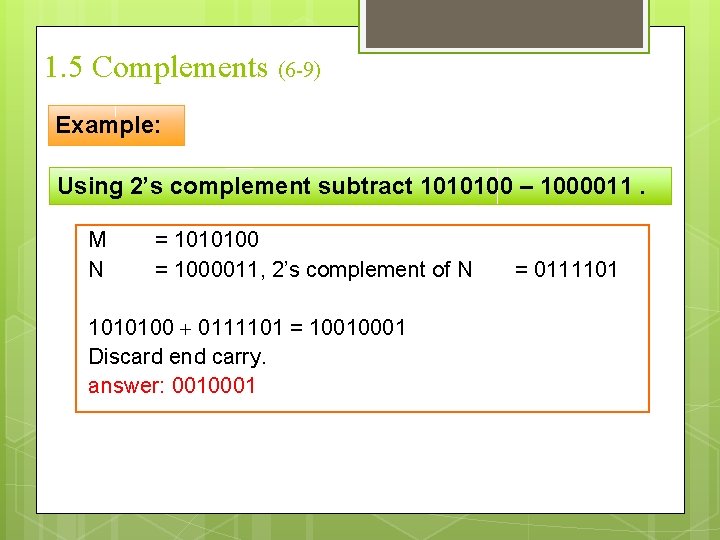
1. 5 Complements (6 -9) Example: Using 2’s complement subtract 1010100 – 1000011. M N = 1010100 = 1000011, 2’s complement of N 1010100 0111101 = 10010001 Discard end carry. answer: 0010001 = 0111101

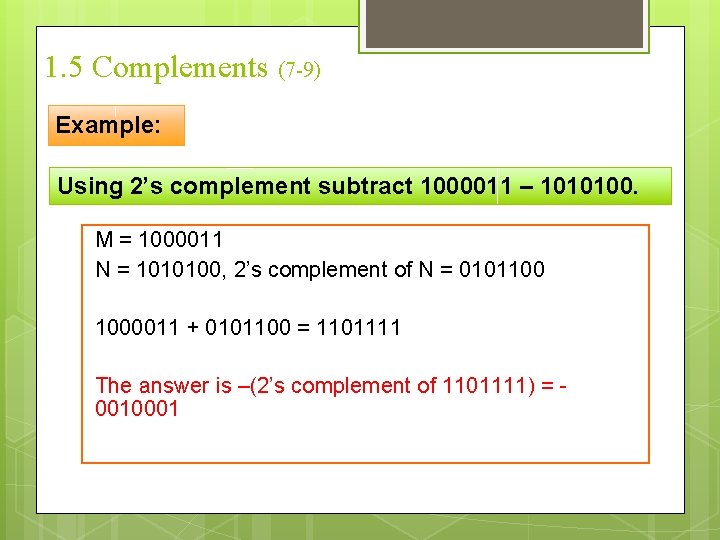
1. 5 Complements (7 -9) Example: Using 2’s complement subtract 1000011 – 1010100. M = 1000011 N = 1010100, 2’s complement of N = 0101100 1000011 + 0101100 = 1101111 The answer is –(2’s complement of 1101111) = 0010001

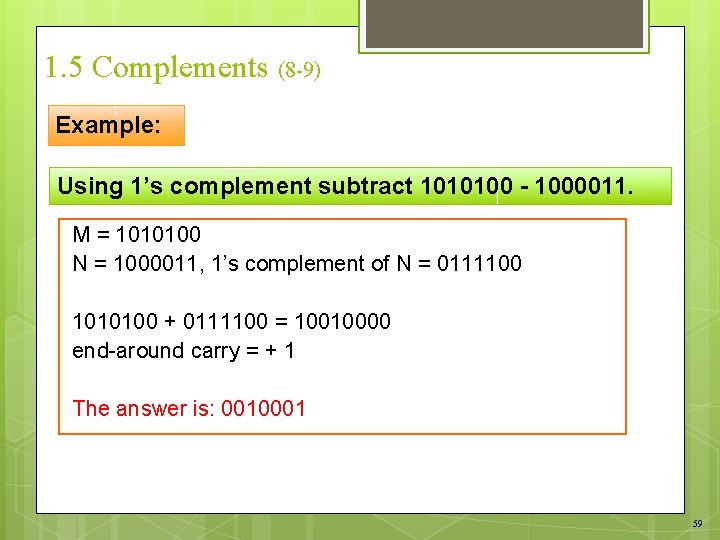
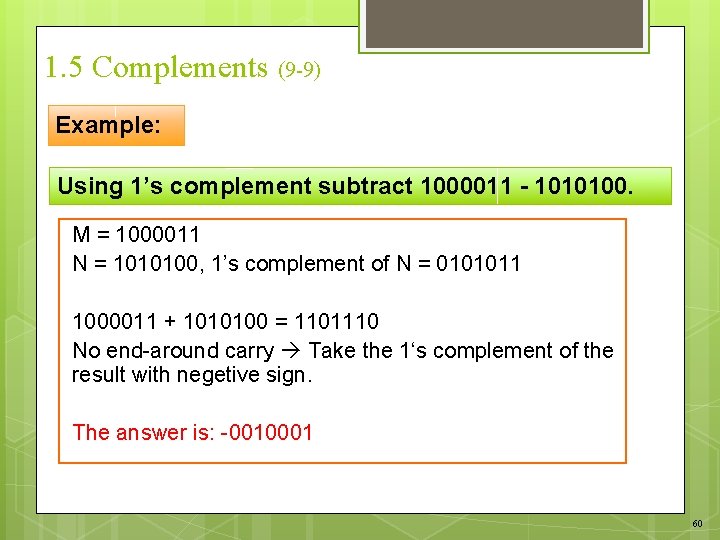
1. 5 Complements (8 -9) Example: Using 1’s complement subtract 1010100 - 1000011. M = 1010100 N = 1000011, 1’s complement of N = 0111100 1010100 + 0111100 = 10010000 end-around carry = + 1 The answer is: 0010001 59

1. 5 Complements (9 -9) Example: Using 1’s complement subtract 1000011 - 1010100. M = 1000011 N = 1010100, 1’s complement of N = 0101011 1000011 + 1010100 = 1101110 No end-around carry Take the 1‘s complement of the result with negetive sign. The answer is: -0010001 60

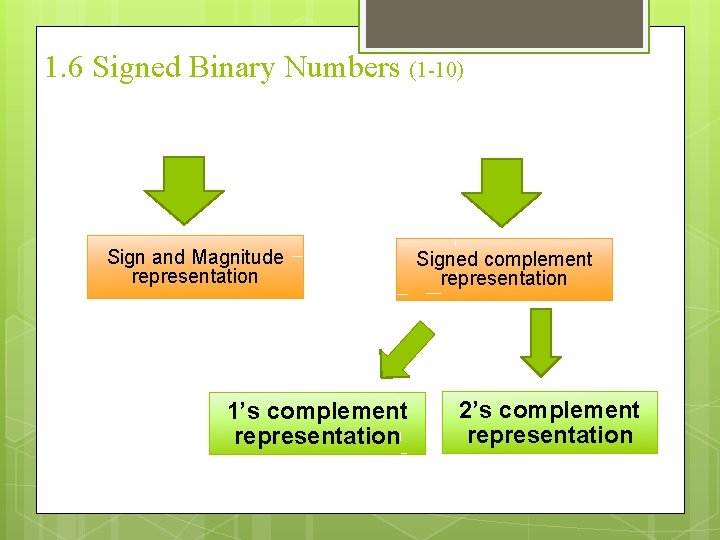
1. 6 Signed Binary Numbers (1 -10) Sign and Magnitude representation 1’s complement representation Signed complement representation 2’s complement representation

1. 6 Signed Binary Numbers (2 -10) Notes: o o o The previous representation (unsigned numbers) are the same for positive numbers and different for negative numbers. For a unsigned binary number the most significant bit is part of the number. For a signed binary number the most significant bit is used for representing the sign of the number and the rest of the bits represent the number. We use 0 for positive numbers and 1 for negative numbers.

1. 6 Signed Binary Numbers (3 -10) Example: Represent +76 (76)10 = (1001100)2 Unsigned number (+76)10 = (01001100)2 Sign & Magnitude (+76)10 = (01001100)2 1’s Complement (+76)10 = (01001100)2 2’s Complement

1. 6 Signed Binary Numbers (4 -10) Negative numbers: 1‘Complement obtained by flipping all bits of the positive binary number 2‘Complement obtained by adding 1 to the 1’s Complement. OR: by flipping bits of the positive binary number after the first one from the right

1. 6 Signed Binary Numbers (5 -10) Negative numbers: Sign & Magnitude obtained by changing the left most bit of the positive binary number to 1. Example: Represent -76 (-76)10 = (1100)2 Sign & Magnitude (-76)10 = (10110011)2 1’s Complement (-76)10 = (10110100)2 2’s Complement

1. 6 Signed Binary Numbers (6 -10) Arithmetic Addition: With Comprison The addition of two numbers in the signed & magnitude system follows the rules of ordinary arithmetic: If the signed are the same, we add the two magnitudes and give the sum the common sign. If the signed are different, we subtract the smaller magnitude from the larger and give the difference the sign of the larger magnitude. EX. (+25) + (-38) = -(38 - 25) = -13

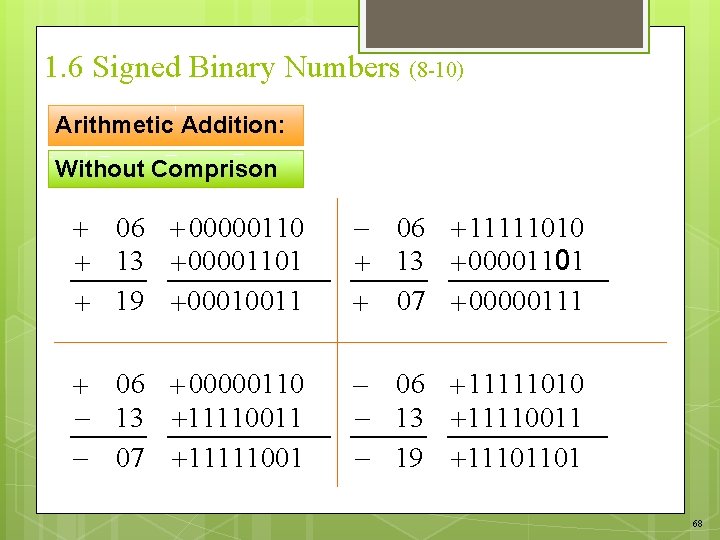
1. 6 Signed Binary Numbers (7 -10) Arithmetic Addition: Without Comprison The addition of two numbers in the signed 2’s complement form is obtained from the addition of the two numbers, including their signed bits. A carry out of the signed bit position is discarded (note that the 4 th case of the example). If the result is negetive (left most bit is one), then the must be complemented to extract its value.

1. 6 Signed Binary Numbers (8 -10) Arithmetic Addition: Without Comprison 06 00000110 13 00001101 19 00010011 06 11111010 13 00001101 07 00000111 06 00000110 13 11110011 07 11111001 06 11111010 13 11110011 19 11101101 68

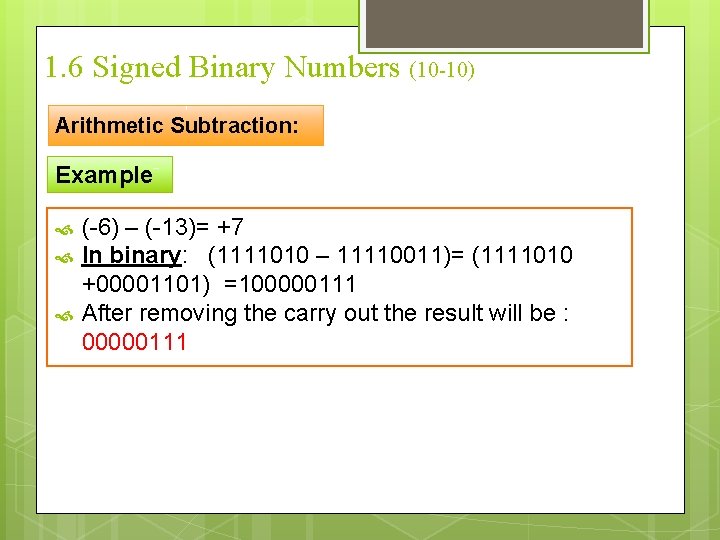
1. 6 Signed Binary Numbers (9 -10) Arithmetic Subtraction: Rule Change the artithmetic operation into addition. Change the sign of the subtrahend (positive to negative or negative to positive). (+/-) A – (+B)= (+/-) A + (-B) (+/-) A – (-B)= (+/-) A + (+B)

1. 6 Signed Binary Numbers (10 -10) Arithmetic Subtraction: Example (-6) – (-13)= +7 In binary: (1111010 – 11110011)= (1111010 +00001101) =100000111 After removing the carry out the result will be : 00000111

1. 7 Binary Codes (1 -24) Any discrete element of information that is distinct among a group of quantities can be represented with a binary code (i. e. a pattern of 0's and 1's). An n-bit binary code is a group of n bits that assumes up to 2" distinct combinations of 1's and 0'r. Each combination representing one element of the set that is being coded. Example A set of four elements can be coded with two bits, with each element assigned one of the following bit combinations: 00. 01. 10. 11.

1. 7 Binary Codes (2 -24) The bit combination of an n-bit code is determined from the count in binary from 0 to 2" - 1. Each element must be assigned a unique binary bit combination and no two elements can have the same value; otherwise. the code assignment will be ambiguous. Minimum number of bits required to code 2" distinct quantities is n. NO Maximum number of bits that may be used for a binary code.

1. 7 Binary Codes (3 -24) BCD Stands for binary-coded decimal. Represents the 10 decimal digits. Each digit is represented in 4 bits. Makes 16 possible combinations. 6 are unassigned. A number with k decimal digits will require 4 k bits in BCD. Weight (8, 4, 2, 1. )

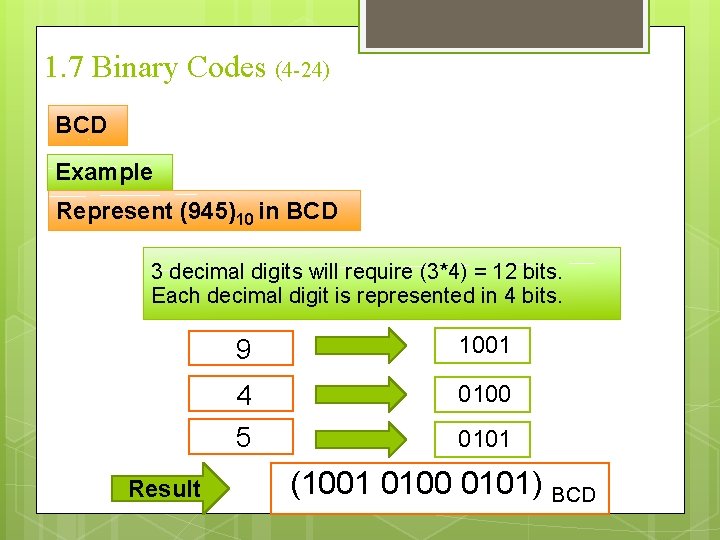
1. 7 Binary Codes (4 -24) BCD Example Represent (945)10 in BCD 3 decimal digits will require (3*4) = 12 bits. Each decimal digit is represented in 4 bits. Result 9 1001 4 0100 5 0101 (1001 0100 0101) BCD

1. 7 Binary Codes (5 -24) BCD Addition Notes Same as adding two decimal numbers. Sum cannot be greater than 9, such as: 9+9+1=19 with 1 is being a previous carry. If the result value was greater than (1001)2=(9) or if the result was more than 4 digits. Then it is an invalid BCD digit. Add (0110)2=(6) to convert it to correct digit. A carry will be produced Result more than 4 digit is greater than 9(1001)

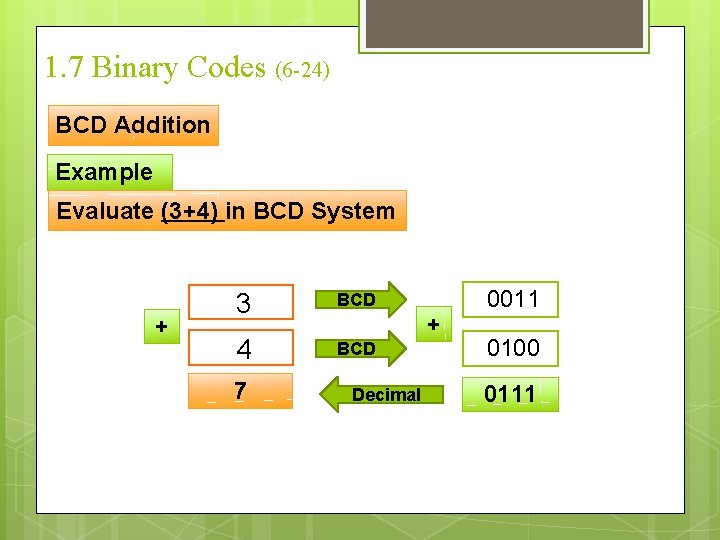
1. 7 Binary Codes (6 -24) BCD Addition Example Evaluate (3+4) in BCD System + 3 BCD 4 BCD 7 + Decimal 0011 0100 0111

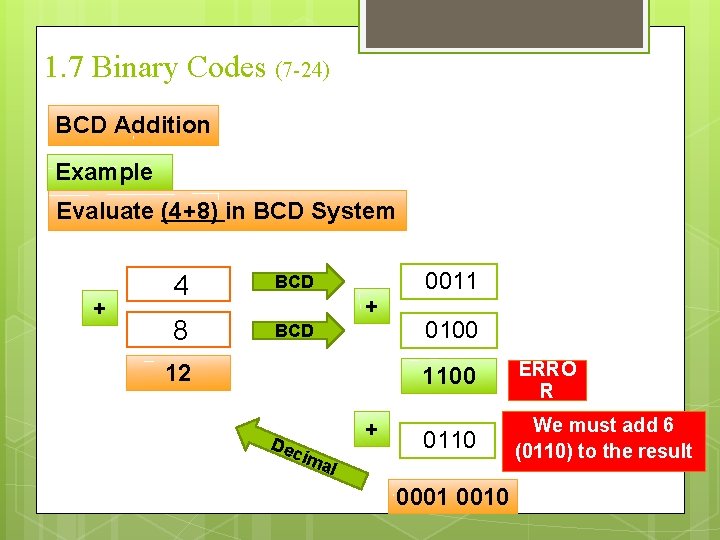
1. 7 Binary Codes (7 -24) BCD Addition Example Evaluate (4+8) in BCD System + 4 BCD 8 BCD + 12 Dec + ima 0011 0100 1100 ERRO R 0110 We must add 6 (0110) to the result l 0001 0010

1. 7 Binary Codes (8 -24) BCD Addition Example Evaluate (184+576) in BCD System + 184 BCD 576 BCD + 760 Dec + 0001 1000 0101 1 0111 1 10000 0110 1010 0110 1 0000 ima l 0111

1. 7 Binary Codes (9 -24) Decimal Arithmetic Signed numbers Signed decimal numbers in BCD similar to signed numbers in binary. Can be signed-magnitude system or signed-complement system (9‘s or 10‘s complement) Sign represented with four bits in BCD. + -> 0000 (four 0‘s). - -> 1001 (nine).

1. 7 Binary Codes (10 -24) Decimal Arithmetic Addition for signed numbers Apply 10‘s complement to the negative number only. Addition is done by summing all digits, including the sign digit, and discarding the end carry. Example (+375) + (- 240) (+0 375) + (9 760) = ( 1135) (end carry is discarded) = (0 135) in BCD

1. 7 Binary Codes (11 -24) Decimal Arithmetic Subtraction For BOTH signed and unsigned numbers: Apply 10‘s complement to the subtrahend apply addition (same as binary case)

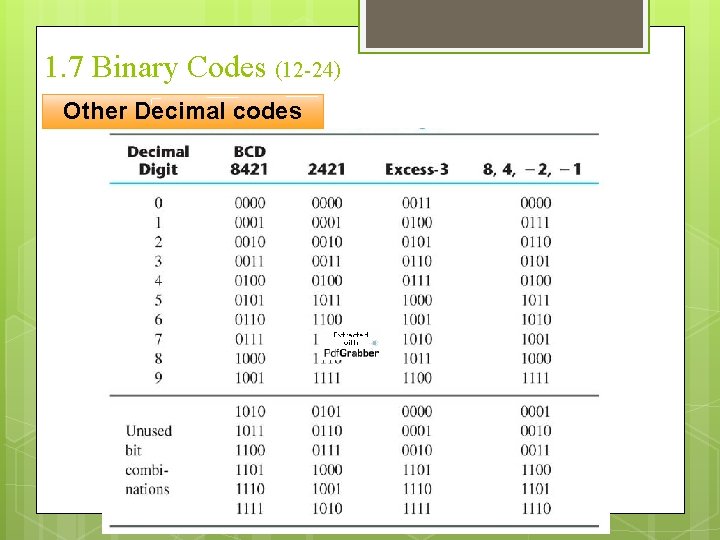
1. 7 Binary Codes (12 -24) Other Decimal codes

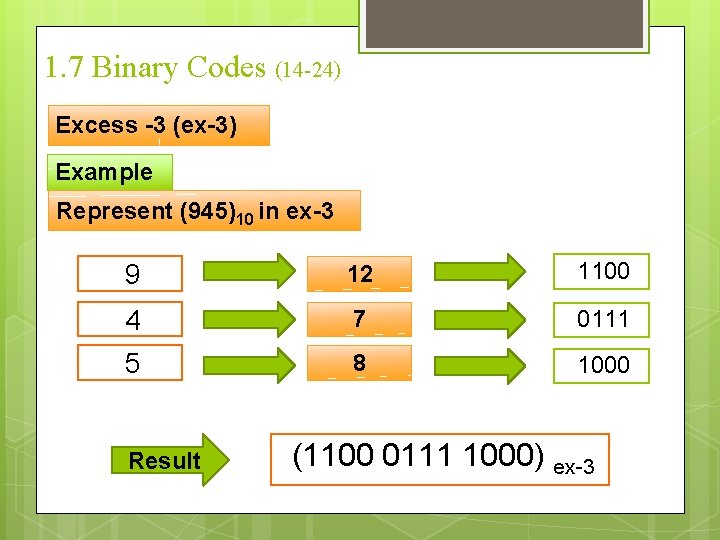
1. 7 Binary Codes (13 -24) Excess -3 (ex-3) Another system to represent a decimal number. Like (BCD) in the way of representing number (each digit is represented in 4 bits) Except that : each digit is firstly incremented by three

1. 7 Binary Codes (14 -24) Excess -3 (ex-3) Example Represent (945)10 in ex-3 9 12 1100 4 7 0111 5 8 1000 Result (1100 0111 1000) ex-3

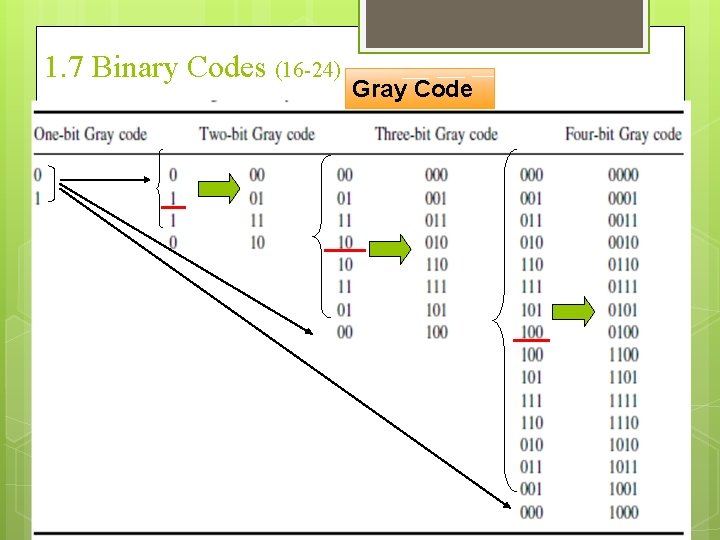
1. 7 Binary Codes (15 -24) Gray Code Output data of many physical systems are quantities that are continuous. Such data must be converted into digital form before they are applied to a digital system using analog-to-digital converter. Such converted data represented using Gray code. Used in applications in which the normal sequence of binary numbers may produce an error or ambiguity during the transition from one number to the next. Because only 1 bit in the code group changes in going from one number to the next.

1. 7 Binary Codes (16 -24) Gray Code

1. 7 Binary Codes (17 -24) Gray Code

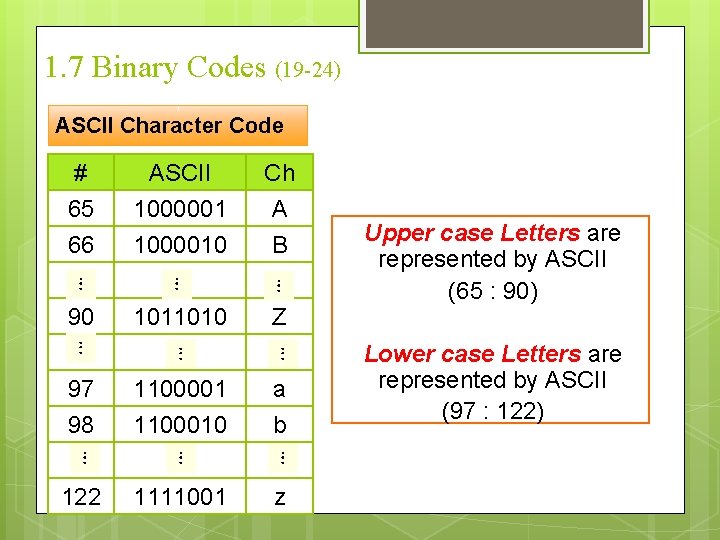
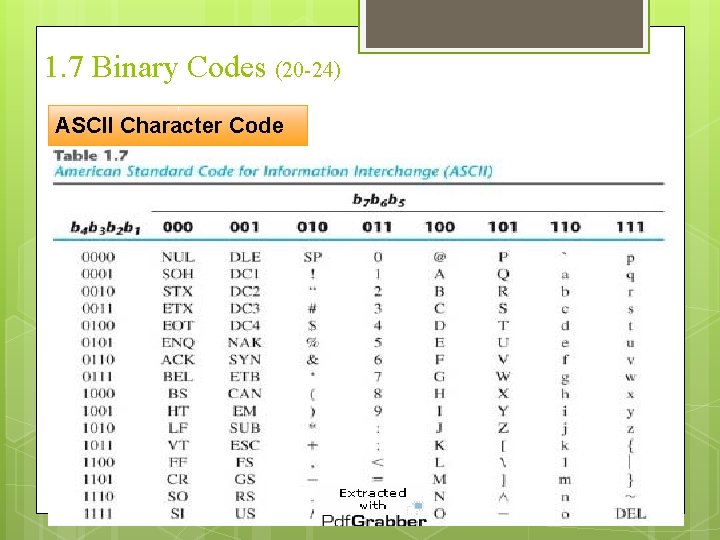
1. 7 Binary Codes (18 -24) ASCII Character Code ASCII : American Standard Code for Information Interchange Used to represent characters , Symbols , … Consists of 7 -bits (to represent 128 character). A bit can be added to produce a total of eight bits (byte). Used for other purposes.

1. 7 Binary Codes (19 -24) ASCII Character Code # 65 66 ASCII 1000001 1000010 Ch A B 90 1011010 Z 97 98 1100001 1100010 a b 122 1111001 z Upper case Letters are represented by ASCII (65 : 90) Lower case Letters are represented by ASCII (97 : 122)

1. 7 Binary Codes (20 -24) ASCII Character Code

1. 7 Binary Codes (21 -24) ASCII Character Code

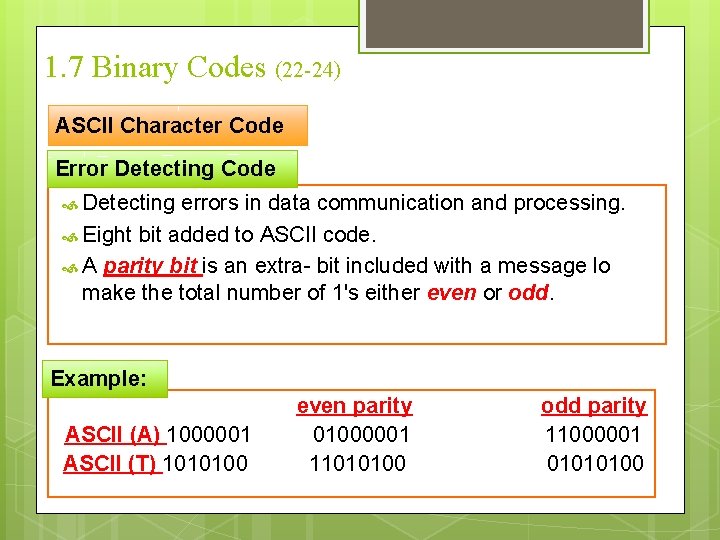
1. 7 Binary Codes (22 -24) ASCII Character Code Error Detecting Code Detecting errors in data communication and processing. Eight bit added to ASCII code. A parity bit is an extra- bit included with a message lo make the total number of 1's either even or odd. Example: even parity odd parity ASCII (A) 1000001 01000001 11000001 ASCII (T) 1010100 11010100 01010100

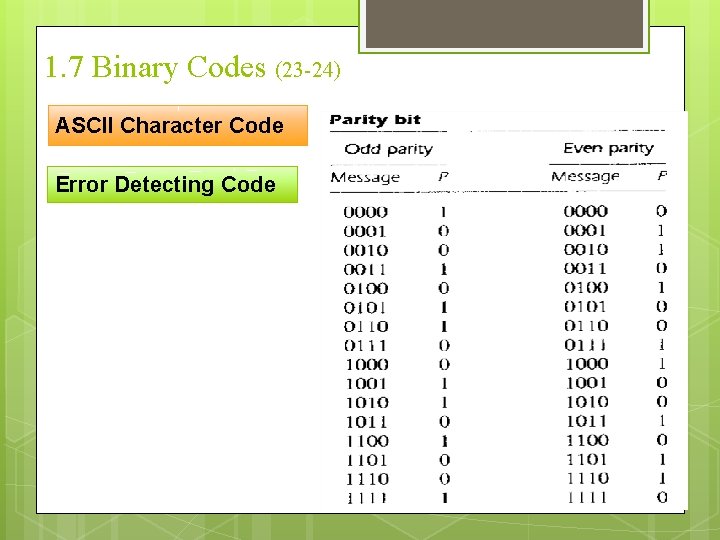
1. 7 Binary Codes (23 -24) ASCII Character Code Error Detecting Code

1. 7 Binary Codes (24 -24) ASCII Character Code Error Detecting Code The eight-bit character that include parity bits are transmitted to their destination. The parity of each character is then checked at the receiving end. If the parity of the received character is not even. then at least one bit has changed value during transmission. Detects one, three or any odd combination of errors in each character that is transmitted. Other detection codes may be needed to take care of that possibility