PHY 042 Electricity and Magnetism Vector calculus review

PHY 042: Electricity and Magnetism Vector calculus: review Prof. Hugo Beauchemin

Introduction to vector calculus v The aim of the course is to understand Maxwell’s equations v Start with their mathematical structures v Need to understand: v What vectors are, v Differentiation of vectors fields, v Integration of vector fields, v How to exploit symmetries of a system to simplify the formalization of a problem, v Theorems about vector fields.

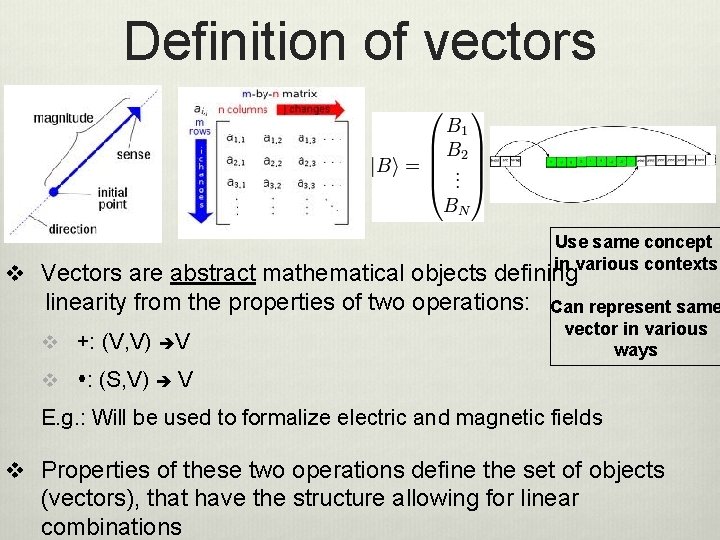
Definition of vectors Use same concept in various contexts v Vectors are abstract mathematical objects defining linearity from the properties of two operations: v +: (V, V) V v : (S, V) Can represent same vector in various ways V E. g. : Will be used to formalize electric and magnetic fields v Properties of these two operations define the set of objects (vectors), that have the structure allowing for linear combinations

Representation of vectors v A subset of all vectors of a given kind can be used to provide a unique decomposition for any other vector of that kind Basis of a vector space v It can serve as a references for representing a vector in a convenient coordinate system v Orthonormal basis v Spectral decomposition v The laws of physics must be independent of the choice of the coordinate system (same physics for any observer) v Will exploit this requirement to formulate problems in the coordinate system that is the most convenient

Special vector functions v Two special functions of vectors (taking two vectors as input): v Dot or Scalar product: : (V, V) S v Geometrical interpretation: projection of a vector on another one v E. g. : The components of a vector on the basis of a vector space v Allow to define the norm of a vector v Cross or Vector product: ×: (V, V) V v Geometrical interpretation: area of a parallelogram v Allow to define the determinant of a matrix v Will use the determinant to compute cross product! v Don’t forget the Right-hand rule!!! v Since the cross product yields a vector, we can define two different triple products: v Dot product with a cross product v Cross product with a cross product

Derivative v Vectors and vector fields can vary in space and in time v Each component can be a function of x, y, z and t v E. g. : v We can differentiate vectors. This changes both the norm and the direction of the vector v If we differentiate E with respect to t, then each scalar functions Ex, Ey and Ez will change, and thus the norm and the direction of the vector field E will change v We know how to differentiate multivariate scalar functions v This is vector laden!

Gradient v The variation of f between 2 nearby points (x, y, z) and (x’, y’. z’) is the scalar product of the gradient of f with the displacement vector between these nearby points v To be able to differentiate a function, a norm must be defined on the vector space v The gradient is a vector v It has a norm and a direction v Interpretation: v Point in direction of biggest increase of f (x, y, z) v Its norm gives the rate of the increase along the largest increase direction v Null variation of df: v Equipotential v Stationary points

Differential Operator v Recall: vectors are not arrows but abstract entities satisfying linearity operations We can define a vector differential operator: v Define vector differential operator in 3 D as: o Is there a difference between and ? Q: Why do we speak of a “vector operator”? A: It is an object that acts differently on each component of a vector to transform these components according to a well defined operation. Allows to define the derivative of multivariate vector fields!

Divergence v The divergence of a vector field is a scalar! v It is a number telling how much a vector is spreading out from a point, i. e. how much the lines of the field diverge from this point Note: These are not picture of the divergence of a field but picture of fields with different divergences.

Curl v The curl of a vector field is a vector! v The norm tells you how much the field is curling around an axis at a given point v The direction tells you around which axis the original field is curling v Use the right-hand rule to get this axis

Sum and product rules v Sum rule: The derivative of a sum of vector is given by the sum of the derivative of the elements of the sum v Thanks to the linearity of the vector differential operator and of the vectors summed v Product rule: many possibilities v v The product of two functions (vector or scalar) to be differentiated can be: v Scalar: or v Vector: or The derivative of a scalar function is a vector v Gradient v The derivative of a vector function is a: v Scalar: the divergence v Vector: the curl

Second derivative v Equation with 2 nd derivative are often used in physics v Field equations in function of potential such as Poisson v Characterize an extremum v There are 5 possibilities of second derivative Divergence Gradient of a scalar Vector Curl Divergence of a vector Scalar Curl of a vector Vector Gradient Divergence Curl

Integral vector calculus I v Problem to solve: v We want to perform definite integrals (integrals with specific boundary conditions) of vector fields Generalize the Fundamental Theorem of Calculus (FTC) v Boundaries: v The boundaries a and b enclose, limit, the integral interval. If the integral cover many dimensions (or just 1 D but embedded in an higher dimensional space), boundaries can be defined as: v Line (path) integral v Surface integral v Volume integral

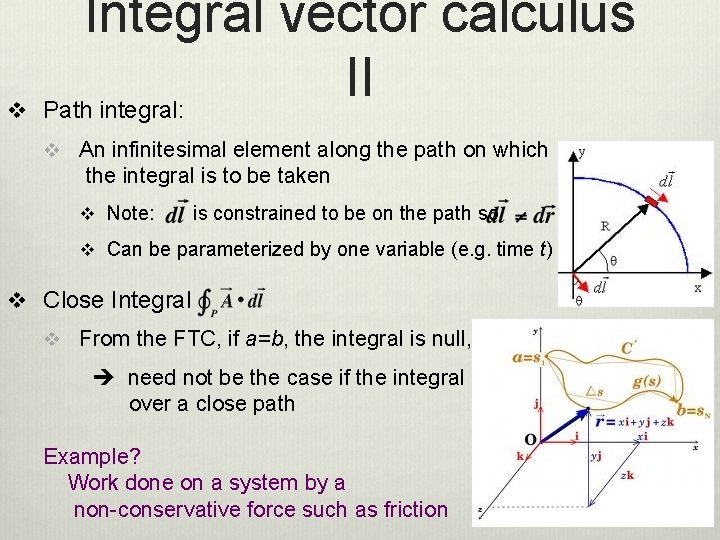
v Integral vector calculus II Path integral: v An infinitesimal element along the path on which the integral is to be taken v Note: is constrained to be on the path so v Can be parameterized by one variable (e. g. time t) v Close Integral v From the FTC, if a=b, the integral is null, need not be the case if the integral is over a close path Example? Work done on a system by a non-conservative force such as friction

Integral over a path (1 D) v To integrate a vector function over a given path P, we need: 1. Parameterize the path as a 1 variable function 2. Project the vector function onto the path 3. Integrate the product Only the lines of field along the path matter A B Only the components of field parallel to the path matter

Conservative forces v A force is conservative if the work it does along a path P is independent of that path, and only depends on the starting and ending points (path integral of F just depends on a and b) v If the vector field to integrate is a gradient, then this vector field describes a conservative force v This is just a special case of vector function Conservative -Independent of P -W=W’ -E. g. Falling stone Non-Conservative -Depends on P -W≠W’ -E. g. Pushing a box on the ground P P’

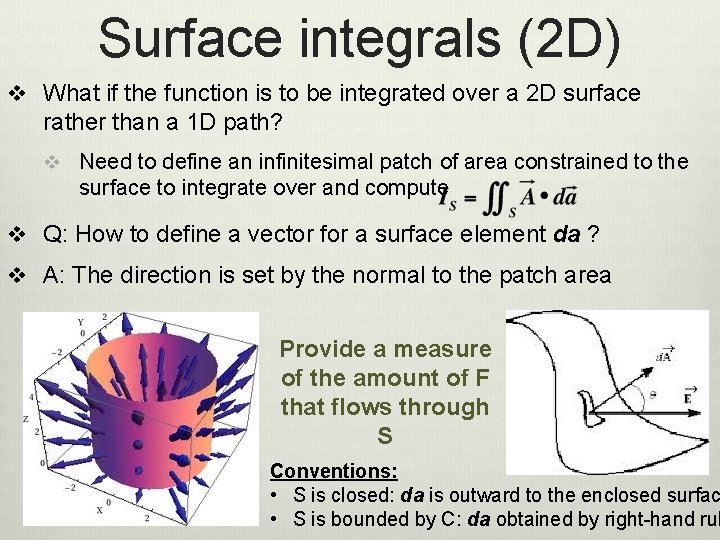
Surface integrals (2 D) v What if the function is to be integrated over a 2 D surface rather than a 1 D path? v Need to define an infinitesimal patch of area constrained to the surface to integrate over and compute v Q: How to define a vector for a surface element da ? v A: The direction is set by the normal to the patch area Provide a measure of the amount of F that flows through S Conventions: • S is closed: da is outward to the enclosed surfac • S is bounded by C: da obtained by right-hand rul

A question: Q: What is the difference between the circulation of a vector field and the flux of the vector field , i. e. the difference between and when the surface S is formed by a closed curve C? A: The circulation is the integration of the tangential component of the vector field on C and the flux is the integral of the normal component to C.

v Flux-divergence theorem I claimed in intro that the formulation of Maxwell’s equations in terms of curl and divergences are equivalent to their formulation in terms of flux and circulation v This is established by theorems v Flux-divergence (a. k. a. Gauss or Green theorem): v The integral of a derivative over a volume is equal to the primitive at the boundary, i. e. the whole surface enclosing that volume Measure of the outgoing divergence of a field from a point per unit volume Flux across a surface

Stokes theorem v Another version of the fundamental theorem of calculus: v The integral of a derivative over a surface is equal to its primitive at the boundary of the surface, i. e. over the circulation enclosing the surface Measure of the total amount of “swirl” of a vector field inside an area S Circulation of the field at the boundary

Spherical coordinates v Vectors are independent of coordinates (same vectors in different bases) v Can exploit the symmetry of a system to simplify the problem v The price to pay is to have a reference system that changes from point to point in the space

Cylindrical coordinates v Useful when you have a field generated by a wire, or by a solenoid for example v ATLAS/CMS detectors have cylindrical symmetry Like spherical coordinates but with

Helmholtz theorem v Generally, in E&M, we don’t know what the electric and magnetic fields are, but we know how they vary v Differential equations (Maxwell’s equation) v Is the divergence and the curl of a vector field determine the field at every point of space where these derivatives are defined and known? v Thm: A field is uniquely determined by its divergence, its curl (in a finite volume) and its boundary conditions Charge source Current source E&M: Use experiments to find relationships between sources and field variations

Potentials v Under certain conditions, fields can be obtained from the knowledge of the variation of underlying functions called potentials v Theorem 1: If the curl of a vector field is null: The circulation of the field over a closed path is null v The field is a conservative force v The field can be expressed as the gradient of a scalar potential v v Theorem 2: If the divergence of a field is null: The flux is null over a closed surface v The field can be expressed as the curl of a vector potential v For ANY field (always!):