Periodic driving forces Principle of Superposition Particular solution

Periodic driving forces • Principle of Superposition – Particular solution for a sum of cosine waves • Fourier Series – Periodic functions • The fundamental frequency – Orthogonal functions – Obtaining Fourier coefficients • Analogy with vector components • Fourier Series examples – The square wave – The saw tooth wave 1

What will we do in this chapter? We will consider the problem of driving a damped harmonic oscillator with a periodic but non-sinusoidal driving force. A periodic driving force has the property that f(t + t) = f(t) where t is the period. This is an interesting problem , but more importantly, it provides a great excuse for discussing the Fourier series. We begin by discussion the principle of superposition which is true for linear systems which obey linear differential equations. This allows us to obtain particular integrals for sums of sinusoidal driving forces. We next develop the technique of Fourier Series where we can write any periodic function of as a sum of sine and cosine functions with frequencies which are integral multiples of the fundamental frequency of w=2 p/t. Our demonstration exploits the fact that sine and cosine function are orthogonal functions which means that integral over the trig functions over a complete period vanishes unless they have are the same w multiple. There is analogy between finding Fourier components and vector components. We conclude by finding Fourier series for square and saw tooth waves. 2

Superposition Although this allows us to generalize the result quite a bit, it seems just like a curiosity, it can’t really be true that many periodic forces can be written as a sum of sinusoidal terms? But interestingly enough it is due to the Fourier Theorem 3

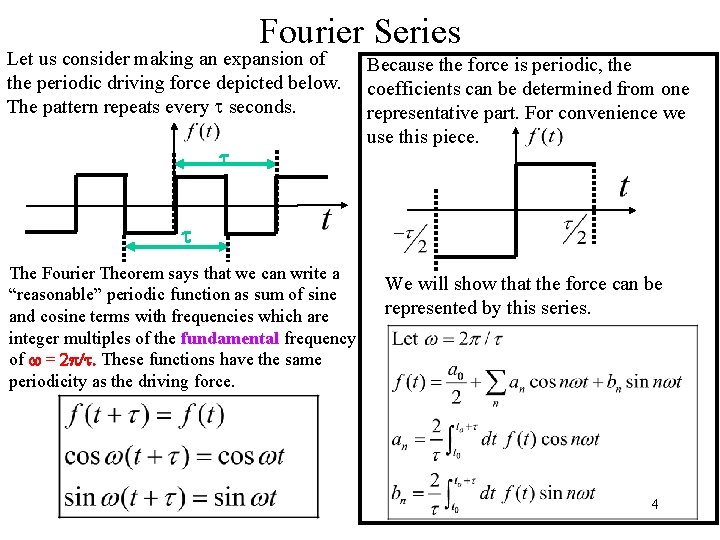
Fourier Series Let us consider making an expansion of the periodic driving force depicted below. The pattern repeats every t seconds. t Because the force is periodic, the coefficients can be determined from one representative part. For convenience we use this piece. t The Fourier Theorem says that we can write a “reasonable” periodic function as sum of sine and cosine terms with frequencies which are integer multiples of the fundamental frequency of w = 2 p/t. These functions have the same periodicity as the driving force. We will show that the force can be represented by this series. 4

Orthogonal functions We will show to get the coefficients an and bn which we will call the Fourier coefficients. The trick is to exploit an orthogonality property of the sin and cosine functions. If we integrate over one complete or multiple complete periods of the cosine curve we will get zero. This will happen for both terms as long as n and m are not equal or both equal to zero. 5

Orthogonal functions continued What happens when the trig integrals do not vanish? This vanishes for any integral trig argument since one always integrates over a full multiple of a sine oscillation. 6

Obtaining Fourier coefficients We thus can get the Fourier sine coefficients by integrating over one period with the sine of the given frequency. 7

Completing the coefficients This is a very deep analogy in linear 8 algebra called Hilbert Space

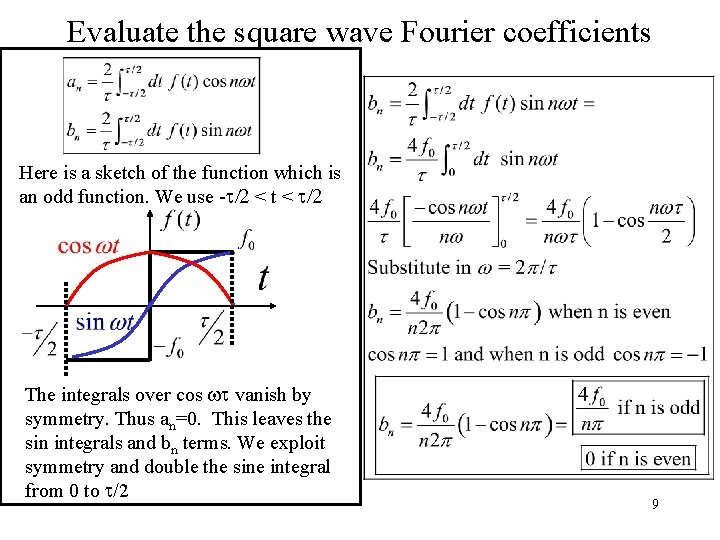
Evaluate the square wave Fourier coefficients Here is a sketch of the function which is an odd function. We use -t/2 < t/2 The integrals over cos wt vanish by symmetry. Thus an=0. This leaves the sin integrals and bn terms. We exploit symmetry and double the sine integral from 0 to t/2 9

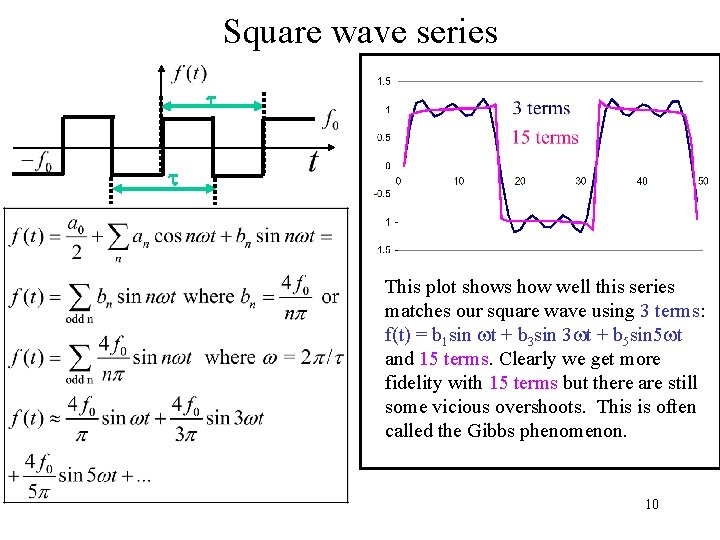
Square wave series t t This plot shows how well this series matches our square wave using 3 terms: f(t) = b 1 sin wt + b 3 sin 3 wt + b 5 sin 5 wt and 15 terms. Clearly we get more fidelity with 15 terms but there are still some vicious overshoots. This is often called the Gibbs phenomenon. 10

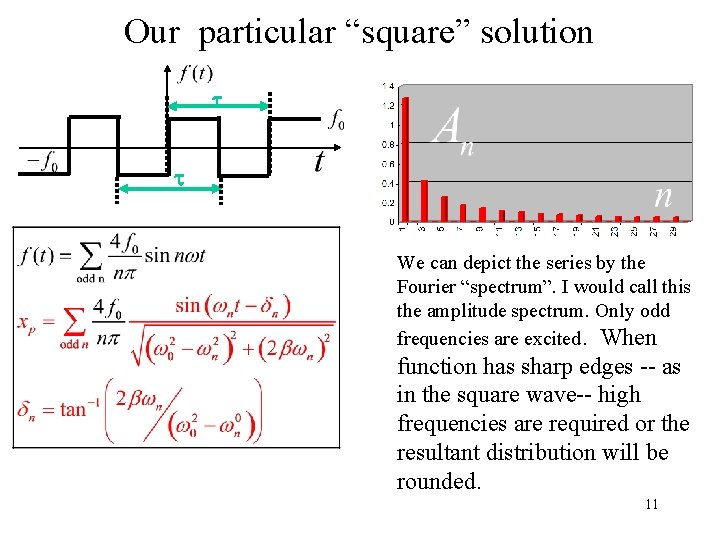
Our particular “square” solution t t We can depict the series by the Fourier “spectrum”. I would call this the amplitude spectrum. Only odd frequencies are excited. When function has sharp edges -- as in the square wave-- high frequencies are required or the resultant distribution will be rounded. 11

How to find a Fourier Series 12

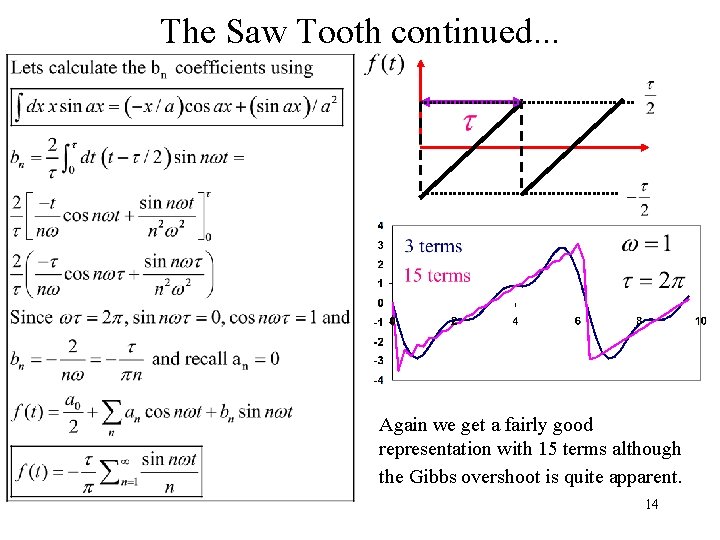
Saw tooth wave example This function is neither even or odd about t=0 so we will have both sin and cosine terms. We begin by evaluating the an cosine terms. This time we integrate from 0 to t rather than -t/2 to t/2 as we did last time. We actually get no cosine terms even though the saw tooth has mixed symmetry. This is actually because all cosine functions are even about t/2 and the saw tooth is odd about this point, but you can always work it out the hard way as we did. On to the sine coefficients. . 13

The Saw Tooth continued. . . Again we get a fairly good representation with 15 terms although the Gibbs overshoot is quite apparent. 14

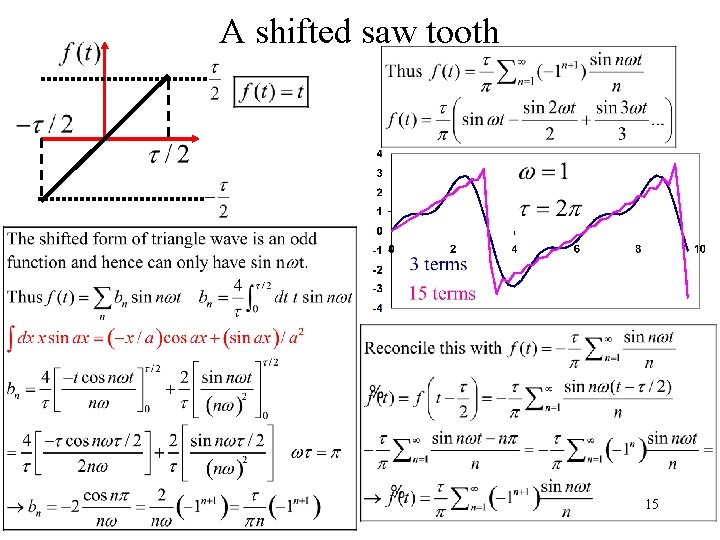
A shifted saw tooth 15