Pcsi Tudomnyegyetem Pollack Mihly Mszaki Kar Mszaki Informatika

Pécsi Tudományegyetem Pollack Mihály Műszaki Kar Műszaki Informatika Szak Data Mining 25. Előadás Dr. Pauler Gábor, Egyetemi Docens PTE-PMMFK Villamos Intézet Számítástechnika Tanszék Iroda: Boszorkány u. , B épület 101 Tel: 72/503 -650/3725 E-mail: gjpauler@acsu. buffalo. edu

Az előadás tartalma Egészértékű programozás • A korlátozás-szétválasztás algoritmusa Nemlineáris programozás • A nemlineáris modellek megoldásának bonyolultsága • Nemlineáris modellek linearizálása – Szakaszonként lineáris függvények linearizálása – Egyszerű nemlináris függvények linearizálása – HA-AKKOR szabályok kezelése lineáris modellben – Logikai kapcsolatok leírása bináris változókkal – Bonyolultabb nemlineáris célfüggvények linearizálása • Hiperbolikus programozás • Befektetési alap kezelési probléma • Dinamikus programozás Szakirodalom

LP modellek egészértékű döntési változókkal 1 A gyakorlatban sok problémában fordulnak elő diszkrét értékű döntési változók (Discrete Variables), amelyeknek csak véges vagy végtelen számú diszkrét értéke értelmezett (pl. oszthatatlan termékek, nem gyárthatunk 23. 5 db repülőgépet). • Ezek a leggyakrabban egészértékű változóként (Integer Variable) jelennek meg, egészértékű LP modellt (Integer LP, ILP model) eredményezve • Ezek speciális esete a bináris {0, 1} változók (Binary LP, BLP model) használata, ezek általában nemlineáris modellek linearizálásakor kerülnek elő A simplex algoritmus viszont a sztenderd LP modellben csak folytonos változókat képes kezelni, és az optimális megoldás is bármikor lehet tört értékű • Kézenfekvő dolognak látszik, hogy az egészértékű optimális megoldáshoz kerekítsük a folytonos optimális megoldást • Ez azonban csak akkor működik jól, ha az egészértékű változó egysége csak elenyészően kis részét fogyasztja el a kapacitásoknak (pl. Fradi meccs elött a zacskóba töltendő szotyolamagok számát nyugodtan kerekíthetjük) • Más a helyzet, ha az egészértékű változó egysége a kapacitások jelentős részét elfogyasztja (pl. az építendő óceánjárók számának optimalizálása). Itt a folytonos eredmény egyszerű kerekítése már lehet, hogy nem megengedett megoldás, vagy pedig, nagyon messze fog esni az optimálistól.

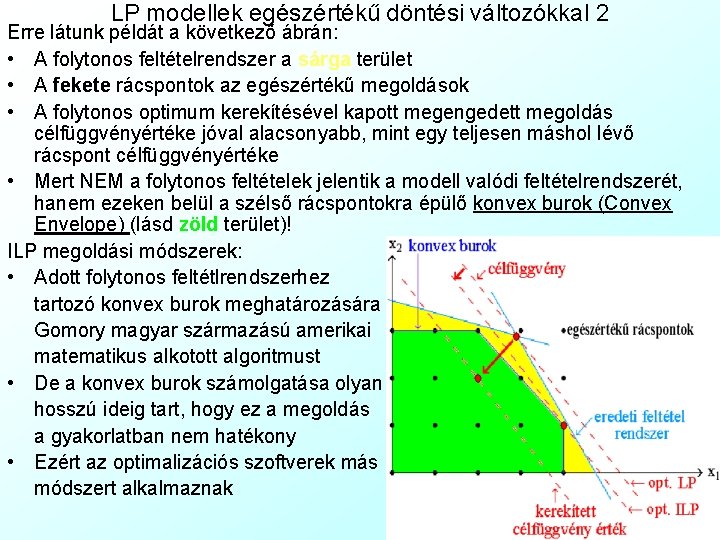
LP modellek egészértékű döntési változókkal 2 Erre látunk példát a következő ábrán: • A folytonos feltételrendszer a sárga terület • A fekete rácspontok az egészértékű megoldások • A folytonos optimum kerekítésével kapott megengedett megoldás célfüggvényértéke jóval alacsonyabb, mint egy teljesen máshol lévő rácspont célfüggvényértéke • Mert NEM a folytonos feltételek jelentik a modell valódi feltételrendszerét, hanem ezeken belül a szélső rácspontokra épülő konvex burok (Convex Envelope) (lásd zöld terület)! ILP megoldási módszerek: • Adott folytonos feltétlrendszerhez tartozó konvex burok meghatározására Gomory magyar származású amerikai matematikus alkotott algoritmust • De a konvex burok számolgatása olyan hosszú ideig tart, hogy ez a megoldás a gyakorlatban nem hatékony • Ezért az optimalizációs szoftverek más módszert alkalmaznak

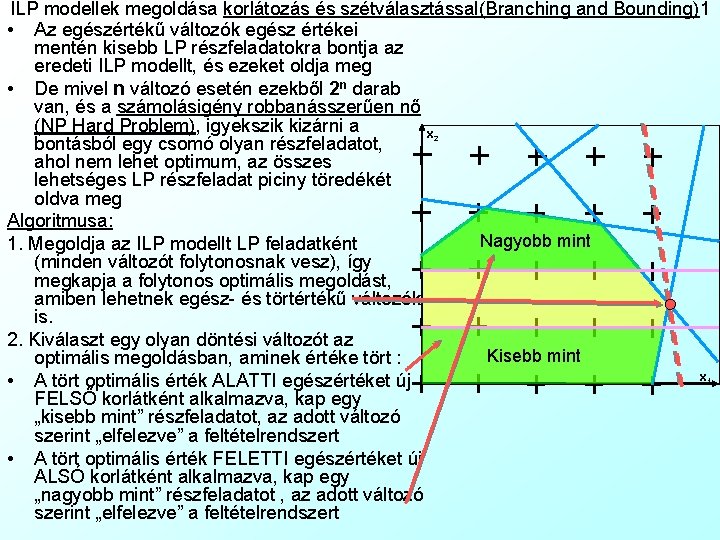
ILP modellek megoldása korlátozás és szétválasztással(Branching and Bounding)1 • Az egészértékű változók egész értékei mentén kisebb LP részfeladatokra bontja az eredeti ILP modellt, és ezeket oldja meg • De mivel n változó esetén ezekből 2 n darab van, és a számolásigény robbanásszerűen nő (NP Hard Problem), igyekszik kizárni a x 2 bontásból egy csomó olyan részfeladatot, ahol nem lehet optimum, az összes lehetséges LP részfeladat piciny töredékét oldva meg Algoritmusa: Nagyobb mint 1. Megoldja az ILP modellt LP feladatként (minden változót folytonosnak vesz), így megkapja a folytonos optimális megoldást, amiben lehetnek egész- és törtértékű változók is. 2. Kiválaszt egy olyan döntési változót az Kisebb mint optimális megoldásban, aminek értéke tört : x 1 • A tört optimális érték ALATTI egészértéket új FELSŐ korlátként alkalmazva, kap egy „kisebb mint” részfeladatot, az adott változó szerint „elfelezve” a feltételrendszert • A tört optimális érték FELETTI egészértéket új ALSÓ korlátként alkalmazva, kap egy „nagyobb mint” részfeladatot , az adott változó szerint „elfelezve” a feltételrendszert

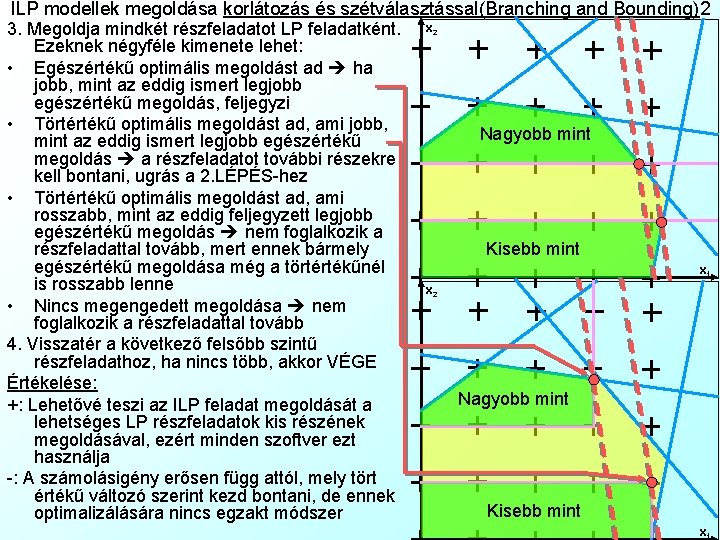
ILP modellek megoldása korlátozás és szétválasztással(Branching and Bounding)2 3. Megoldja mindkét részfeladatot LP feladatként. Ezeknek négyféle kimenete lehet: • Egészértékű optimális megoldást ad ha jobb, mint az eddig ismert legjobb egészértékű megoldás, feljegyzi • Törtértékű optimális megoldást ad, ami jobb, mint az eddig ismert legjobb egészértékű megoldás a részfeladatot további részekre kell bontani, ugrás a 2. LÉPÉS-hez • Törtértékű optimális megoldást ad, ami rosszabb, mint az eddig feljegyzett legjobb egészértékű megoldás nem foglalkozik a részfeladattal tovább, mert ennek bármely egészértékű megoldása még a törtértékűnél is rosszabb lenne • Nincs megengedett megoldása nem foglalkozik a részfeladattal tovább 4. Visszatér a következő felsőbb szintű részfeladathoz, ha nincs több, akkor VÉGE Értékelése: +: Lehetővé teszi az ILP feladat megoldását a lehetséges LP részfeladatok kis részének megoldásával, ezért minden szoftver ezt használja -: A számolásigény erősen függ attól, mely tört értékű változó szerint kezd bontani, de ennek optimalizálására nincs egzakt módszer x 2 Nagyobb mint Kisebb mint x 1

Az előadás tartalma Egészértékű programozás • A korlátozás-szétválasztás algoritmusa Nemlineáris programozás • A nemlineáris modellek megoldásának bonyolultsága • Nemlineáris modellek linearizálása – Szakaszonként lineáris függvények linearizálása – Egyszerű nemlináris függvények linearizálása – HA-AKKOR szabályok kezelése lineáris modellben – Logikai kapcsolatok leírása bináris változókkal – Bonyolultabb nemlineáris célfüggvények linearizálása • Hiperbolikus programozás • Befektetési alap kezelési probléma • Dinamikus programozás Szakirodalom

Nemlineáris Programozás • Nemlineáris programozás (Nonlinear Programming, NLP) esetén a célfüggvény vagy a feltételek linearitása nem teljesül Az NLP modell megoldásának a nehézségét a következők határozzák meg: • A célfüggvény és a feltételek konkavitása/konvexitása: – Konvex (Convex) egy függvény, ha a • • A szélsőérték fajtája konvex feltételrendszernél: – Konvex célfüggvénynek csak egy globális Minimalizálás • x x Maximalizálás függvényfelület bármely két pontját összekötő szakasz a függvényfelületen vagy felette helyezkedik el – Konkáv (Concave), ha alatta – Ha egyik sem igaz a függvény teljes értelmezési tartományán, akkor az sem konkáv sem konvex (pl. y = x 3, stb. ) y y minimuma lehet, de sok lokális maximuma – Konkáv célfüggvénynek csak egy globális maximuma lehet, de sok lokális minimuma Konkáv feltételrendszer esetén több lokális Konvex célfüggvény Konkáv célfüggvény szélsőérték lehetséges bármely célfüggvénynél • A legnehezebben megoldható általános NLP A lokális szélsőértékek nehezítik a megoldást, modelleknél a célfüggvény vagy a feltételek sem mert az algoritmusok „beléjük ragadhatnak” konvexek sem konkávak

Szakaszonként lineáris függvények kezelése 1 Könnyen kezelhető esetek: • Szakaszonként lineáris konvex összefüggés minimalizálása (pl. L túlóra emelkedő költségei: c 1 ≤ c 2 ≤ c 3) – Plussz változók bevezetése: L felbontása L 1+L 2+L 3 szakasz változókra – Szakasz-határ korlátok bevezetése: L 1’, L 2’, L 3’ c 1 L 1 + c 2 L 2 + c 3 L 3 = z → Min (25. 1) L 1 ≤ L 1 ’ (25. 2) L 2 ≤ L 2 ’ - L 1 ’ (25. 3) L 3 ≤ L 3 ’ - L 2 ’ (25. 4) L 1 + L 2 + L 3 - L = 0 (25. 5) L 1 , L 2 , L 3 , L ≥ 0 (25. 6) • Szakaszonként lineáris konkáv összefüggés maximalizálása (pl. Q értékesítés mennyiségi árengedménnyel: p 1 ≥ p 2 ≥ p 3) – Plussz változók bevezetése: Q felbontása Q 1+Q 2+Q 3 szakasz változókra – Szakasz-határ korlátok bevezetése: Q 1’, Q 2’, Q 3’ p 1 Q 1 + p 2 Q 2 + p 3 Q 3 = z → Max (25. 7) Q 1 ≤ Q 1 ’ (25. 8) Q 2 ≤ Q 2 ’ - Q 1 ’ (25. 9) Q 3 ≤ Q 3 ’ - Q 2 ’ (25. 10) Q 1 + Q 2 + Q 3 - Q = 0 (25. 11) Q 1 , Q 2 , Q 3 , Q ≥ 0 (25. 12)

Szakaszonként lineáris függvények kezelése 2 Nehezen kezelhető esetek: Szakaszonként lineáris konvex függvény maximalizálása, konkáv minimalizálása, nem konkáv/konvex függvény kezelése (pl. sin(y), cos(y) közelítése): – Kiszámítjuk az f(d 0), . . f(d 4) függvényérték pontokat d 0, . . d 4 tetszőleges osztópontokban – Az eredeti y változót az osztópontok 0, . . 4 ≥ 0 nemnegatív súly változókkal súlyozott összegeként írjuk fel: d 0 0 + d 1 1 + d 2 2 + d 3 3 + d 4 4 – y = 0 (25. 13) – Az függvényértéket a függvényérték pontok hasonlóan súlyozott összegeként írjuk fel: f(d 0) 0 + f(d 1) 1 + f(d 2) 2 + f(d 3) 3 + f(d 4) 4 (25. 14) – Hogy ne kelljen a súlyok összegével osztani, legyen az összegük 1: 0 + 1 + 2 + 3 + 4 = 1 (25. 15) – Hogy a súlyok CSAK a szomszédos függvénypontok közti szakaszokat ábrázolhassák, egyszerre csak két szomszédos súly kaphat nem 0 értéket – Ezt úgy érjük el, hogy az x 1, . . x 4 є {0, 1} szomszédságot ábrázoló bináris változókat teszünk a súlyok felső korlátjává. Mivel a közbülső súlyoknak két szomszédja is lehet, ezért ezeknél két szomszédsági változó összege lesz a korlát: 0 x 1 (25. 16) - egy szomszédja van 1 x 1+x 2 (25. 17) - két szomszédja van 2 x 2+x 3 (25. 18) - két szomszédja van 3 x 3+x 4 (25. 19) - két szomszédja van 4 x 4 (25. 20) - egy szomszédja van – Egyszerre csak egy szomszédság „működhet”, ezért a szomsédság jelölő változók összege legyen 1: x 1 +x 2 +x 3 + x 4 = 1 (25. 21)

Az előadás tartalma Egészértékű programozás • A korlátozás-szétválasztás algoritmusa Nemlineáris programozás • A nemlineáris modellek megoldásának bonyolultsága • Nemlineáris modellek linearizálása – Szakaszonként lineáris függvények linearizálása – Egyszerű nemlináris függvények linearizálása – HA-AKKOR szabályok kezelése lineáris modellben – Logikai kapcsolatok leírása bináris változókkal – Bonyolultabb nemlineáris célfüggvények linearizálása • Hiperbolikus programozás • Befektetési alap kezelési probléma • Dinamikus programozás Szakirodalom

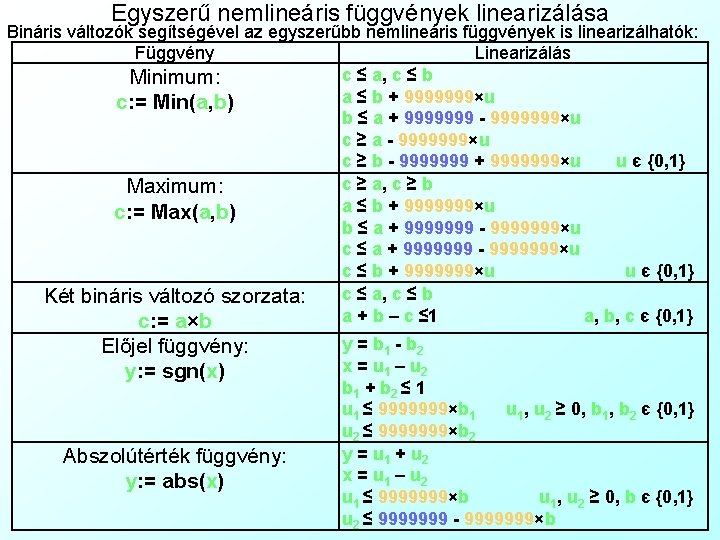
Egyszerű nemlineáris függvények linearizálása Bináris változók segítségével az egyszerűbb nemlineáris függvények is linearizálhatók: Függvény Linearizálás c ≤ a, c ≤ b Minimum: a ≤ b + 9999999×u c: = Min(a, b) b ≤ a + 9999999 - 9999999×u c ≥ a - 9999999×u c ≥ b - 9999999 + 9999999×u u є {0, 1} c ≥ a, c ≥ b Maximum: a ≤ b + 9999999×u c: = Max(a, b) b ≤ a + 9999999 - 9999999×u c ≤ b + 9999999×u u є {0, 1} c ≤ a, c ≤ b Két bináris változó szorzata: a + b – c ≤ 1 a, b, c є {0, 1} c: = a×b Előjel függvény: y: = sgn(x) Abszolútérték függvény: y: = abs(x) y = b 1 - b 2 x = u 1 – u 2 b 1 + b 2 ≤ 1 u 1 ≤ 9999999×b 1 u 1, u 2 ≥ 0, b 1, b 2 є {0, 1} u 2 ≤ 9999999×b 2 y = u 1 + u 2 x = u 1 – u 2 u 1 ≤ 9999999×b u 1, u 2 ≥ 0, b є {0, 1} u 2 ≤ 9999999 - 9999999×b

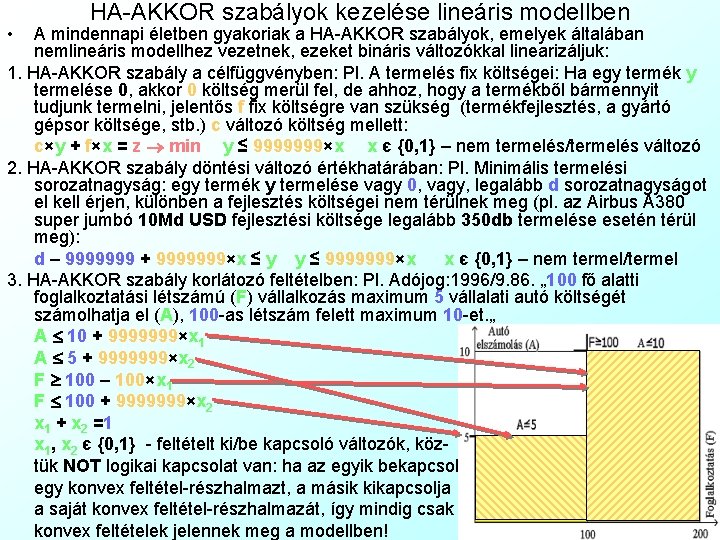
• HA-AKKOR szabályok kezelése lineáris modellben A mindennapi életben gyakoriak a HA-AKKOR szabályok, emelyek általában nemlineáris modellhez vezetnek, ezeket bináris változókkal linearizáljuk: 1. HA-AKKOR szabály a célfüggvényben: Pl. A termelés fix költségei: Ha egy termék y termelése 0, akkor 0 költség merül fel, de ahhoz, hogy a termékből bármennyit tudjunk termelni, jelentős f fix költségre van szükség (termékfejlesztés, a gyártó gépsor költsége, stb. ) c változó költség mellett: c×y + f×x = z min y ≤ 9999999×x x є {0, 1} – nem termelés/termelés változó 2. HA-AKKOR szabály döntési változó értékhatárában: Pl. Minimális termelési sorozatnagyság: egy termék y termelése vagy 0, vagy, legalább d sorozatnagyságot el kell érjen, különben a fejlesztés költségei nem térülnek meg (pl. az Airbus A 380 super jumbó 10 Md USD fejlesztési költsége legalább 350 db termelése esetén térül meg): d – 9999999 + 9999999×x ≤ y y ≤ 9999999×x x є {0, 1} – nem termel/termel 3. HA-AKKOR szabály korlátozó feltételben: Pl. Adójog: 1996/9. 86. „ 100 fő alatti foglalkoztatási létszámú (F) vállalkozás maximum 5 vállalati autó költségét számolhatja el (A), 100 -as létszám felett maximum 10 -et. „ A 10 + 9999999×x 1 A 5 + 9999999×x 2 F 100 – 100×x 1 F 100 + 9999999×x 2 x 1 + x 2 =1 x 1, x 2 є {0, 1} - feltételt ki/be kapcsoló változók, köztük NOT logikai kapcsolat van: ha az egyik bekapcsol egy konvex feltétel-részhalmazt, a másik kikapcsolja a saját konvex feltétel-részhalmazát, így mindig csak konvex feltételek jelennek meg a modellben!

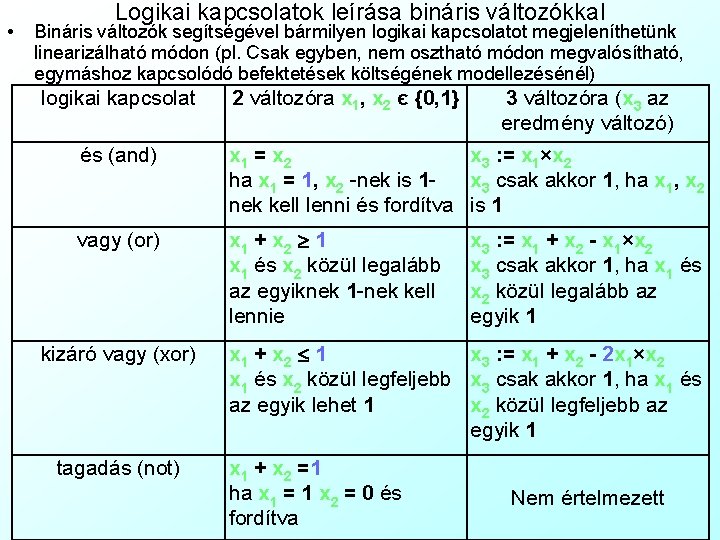
• Logikai kapcsolatok leírása bináris változókkal Bináris változók segítségével bármilyen logikai kapcsolatot megjeleníthetünk linearizálható módon (pl. Csak egyben, nem osztható módon megvalósítható, egymáshoz kapcsolódó befektetések költségének modellezésénél) logikai kapcsolat 2 változóra x 1, x 2 є {0, 1} 3 változóra (x 3 az eredmény változó) és (and) x 1 = x 2 x 3 : = x 1×x 2 ha x 1 = 1, x 2 -nek is 1 x 3 csak akkor 1, ha x 1, x 2 nek kell lenni és fordítva is 1 vagy (or) x 1 + x 2 1 x 1 és x 2 közül legalább az egyiknek 1 -nek kell lennie kizáró vagy (xor) tagadás (not) x 3 : = x 1 + x 2 - x 1×x 2 x 3 csak akkor 1, ha x 1 és x 2 közül legalább az egyik 1 x 1 + x 2 1 x 3 : = x 1 + x 2 - 2 x 1×x 2 x 1 és x 2 közül legfeljebb x 3 csak akkor 1, ha x 1 és az egyik lehet 1 x 2 közül legfeljebb az egyik 1 x 1 + x 2 =1 ha x 1 = 1 x 2 = 0 és fordítva Nem értelmezett

Az előadás tartalma Egészértékű programozás • A korlátozás-szétválasztás algoritmusa Nemlineáris programozás • A nemlineáris modellek megoldásának bonyolultsága • Nemlineáris modellek linearizálása – Szakaszonként lineáris függvények linearizálása – Egyszerű nemlináris függvények linearizálása – HA-AKKOR szabályok kezelése lineáris modellben – Logikai kapcsolatok leírása bináris változókkal – Bonyolultabb nemlineáris célfüggvények linearizálása • Hiperbolikus programozás • Befektetési alap kezelési probléma • Dinamikus programozás Szakirodalom

Bonyolultabb nemlineáris célfüggvények linearizálása 2 Hiperbolikus célfüggvény (Hyperbolic Programming, HP): pl. i = 1. . n termékek xi termeléseinek Scixi összköltségre jutó Spixi összbevételét akarjuk maximalizálni (termelés profitabilitásának maximalizálása) a célfüggvény egy tört lesz: • • (25. 30) Alapfeltételezések: a nevező pozitív, a kapcsolódó feltételrendszer lineáris, konvex: c 1 x 1 + c 2 x 2 + r > 0 a 1 x 1 + a 2 x 2 ≤ b (25. 31) Linearizáció: mikor nem számít a célfüggvényt nem lineárissá tévő osztás? – Ha pontosan 1 -el osztunk. Legyen u≥ 0 egy változó, amivel a nevezőt megszorozva az értéke pontosan 1 lesz (ez implicite kizárja u = 0 -át is): p c 1 x 1 u + c 2 x 2 u + ru = 1 (25. 32) x 2 – Hogy a z célfüggvény ne változzon, u-val végigszorozzuk a számlálót is: z p 1 x 1 u + p 2 x 2 u + qu = z Max (25. 33) – Ugyanezt megtehetjük a feltételeknél is, anélkül, hogy az értelmük megváltozna: a 1 x 1 u + a 2 x 2 u ≤ bu (25. 34) Az eredeti xi i = 1. . n változók u-val alkotott szorzatát lecseréljük yi = xi × u, i = 1. . n változókra: p 1 y 1 + p 2 y 2 + qu = z Max (25. 35) (q, r) c 1 y 1 + c 2 y 2 + ru = 1 (25. 36) c a 1 y 1 + a 2 y 2 - bu ≤ 0 (25. 37) x 1 y 1, y 2, u ≥ 0 (25. 38) Megoldjuk a lineáris modellt, hogy megkapjuk az (yi* i = 1. . n, u*) optimális megoldást. Majd u*-gal történő osztással megkapjuk az eredeti változók szerinti optimális megoldást: xi* = yi* / u*, i = 1. . n (25. 39)

• Bonyolultabb nemlineáris célfüggvények linearizálása 3 Az exponenciális-, haranggörbe-, bevételi görbe-, logisztikus függvények linearizálását már tárgyaltuk a Session 15 -ben. Lássunk ezek használatára egy példát: 25. 1. PÉLDA: Befektetési alap kezelési modell (Found Management Model): • Egy befektetési alapkezelő k nagyú tőkét kamatoztat t = 1. . T időperióduson keresztül i = 1. . n befektetési lehetőségben, amelyek éves szintű reálkamatlábai ri, si időperiódusoktól kezdve elérhetőek, lejárati időtartamuk di (ha a lejárati időt megszakítjuk, elvesztjük a kamatokat). • Mely befektetési lehetőségeket válasszuk (bi {0, 1}), hogy a T időperióduson keresztül elérhető z jövőbeli érték maximális legyen? • Az ilyen modelleknél rendkívül hasznos, ha minden t kamatperiódusú (pl. t=1 éves, t=12 havi) rt reálkamatlábat átváltunk f folytonos kamatlábra (Continuos Interest Rate), amely egy valóságban sohasem létező, fiktív kamatláb: az eredeti befektetéssel egyenértékű olyan befektetés kamatlába, amely végtelenül rövid lejárati idejű és azonnal újrabefektethető: f = t × ln(1 + rt/t) (25. 40) • Így a modellben nem kell folyton átváltogatnunk a különböző kamatperiódusú kamatlábakat egymásba, és egy t időperiódusnyi lejáratú befektetés z jövőbeli értéke rendkívül egyszerűen, jól linearizálhatóan számolható: z = k × eft (25. 41) • Ha szükséges, az f folytonos kamatláb bármikor visszaváltható adott kamatperiódusú rt reálkamatlábba: rt = t × (ef/t - 1) (25. 42)

Bonyolultabb nemlineáris célfüggvények linearizálása 4 Célfüggvény: k × e(Sifidibi) = z Max /Maximális jövőbeli érték (25. 43) Subject to bi {0, 1}, i = 1. . n /Bináris befektetési változók (25. 44) bi + bj ≤ 1, i, j = 1. . n| ((si ≤ sj)AND(sj ≤ si+di))OR((sj ≤ si)AND(si ≤ sj+dj)) /Nem valósulhat meg egyszerre két beruházás, amelyek lejárati intervallumai átfedik egymást (25. 45) • A modell célfüggvénye nemlineáris, de rendkívül egyszerűen loglinearizálható egy ekvivalens lineáris célfüggvénybe: ln(k) + Sifidibi = ln(z) Max /Max. jövőbeli érték logaritmusa (25. 46) • A fentiekből láthattuk, hogy a lineáris programozásban nem a linearitás jelenti a fő gondot, mert szinte mindent linearizálni lehet • Azonban, minél bonyolultabb egy linearizálás, annál inkább megtöbbszörözi a feltételek és a (gyakran egészértékű) változók számát a modellben • 30 -40 változós nemlineáris problémákból simán létrejöhetnek több 10000 változós, jelentős részben egészértékű modellek, ami olyan óriási számolásigényt jelent, ami – mégha szuperszámítógépi kapacitás és idő birtokában megoldható is – gazdaságtalanná teszi a probléma megoldását • De van egy trükk, ami jelentősen csökkentheti a modellek méretét, és további linearizálási lehetőséget jelent:

Dinamikus programozás 1 A dinamikus programozás (Dynamic Programming, DP) olyan modellek optimalizálásával foglalkozik, amelyeknél • a döntési változók és a korlátozó feltételek azonos szerkezetű csoportjai minden egymást követő időperiódusban megjelennek • az időperiódusok láncszerűen hatnak egymásra: az előző periódus eredményei a következő periódus bemenetei lesznek • A modellt egy időbeli ablakban (Time Window) írjuk fel • Lássunk erre egy példát: 25. 2 PÉLDA: A Kobe-i kikötőöbölben található a világ leghosszabb kétpilléres függőhídja, erősen ciklonveszélyes területen. Az erős szél hatására a hídpálya lengésbe jön, és az aktuális terheléstől is függő, időben szinuszos hullámmozgást ír le. • A híd leszakadását egy automatika akadályozza meg, amely hatalmas hidraulikák segítségével periodikusan megfeszíti/ellazítja a híd tartókábeleit, csillapítva a hullámzást. Jelenítsük meg egy LP modellben korlátként a hullámmozgás at amplitúdóját t = 1. . T időperiódusok és a w aktuális terhelés szerint (lásd a mellékelt függvényt), hogy a hidraulikák húzó/nyomó igénybevétele (h, n) tervezhető legyen!

Dinamikus programozás 2 • Ha ezt a brutálisan nemlineáris, bonyolult függvényt az előzőekben mutatott szakaszonként lineáris felbontás módszerével szeretnénk megjeleníteni, folytonos súlyvátozók, szomszédsági változók és feltételek ezreire lenne szükség. • Ha azonban a modellt dinamikusan írjuk fel, aszerint, hogy bizonyos előző időperiódusok hogyan hatnak a következő időperiódusban, akkor: • Eleve változókat takaritunk meg, mert a függvényt nem a teljes időtartamban kell ábrázolni, hanem egy szűk időbeli ablakban • A Session 15 -ben az autoregressziós modelleknél tanultak alapján kihasználhatjuk, hogy egy szinuszos hullámzást időszeletek szintjén lineárisan is közelíteni lehet, ezért a feltétel megjelenítése egyszerűsödik: at = +0. 355×at-1 – 0. 650×at-6, t = 7. . T (25. 47) a 1 = -w, a 2 = -w, a 3 = -w (25. 48) a 4 = -w, a 5 = -w, a 6 = -w (25. 49) h ≤ at, n ≥ - at , t = 1. . T (25. 50)

Szakirodalom 1 Egészértékű programozás: • Gömöry algoritmus: http: //www. inf. u-szeged. hu/~pluhar/oktatas/or 2. pdf • Korlátozás és szétválasztás: www. oplab. sztaki. hu/szem_20050506. doc Nemlineáris programozás: • Kvadratikus programozás: www. oplab. sztaki. hu/szem_20050318. doc • Hiperbolikus programozás: www. freeweb. hu/szmulai/files/ elsoevf/gazdmattetel. doc • Dinamikus programozás: www. mimi. hu/informatika/programozas. html Lineáris programozás modell könyvtárak: • Gams Inc. : http: //www. gams. com/modlib/libhtml/subindx. htm • Optimax Inc. : http: //www. maximal-usa. com/ • Frontline Inc. : http: //www. solver. com/sdkplatform. htm • Brunel: http: //people. brunel. ac. uk/~mastjjb/jeb/or/lp. html Áttekintés az optimalizációs algoritmusokról szoftverekről: • http: //www-fp. mcs. anl. gov/otc/Guide/Software. Guide/Categories/linearprog. html Ingyenes lineáris optimalizációs szoftverek: • Dream: http: //sourceforge. net/projects/dr-ea-m • HQP: http: //sourceforge. net/projects/hqp • OCC: http: //sourceforge. net/projects/occ

Szakirodalom 2 Kereskedelmi optimalizációs szoftverek: • Kiegészítések más rendszerekhez: –Matlab: nincs shareware http: //www. mathworks. com/products/optimization/ • Önálló rendszerek: –Gams: max. 100000 változó/feltétel, GUI, 300 változóra/feltételre korlátozott időkorlát nélküli shareware: http: //www. gams. com/ –LINDO Inc. LINGO: max. 100000 változó/feltétel, GUI, 300 változóra/feltétel korlátozott időkorlát nélküli shareware: http: //www. lindo. com/cgi/frameset. cgi? leftdwnld. html; opsyslgof. html –Cplex: http: //www. ilog. com/products/cplex/ –Gauss: http: //www. aptech. com/ • Excel add-in solverek: –LINDO Inc. What’s Best: max. 100000 változó, 300 változóra korlátozott időkorlát nélküli shareware: http: //www. lindo. com/cgi/frameset. cgi? leftdwnld. html; opsyswbf. html –Frontline Inc. Solver: max. 8000 változó, 30 napos shareware: http: //www. solver. com/exceluse. htm#Premium%20 Solver%20 Platform