Mszaki fizika alapjai Az anyagi pont dinamikja Dr

























- Slides: 33

Műszaki fizika alapjai Az anyagi pont dinamikája Dr. Giczi Ferenc Széchenyi István Egyetem, Fizika és Kémia Tanszék Győr, Egyetem tér 1. 1

Kérdések 1. 2. A testek mozgásánál más testeknek mi a szerepe? Van-e a mozgó testnek olyan tulajdonsága, amely a mozgás szempontjából lényeges? 2

A tehetetlenség törvénye Newton I. törvénye 1. A testek mozgásánál más testeknek mi a szerepe? Mindennapos tapasztalatok alapján: Minden test megmarad a nyugalom, vagy az egyenes vonalú egyenletes mozgás állapotában, míg más test hatásai állapotának megváltoztatására nem kényszerítik. Példák: 1. Elgurított golyó… 2. Induló, fékező vagy kanyarodó járművön álló utasok… 3. Köszörűkőről leváló darabok… 3

Milyen vonatkoztatási rendszerben igaz a tehetetlenség törvénye? Inerciarendszerben Tény, hogy van olyan vonatkoztatási rendszer, un. tehetetlenségi vagy inerciarendszer, amelyben a tehetetlenség törvénye érvényes. 4

A tehetetlenség Van-e a mozgó testnek olyan tulajdonsága, amely a mozgás szempontjából lényeges? Mindennapos tapasztalatok alapján: VAN, A TEHETETLENSÉGÜK. A tehetetlenség a testeknek az a tulajdonsága, hogy a sebességük megváltoztatására irányuló hatásoknak ellenszegülnek. 5

Erőhatás Newton I. törvénye alapján következik: Ha egy test inerciarendszerhez viszonyított sebessége változik (gyorsul), azt mindig más test hatásának kell tulajdonítani. A testeknek egy más testre gyakorolt olyan hatását, amely a test sebességének megváltozásában (gyorsulásában) nyilvánul meg, erőhatásnak, vagy röviden erőnek nevezzük. 6

Az erőnek egy testre gyakorolt hatását a test gyorsulásából ismerhetjük fel. Ezért fel kell tételezni, hogy az erő és a gyorsulás között kapcsolat van. Kísérleti tapasztalatok alapján: 1. Egy meghatározott testre ható erő annál nagyobb, minél nagyobb a test időegységre eső sebességváltozása (gyorsulása). - Az erőnek irányt is tulajdoníthatunk (a gyorsulás irányát). 2. Szerepe van egy a test tehetetlenségének mértékét kifejező mennyiségnek, a test tehetetlen tömegének 7

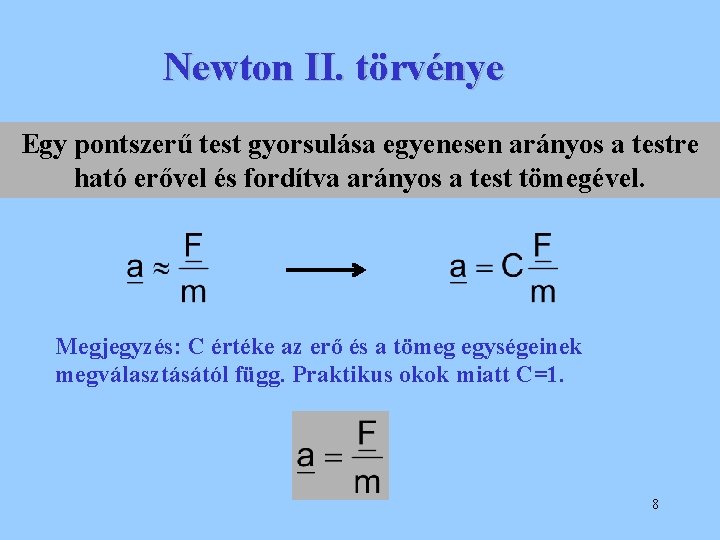
Newton II. törvénye Egy pontszerű test gyorsulása egyenesen arányos a testre ható erővel és fordítva arányos a test tömegével. Megjegyzés: C értéke az erő és a tömeg egységeinek megválasztásától függ. Praktikus okok miatt C=1. 8

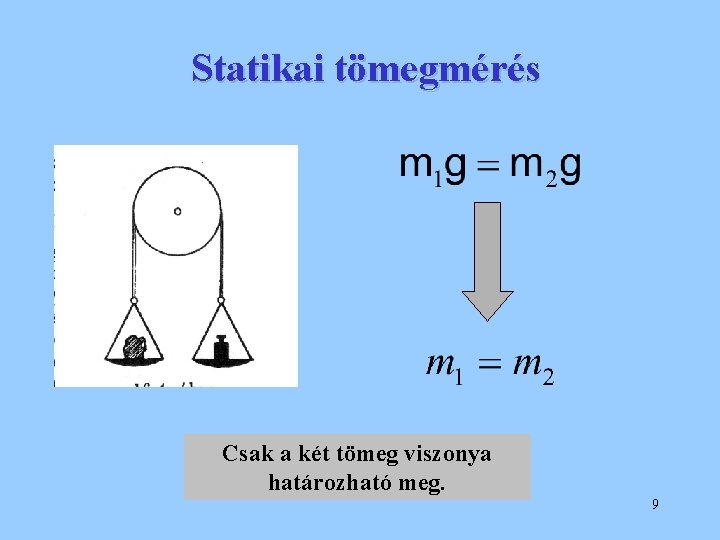
Statikai tömegmérés Csak a két tömeg viszonya határozható meg. 9

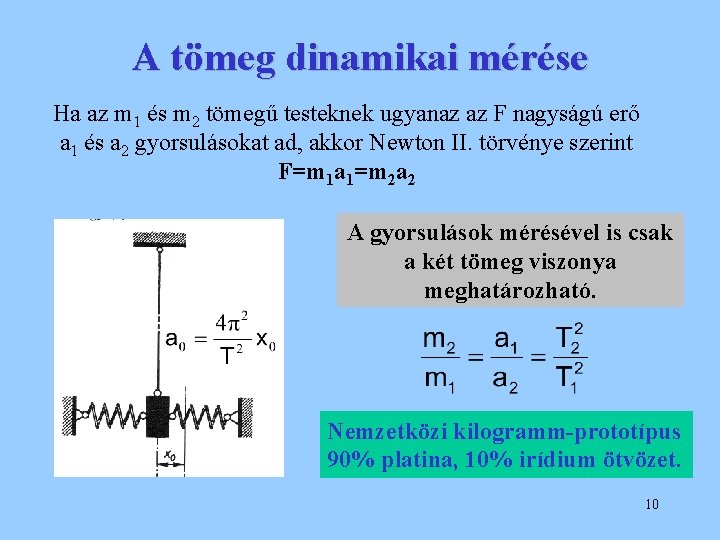
A tömeg dinamikai mérése Ha az m 1 és m 2 tömegű testeknek ugyanaz az F nagyságú erő a 1 és a 2 gyorsulásokat ad, akkor Newton II. törvénye szerint F=m 1 a 1=m 2 a 2 A gyorsulások mérésével is csak a két tömeg viszonya meghatározható. Nemzetközi kilogramm-prototípus 90% platina, 10% irídium ötvözet. 10

Az erő dinamikai mérése Az erőt a tömeg és a gyorsulás mérésével határozzuk meg az F=m a alapegyenlet segítségével. 1 newton (N) nagyságú az az erő, amelynek hatására 1 kg tömegű test 1 m/s 2 gyorsulással mozog. 11

Gyakorló feladat 1. Mekkora eredő erő hat az 50 kg tömegű testre, ha álló helyzetből indulva 2 m/s sebességet 1 m hosszon ér el? 2. Mekkora állandó erő hatására fékeződik le egy 0, 2 kg tömegű, 4 m/s sebességű test 10 s alatt? 12

A kölcsönhatás törvénye Newton III. törvénye Ha egy (pontszerű) A testre a (pontszerű) B test erőt fejt ki, akkor az A test is hat a B-re ugyanolyan nagyságú és ellentétes irányú erővel. 14

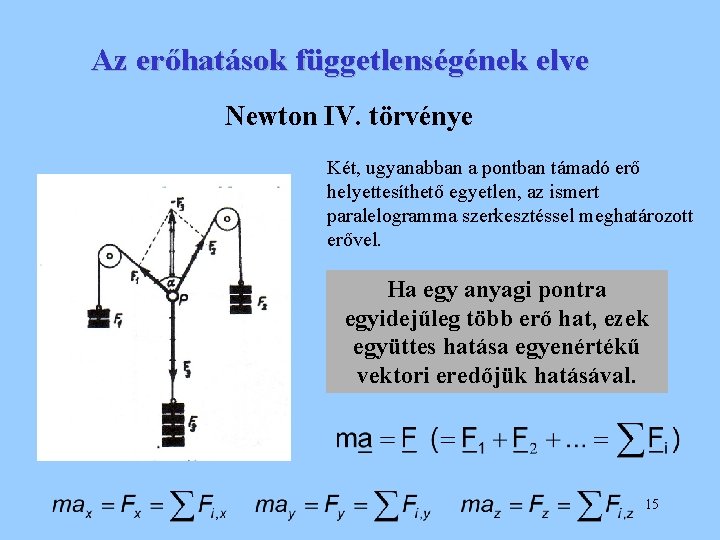
Az erőhatások függetlenségének elve Newton IV. törvénye Két, ugyanabban a pontban támadó erő helyettesíthető egyetlen, az ismert paralelogramma szerkesztéssel meghatározott erővel. Ha egy anyagi pontra egyidejűleg több erő hat, ezek együttes hatása egyenértékű vektori eredőjük hatásával. 15

A dinamika alapegyenlete Egy pontszerű test tömegének és (inerciarendszerre vonatkoztatott) gyorsulásának szorzata egyenlő a testre ható erők eredőjével. 16

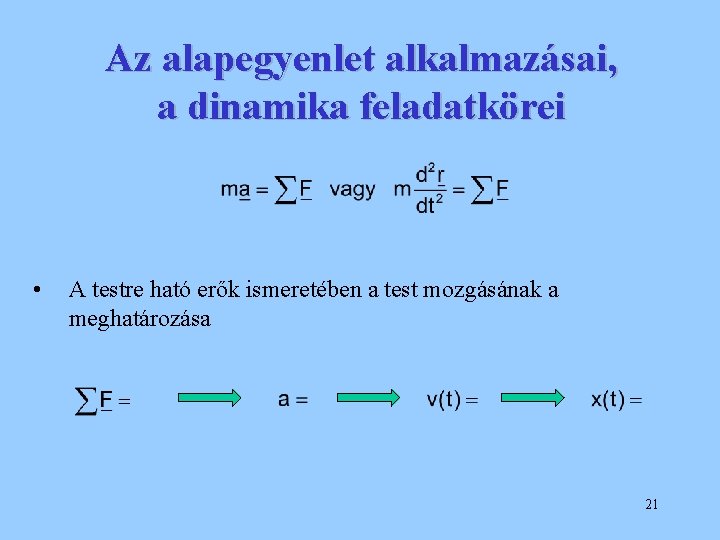
Az alapegyenlet alkalmazásai, a dinamika feladatkörei • A mozgások kísérleti vizsgálata alapján erőtörvények felállítása 17

Erőtörvények felállítása 1. A szabadon eső testek mozgására a g nehézségi gyorsulás a jellemző. Erőtörvény: 2. Az egyenes vonalú harmonikus rezgőmozgásokra Erőtörvény: 18

Erőtörvények felállítása 3. A bolygók mozgásának vizsgálata Erőtörvény: =6, 67 10 -11 Nm 2/kg 2 4. Egyéb erőtörvények: súrlódás, légellenállás, stb. 19

Gyakorló feladat A Föld sugara 6370 km. Mekkora az 1 kg tömegű testre ható vonzóerő 6370 km magasan a Föld felszíne felett? (A Föld tömege 6*1024 kg. =6, 67*10 -11 Nm 2/kg 2 ) 20

Az alapegyenlet alkalmazásai, a dinamika feladatkörei • A testre ható erők ismeretében a test mozgásának a meghatározása 21

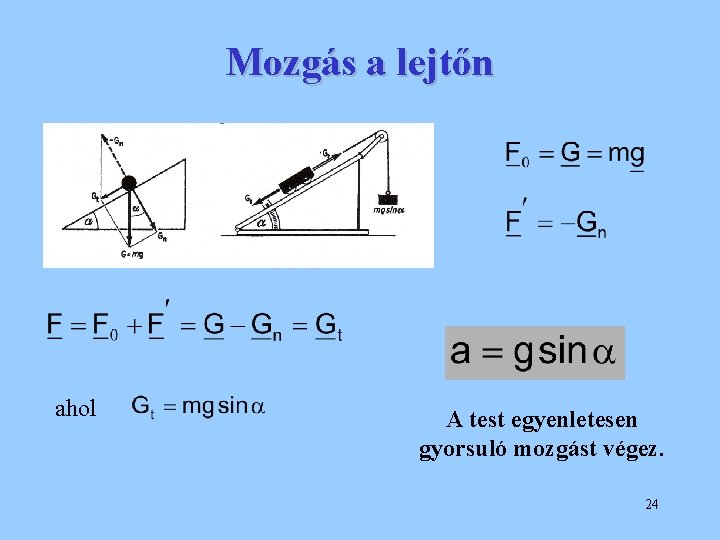
Kényszermozgások esetén a testnek előírt, merevnek tekinthető felületen vagy görbén kell maradnia. Szabad mozgások • hajítás • égitestek mozgása Kényszermozgások • mozgás a Föld felszínén • lejtőn történő mozgás • ingamozgás 22

A kényszermozgások dinamikai alapegyenlete F 0 a szabaderők, F’ a kényszererők eredője (A kényszererők általában nem ismertek, azonban a mozgás irányára mindig merőlegesek. ) 23

Mozgás a lejtőn ahol A test egyenletesen gyorsuló mozgást végez. 24

Gyakorló feladat Egy 300 -os hajlásszögű lejtőre fel akarunk húzni egy 40 kg tömegű testet egyenletes mozgással. Mekkora erőt kell alkalmazni, ha a súrlódás elhanyagolható? a. / Ha a lejtővel párhuzamos irányban húzzuk? b. / Ha vízszintes irányban húzzuk? 25

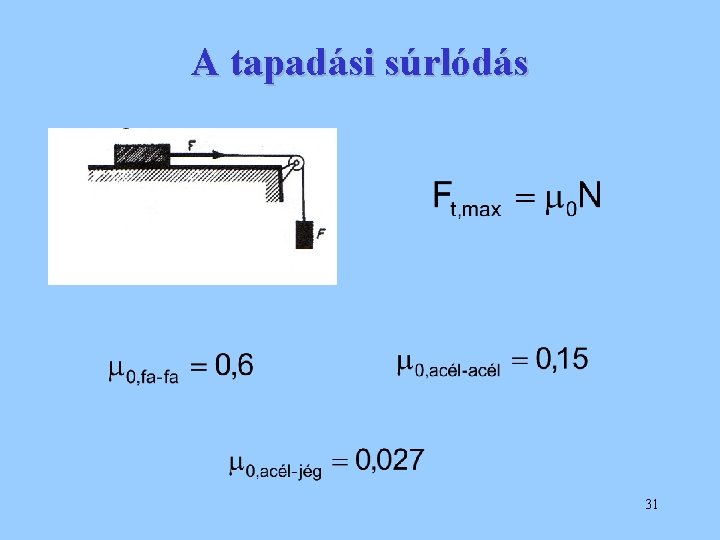
A csúszási súrlódás erőtörvénye: A sebességgel mindig ellentétes irányú súrlódási erő, nagysága első közelítésben független az érintkező felületeknek és a sebességnek a nagyságától, és arányos az N nyomóerővel. (Coulomb, 1736 -1806) 26

Gyakorló feladat Az 5 kg tömegű testet vízszintes talajon, vízszintes hatásvonalú 30 N állandó erővel húzunk. A test és a talaj között a súrlódási együttható 0, 4. Mekkora gyorsulással mozog a test? 27

A csúszási súrlódás lejtőn lecsúszó testre A test gyorsulás nélkül mozogna az olyan α hajlásszögű lejtőn, amelyre (Ennek alapján µ egyszerűen meghatározható. ) 28

Gyakorló feladat Egy 300 -os hajlásszögű lejtőn egy test mozog lefelé. a. / Mekkora a gyorsulása, ha a súrlódás elhanyagolható? b. / Mekkora a gyorsulás, ha a súrlódási együttható 0, 2? 29

Gyakorló feladat Egy 5 kg tömegű testet akarunk felhúzni a 60 m hosszú, 30 fokos hajlásszögű lejtőn. A test és a lejtő közötti csúszó súrlódási együttható 0, 3. Határozzuk meg azt a lejtővel párhuzamos erőt, amely a testet egyenletes mozgással húzza felfelé. 30

A tapadási súrlódás 31

Gyakorló feladat Egy teherautó tömege 2 t, sebessége 20 m/s. A rakománya és a rakodófelület közötti súrlódási együttható 0, 3. Mekkora fékezőerővel lehet a kocsit megállítani a rakomány megcsúszásának veszélye nélkül? Mekkora távon belül történik a megállás? 32

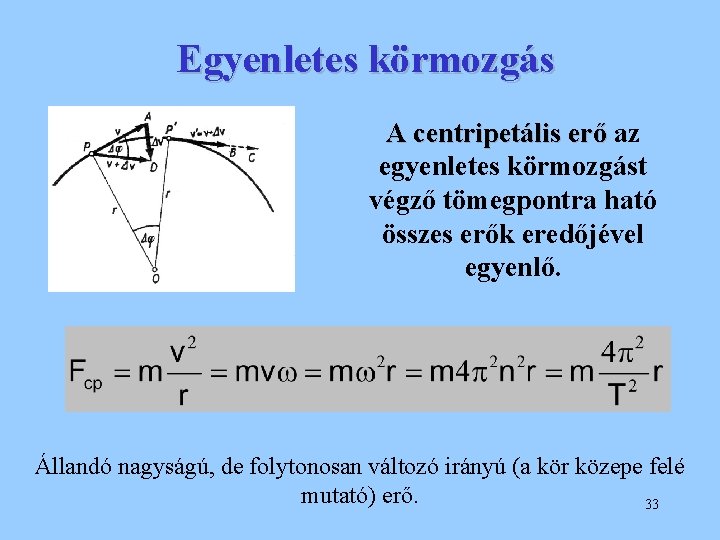
Egyenletes körmozgás A centripetális erő az egyenletes körmozgást végző tömegpontra ható összes erők eredőjével egyenlő. Állandó nagyságú, de folytonosan változó irányú (a kör közepe felé mutató) erő. 33

Gyakorló feladat Vízszintes, súrlódásmentes asztallapon 1 m hosszú fonal végén 2 kg tömegű golyó egyenletes körmozgást végez. Keringési ideje 1, 2 s. a. / Mekkora a golyó kerületi sebessége? b. / Mekkora erő feszíti a fonalat? 35