Optimality in strategic games CP nets and soft

Optimality in strategic games, CP nets and soft constraints

Main aim n n n To compare the notion of optimality used in many formalisms To throw the basis for exploiting results in one field and reuse them in the other field Strategic games q Agent interaction while pursuing their own interest (payoff function) CP nets q Agent’s qualitative and conditional preferences Soft constraints q Agent’s quantitative preferences

Outline 1. 2. 3. Strategic games Relation between CP nets and games Relation between soft constraints and games

Parametrized Strategic games n n A set of players 1, . . , n For each player i: q q n A set of strategies Si A strict total order >i over Si depending on s-i (a joint strategy of all players but player i): payoff function Example (prisoner’s dilemma): 2 players, 2 strategies (ci, ni) for each player i C 2 N 2 C 1 3, 3 0, 4 N 1 4, 0 1, 1

Pure Nash equilibria n n N 2 0, 4 N 1 4, 0 1, 1 A strategy si is a best response for i to s-i if si ≥i s’i for all s’i in Si A joint strategy s is a pure Nash equilibrium if each si is a best response to s-i q q q n C 1 C 2 3, 3 Also: for all i, for all s’i in Si, si ≥i s’i No player has regrets on the strategy he chose But there could be better joint strategies if more than one player changed its strategy In the example, one Nash equilibria (NE): (N 1, N 2)

Pareto efficient joint strategies n n No other joint strategy is better or equal for all agents, and better for at least one Example: q q (N 1, N 2): unique Nash equilibrium All other joint strategies are Pareto efficient (PE) C 2 N 2 C 1 3, 3 0, 4 N 1 4, 0 1, 1

Dominance between strategies n n A strategy si is never a best response for i if it is not a best response to any joint strategy s-i In the example: for each player i, Ci is never a best response C 2 N 2 C 1 3, 3 0, 4 N 1 4, 0 1, 1

Elimination of dominated strategies n G NBR G’ q q G’ subgame of G For all i, each si in Si-S’i is never a best response for i in G Eliminate from the strategies of each players those that are never a best response

Nash equilibria and strategy elimination n n If G NBR G’, then s Nash equilibrium of G iff Nash equilibrium of G’ In the example: Ci is nbr, thus G’ has one row and one column, which is the unique Nash equilibrium 1, 1 C 2 N 2 C 1 3, 3 0, 4 N 1 4, 0 1, 1

From CP-nets to games n Given a CP-net N, we build the game g(N) q q q Players: features Strategies of player i: domain of feature xi Payoff function of player i: CP table for xi n n Given s-i, s’i >i si iff s-i|par(xi) : s’i >i si in the cp table for variable i Thm: opt(N) = NE(g(N))

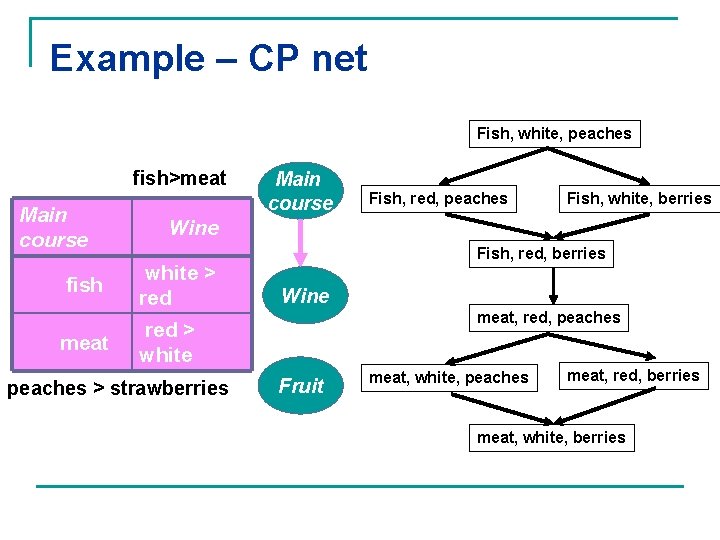
Example – CP net Fish, white, peaches fish>meat Main course fish meat Main course Fish, red, peaches Fish, white, berries Wine white > red Fish, red, berries Wine meat, red, peaches red > white peaches > strawberries Fruit meat, white, peaches meat, red, berries meat, white, berries

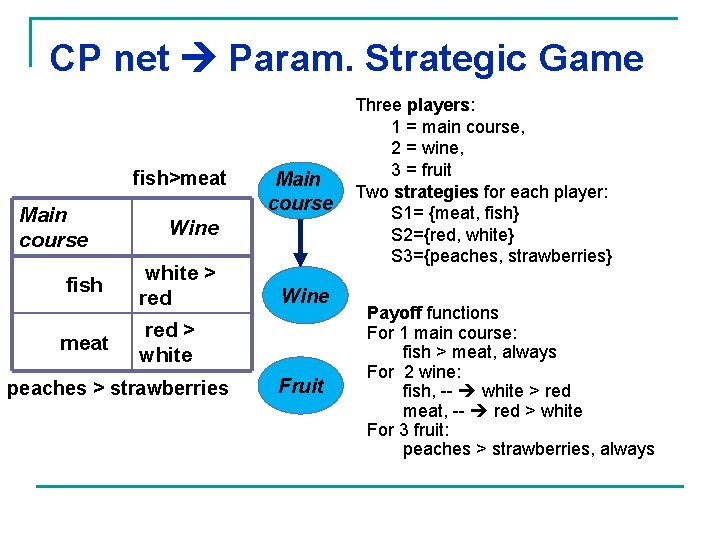
CP net Param. Strategic Game fish>meat Main course fish meat Main course Wine white > red Wine red > white peaches > strawberries Fruit Three players: 1 = main course, 2 = wine, 3 = fruit Two strategies for each player: S 1= {meat, fish} S 2={red, white} S 3={peaches, strawberries} Payoff functions For 1 main course: fish > meat, always For 2 wine: fish, -- white > red meat, -- red > white For 3 fruit: peaches > strawberries, always

Example: optimals and Nash equilibria n Unique optimal for CP-net: (fish, white, peaches) q n Hard constraints: fish, peaches, fish white, meat red For the game: q q Meat is nbr for main course Strawberries is nbr for fruit Once meat is eliminated, red is nbr for wine Nash equilibrium: fish, white, peaches

From games to CP-nets n Given a game G, we build a CP-net n(G): q q n Feature xi: player i Domain of xi: strategies for player i Parents of xi: all the other features CP table of xi: s-i: si > s’i if si >i s’i given s-i Thm. : NE(G) = opt(n(G))

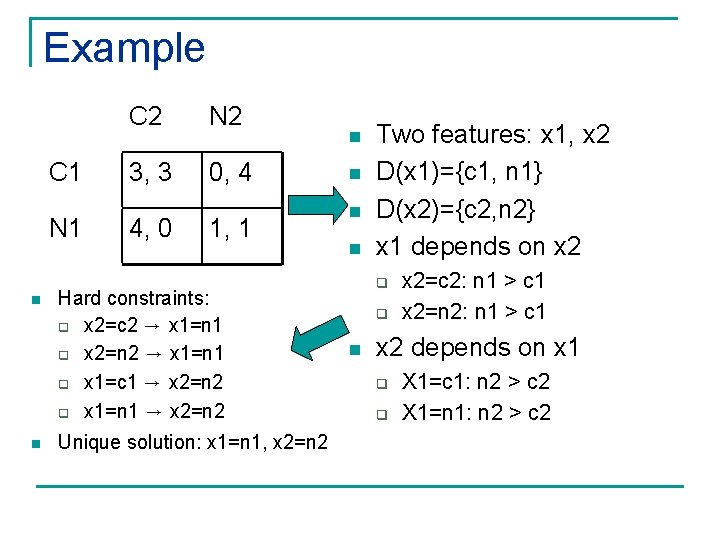
Example C 1 N 1 n n C 2 N 2 3, 3 0, 4 4, 0 1, 1 Hard constraints: q x 2=c 2 → x 1=n 1 q x 2=n 2 → x 1=n 1 q x 1=c 1 → x 2=n 2 q x 1=n 1 → x 2=n 2 Unique solution: x 1=n 1, x 2=n 2 n n Two features: x 1, x 2 D(x 1)={c 1, n 1} D(x 2)={c 2, n 2} x 1 depends on x 2 q q n x 2=c 2: n 1 > c 1 x 2=n 2: n 1 > c 1 x 2 depends on x 1 q q X 1=c 1: n 2 > c 2 X 1=n 1: n 2 > c 2

Reduced CP-nets n n If y is a parent of x, but the preference over the domain of x does not depend on y, then we can remove y from the parents of x eliminate rows From a CP net N to its reduced version r(N)

Example: reduced CP-net n n Two features: x 1, x 2 D(x 1)={c 1, n 1} D(x 2)={c 2, n 2} x 1 depends on x 2 q q n x 2=c 2: n 1 > c 1 x 2=n 2: n 1 > c 1 x 2 depends on x 1 q q X 1=c 1: n 2 > c 2 X 1=n 1: n 2 > c 2 n n n Two features: x 1, x 2 D(x 1)={c 1, n 1} D(x 2)={c 2, n 2} x 1 and x 2 independent For x 1: n 1 > c 1 For x 2: n 2 > c 2

CP-net techniques in games n n From game G to n(G) From n(G) to r(n(G)) Hard constraints for r(n(G)) Optimals of r(n(G)) = Nash equilibria of G G n n(G) r Nash equilibria of G = optimals of r(n(G))

Example C 1 N 1 C 2 N 2 3, 3 0, 4 4, 0 1, 1 n n Two features: x 1, x 2 D(x 1)={c 1, n 1} D(x 2)={c 2, n 2} x 1 depends on x 2 q q n x 2=c 2: n 1 > c 1 x 2=n 2: n 1 > c 1 x 2 depends on x 1 q q X 1=c 1: n 2 > c 2 X 1=n 1: n 2 > c 2

Example: reduced CP-net n n Two features: x 1, x 2 D(x 1)={c 1, n 1} D(x 2)={c 2, n 2} x 1 depends on x 2 q q n x 2=c 2: n 1 > c 1 x 2=n 2: n 1 > c 1 x 2 depends on x 1 q q X 1=c 1: n 2 > c 2 X 1=n 1: n 2 > c 2 n n n Two features: x 1, x 2 D(x 1)={c 1, n 1} D(x 2)={c 2, n 2} x 1 and x 2 independent For x 1: n 1 > c 1 For x 2: n 2 > c 2

Example: reduced CP-net n n n Two features: x 1, x 2 D(x 1)={c 1, n 1} D(x 2)={c 2, n 2} x 1 and x 2 independent For x 1: n 1 > c 1 For x 2: n 2 > c 2 n Hard constraints: q q n x 1=n 1 x 2=n 2 Thus x 1=n 1, x 2=n 2 unique optimal solution of the CP-net and Nash equilibrium of the game

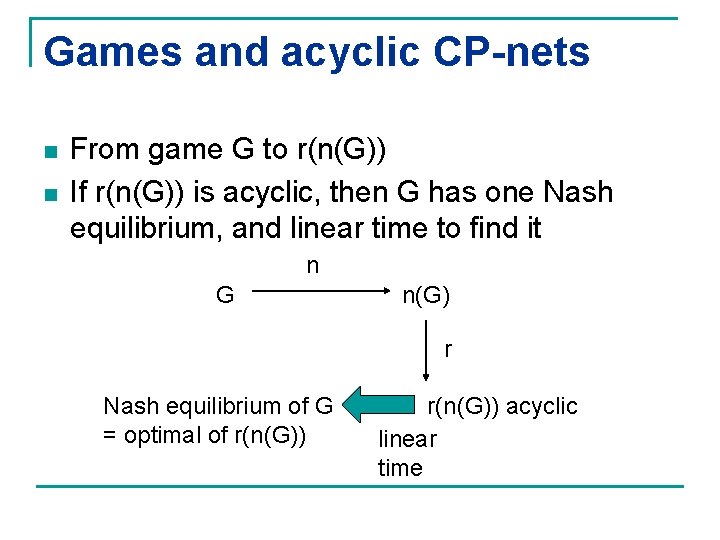
Games and acyclic CP-nets n n From game G to r(n(G)) If r(n(G)) is acyclic, then G has one Nash equilibrium, and linear time to find it n G n(G) r Nash equilibrium of G = optimal of r(n(G)) acyclic linear time

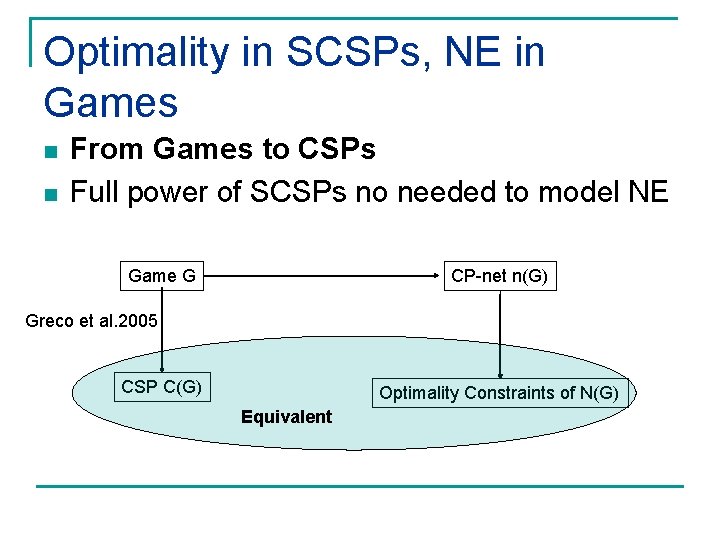
Optimality in SCSPs, NE in Games n n From Games to CSPs Full power of SCSPs no needed to model NE Game G CP-net n(G) Greco et al. 2005 CSP C(G) Optimality Constraints of N(G) Equivalent

Optimality in SCSPs, NE in Games n n From a SCSP P to a game L(P) Local Approach q q q Players: one for each variable Strategies for a player i: all values in domain of xi Payoff of player i for joint strategy s: preference for assignment s in constraints involving xi

local Example 1: Fuzzy SCSP game X Y n n n Three players x, y, z Two strategies a, b Payoff functions q q For x: px(aa-)=0. 4, px(ba-)=0. 3… For y: n n n (a, a) 0. 4 (a, b) 0. 1 (b, a) 0. 3 (b, b) 0. 5 p(aaa) = min(0. 4, 0. 4) = 0. 4 p(aba) = min(0. 1, 0. 1)=0. 1. . . Two Nash equilibria: aaa and bbb Optimal solutions: only bbb (a, a) 0. 4 (a, b) 0. 3 (b, a) 0. 1 (b, b) 0. 5 Z

local Example 2: Fuzzy SCSP game X Y n n n Three players x, y, z Two strategies a, b Payoff functions q q n n n (a, a) 0. 1 (a, b) 0. 2 (b, a) 0. 1 (b, b) 0. 2 For x: px(aa-)=0. 9, px(ba-)=0. 6… For y: n n (a, a) 0. 9 (a, b) 0. 6 (b, a) 0. 6 (b, b) 0. 9 p(aaa) = min(0. 9, 0. 1) = 0. 1 p(aab) = min(0. 6, 0. 2)=0. 2. . . Two Nash equilibria: aab and bbb Optimal solutions: only aab, abb, bab, bbb Z

Strictly monotonic combination n In general, no relationship between optimal solutions of P and Nash equilibria of L(P) However, some relationship exist if combination is strictly monotonic Thm. : Soft CSP P with strictly monotonic combination Opt(P) NE(L(P))

Classical CSPs games n n n Classical constraints are combined via logical and (which is not strictly monotonic) However, if we consider consistent CSPs, the result holds Thm. : consistent CSP Sol(P) NE(L(P))

Optimality in SCSPs, NE in Games n n Given an SCSP P, build a game GL(P): Global mapping q q q n n n Players = variables Strategies = domain values Payoff for player x for strategy s: preference value for that assignment (by looking at all constraints) Note: same payoff for all players Theorem: Opt(P) NE(GL(P)) Subset relation for all classes of SCSPs

Optimality in SCSPs, PE in Games n From a game G to an SCSP L’(G): q q Variables = players (n) Domains = strategies Semiring = Cartesian product of n semirings For each variable xi, one constraint involving xi and its neighborhood n n n pref(t) = (d 1, . . . , dn), where dj = 1 j for j i, and di = F(pi(t)) F is bijection from the payoffs to preferences in a csemiring Thm. : Game G opt(L’(G)) = PE(G)

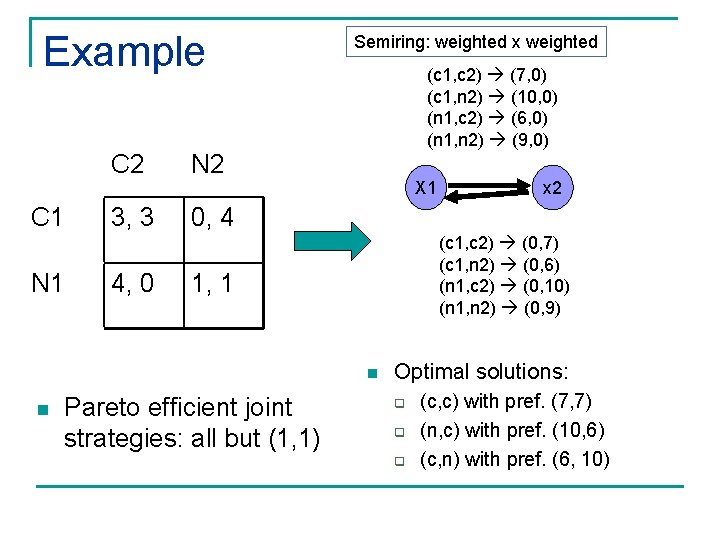
Example C 1 N 1 C 2 N 2 3, 3 0, 4 4, 0 Semiring: weighted x weighted (c 1, c 2) (7, 0) (c 1, n 2) (10, 0) (n 1, c 2) (6, 0) (n 1, n 2) (9, 0) X 1 (c 1, c 2) (0, 7) (c 1, n 2) (0, 6) (n 1, c 2) (0, 10) (n 1, n 2) (0, 9) 1, 1 n n Pareto efficient joint strategies: all but (1, 1) x 2 Optimal solutions: q q q (c, c) with pref. (7, 7) (n, c) with pref. (10, 6) (c, n) with pref. (6, 10)

Optimality in SCSPs, PE in Games n From SCSPs to Games n If we use the local mapping q n Opt(P) ⊆ PE(L(P)) If we use global mapping q Opt(P) = PE(L(P))

Summary : CP-nets and NE games 1 -1 N’ not reduced r N reduced r n(g(N)) g g g(N) n

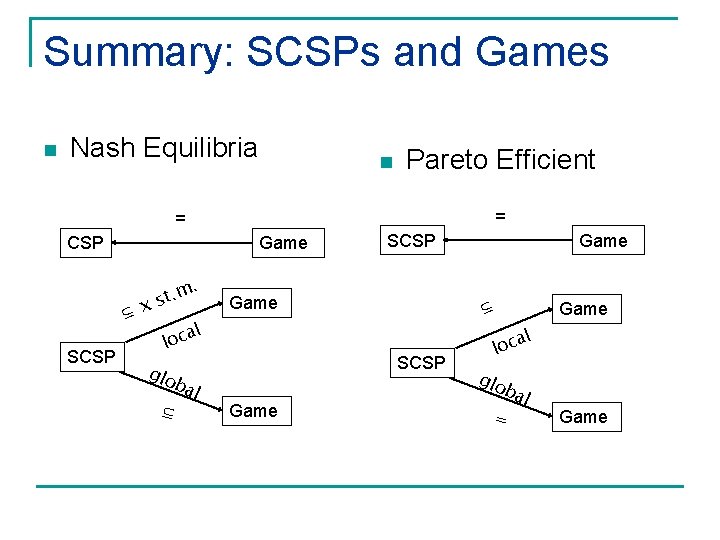
Summary: SCSPs and Games n Nash Equilibria n Pareto Efficient = = CSP Game ⊆ SCSP t. m s x . Game SCSP glo ⊆ Game ⊆ l a loc bal SCSP Game al loc glo bal = Game

References n n n CP-nets and Soft Constraints Carmel Domshlak, Steven David Prestwich, Francesca Rossi, Kristen Brent Venable, Toby Walsh: Hard and soft constraints for reasoning about qualitative conditional preferences. J. Heuristics 12(4 -5): 263 -285 (2006) C. Boutilier, R. I. Brafman, Carmel Domshlak, H. H. Hoos, and D. Poole. Preference-based constraint optimization with CP-nets. Computational Intelligence, 20(2): 137– 157, 2004 Games, CP-nets and Soft Constraints Georg Gottlob, Gianluigi Greco, Francesco Scarcello: Pure Nash Equilibria: Hard and Easy Games. J. Artif. Intell. Res. (JAIR) 24: 357 -406 (2005) Krzysztof R. Apt, Francesca Rossi, K. Brent Venable, Comparing the notions of optimality in CP-nets, strategic games, and soft constraints, to appear in Annals of Mathematics and Artificial Intelligence.