Nyquist 2 Hany Ferdinando Dept of Electrical Engineering

Nyquist (2) Hany Ferdinando Dept. of Electrical Engineering Petra Christian University Nyquist (2) - Hany Ferdinando

General Overview n n What is stability? Mapping contour The Nyquist criterion Relative Stability Nyquist (2) - Hany Ferdinando 2

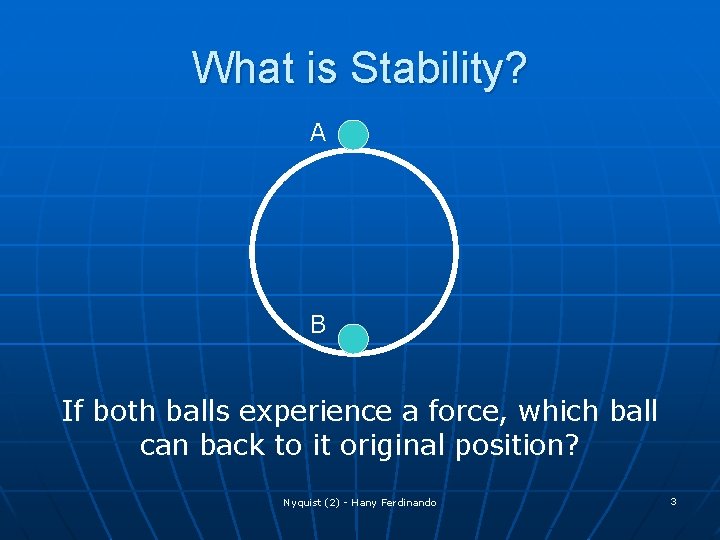
What is Stability? A B If both balls experience a force, which ball can back to it original position? Nyquist (2) - Hany Ferdinando 3

Contour A unit square contour in s-plane can be mapped into another plane via a certain function. For example, mapping a unit square contour in splane to F(s) plane by function F(s) = 2 s + 1 j A unit square contour -1 1 -j Nyquist (2) - Hany Ferdinando 4

F 1(s) = 2 s+1 s = s + jw and F(s) = u + jv, F(s) = 2(s+jw) + 1 u = 2 s + 1 and v = 2 w D j D A -1 1 C -j 2 j -1 A 3 B C s-plane -2 j B F(s)-plane Nyquist (2) - Hany Ferdinando 5

F 1(s) = 2 s+1 n n n Zero of F 1(s) = 2 s+1 is -0. 5. F 1(s) has no poles. A unit square contour in s-plane encircles zero -0. 5 once in clockwise direction. A mapping contour in F(s)-plane encircles origin once in clockwise direction. Nyquist (2) - Hany Ferdinando 6

F 2(s) = s/(s+2) D A j D A -1 1 -j C B s-plane B C F(s)-plane Nyquist (2) - Hany Ferdinando 7

F 2(s) = s/(s+2) n n n Zero of F 1(s) = s/(s+2) is 0 and its pole is -2. A unit square contour in s-plane encircles zero 0 once in clockwise direction and encircles no poles. A mapping contour in F(s)-plane encircles origin once in clockwise direction. Nyquist (2) - Hany Ferdinando 8

Chaucy’s theorem Principle of the argument: If a contour Gs in the s-plane encircles Z zeros and P poles of F(s) and does not pass through any poles and zeros of F(s) and the traversal is in the clockwise direction along the contour, the corresponding contour GF in the F(s)plane encircles the origin of the F(s)plane N = Z – P times in the clockwise direction Nyquist (2) - Hany Ferdinando 9

Chaucy’s Theorem fz 1 s fp 2 Gs fp 1 f. F GF fz 2 Nyquist (2) - Hany Ferdinando 10

Chaucy’s Theorem § The net angle for fp 1, fp 2 and fz 2 as s traverses along Gs is zero, but fz 1 is 2 p. n If there are Z zeros are enclosed by Gs in clockwise direction, then the net angle for zeros is 2 p. Z. n If there are P poles are enclosed by Gs in clockwise direction, then the net angle for poles is 2 p. P. Nyquist (2) - Hany Ferdinando 11

Chaucy’s Theorem n n n The net resultant angle of F(s), f. F, is 2 p. Z-2 p. P. f. F = 2 p. Z – 2 p. P, or 2 p. N = 2 p. Z – 2 p. P, or N=Z–P If N > 0, GF is in clockwise direction, Otherwise, is in counter clockwise. Nyquist (2) - Hany Ferdinando 12

Chaucy’s Theorem Consequences Gs Z = 3, P = 1 N=Z–P=2 Nyquist (2) - Hany Ferdinando 13

The Nyquist Criterion It starts from the characteristic equation n n A system is stable if all zeros of F(s) are in the left-hand s-plane Gs is the entire right-hand s-plane, it encloses the entire right-hand splane, then determine if there are zeros of F(s) lie within Gs Nyquist (2) - Hany Ferdinando 14

The Nyquist Criterion Now, how to map F(s) = 1 + L(s)? n n Usually, L(s) is in factored from but 1+L(s) is not Instead of mapping to F(s)-plane we can do it for L(s)-plane Nyquist (2) - Hany Ferdinando 15

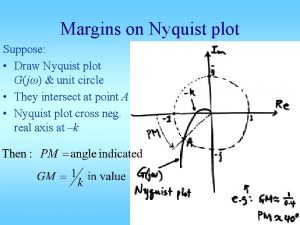
F(s)- into L(s)-plane? n n In F(s)-plane N is the number of clockwise encirclements of the origin In L(s)-plane N is the number of clockwise encirclements of the -1 point in F(s), because F’(s)=F(s)-1 Nyquist (2) - Hany Ferdinando 16

Stability Analysis n N=0 n n n N<0 n n n The system is stable if there is no pole of L(s) in the right-half plane Otherwise, the system is unstable The system is stable if the number of counter clockwise encirclement is equal to the number of poles of L(s) in the right-half plane Otherwise, the system in unstable N>0 n In this case, the system is unstable Nyquist (2) - Hany Ferdinando 17

Example (1) S-plane L(s)-plane Nyquist (2) - Hany Ferdinando 18

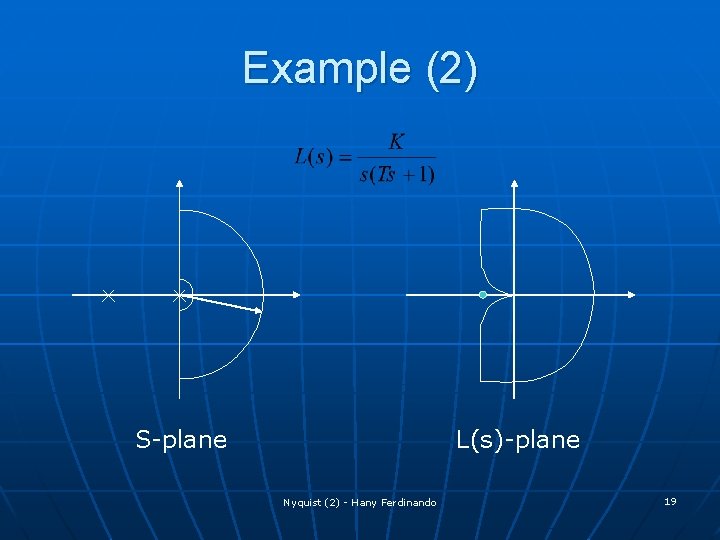
Example (2) S-plane L(s)-plane Nyquist (2) - Hany Ferdinando 19

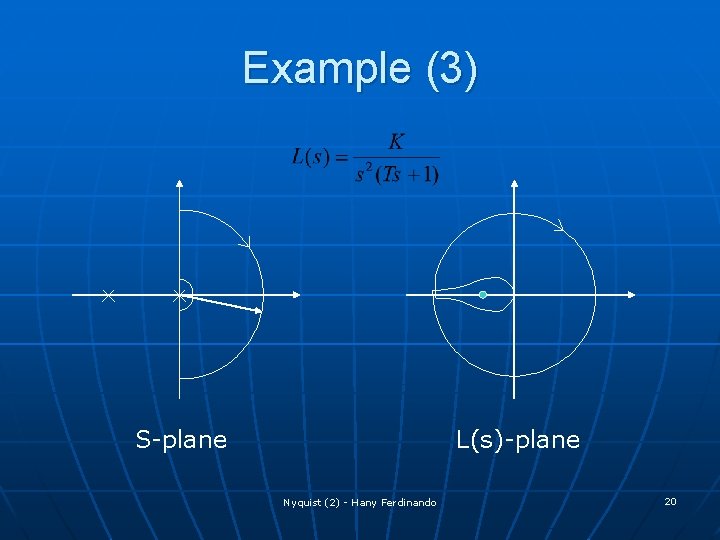
Example (3) S-plane L(s)-plane Nyquist (2) - Hany Ferdinando 20