Neuroprosthetics Week 4 Neuron Modelling Implants excite neurons

















- Slides: 20

Neuroprosthetics Week 4 Neuron Modelling

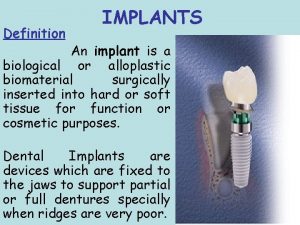
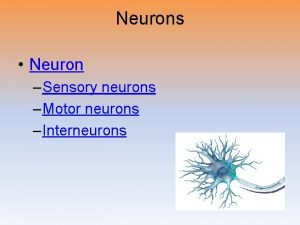
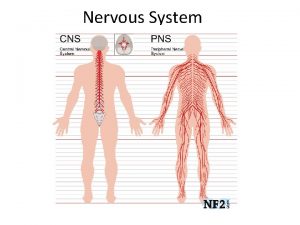
Implants excite neurons n n Retina – ganglion or bipolar cells Cochlea/Ear – spiral ganglion cells Motor prostheses – nerve-muscle junction In each example – interface between electrode and neuronal membrane

Passive properties of neuronal membrane n n n Resistance from intra and extra cellular fluids Capacitance of membrane (like a cable) Combination means spatial and temporal filtering of voltage signals Typical low pass RC circuit – losses/fidelity Spinal motor neurons or axons from retina ganglion to thalamus in brain must reliably carry signals with a frequency up to 4 KHz/1 KHz for up to 1 metre

Passive limitations n n n Rise and fall of signals given by: V(t) = V(0)exp(-t/T) where T = RC Typical RC = 1 to 100 msec – so voltage changes are slowed Same equation for distance that a signal can be detected: V(x) = V(0)exp(-x/X) where X = length constant Typical X is a few hundred micrometers

Passive response n Voltage profile for a constant current on peripheral nerve of KW

Active Membranes n n n Active membranes overcome temporal and spatial degradations Ionic gradients exist between the inside and outside of cells Exchanges between sodium, calcium and potassium – ions driven in and out of cells Action potential – brief, transient, regenerating depolarization Resting potential typically -70 m. V. External stimulus brings membrane to threshold. Cell fires or not, peak amplitude may reach +40 m. V

Ion channels n n n “Whole cell” currents represent the ensemble of thousands of individual channels Thousands of individual ion channels are responsible for membrane conductance changes Channels are selective for different types of ions

Gating n n Time dependence of the opening and closing of a channel Probability of finding a channel in an open or closed state – as a function of: membrane potential the presence of a drug or neurotransmitter

Permeation n Conductive properties of a channel in terms of its selectivity for specific ions The rate at which ions can pass through the channel (hence max current) Effects of blocking drugs

Permeation n Conductive properties of a channel in terms of its selectivity for specific ions The rate at which ions can pass through the channel (hence max current) Effects of blocking drugs

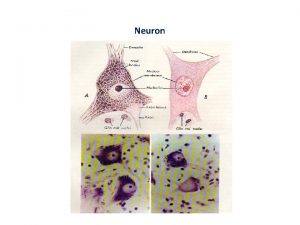
Nerve Tissue

Membrane voltage n n n The main equation for stimulation of the Soma is always: I(st) = I(io) + C d. V/dt One part of the current loads the cell membrane capacity and the other part passes through the ion channels Alternatively: d. V/dt = [ I(st) – I(io) ]/C A positive stimulating current causes V to increase To generate a spike this current must cause V to reach its threshold value

Threshold n n n Once threshold voltage is reached many of the (sodium) ion channels open The voltage increases to an action potential without the need for further stimulation Once threshold is reached the stimulus can be switched off Alternatively, once threshold is reached increasing the stimulating current further has little/no effect But different cells have different threshold values – depends on size of axons and somas

Axon models n n n Operation of axons have been modelled extensively for e. g. squid, frogs, rabbits and rats An expression for human nerve fibres is given by: d. V/dt = [ -I(Na)-I(K)-I(L)+I(st) ]/C Where I(L) is a leakage current Each current is then defined by means of a complex minimum (first) order equation

Temperature effects n n n Usually membrane model data is gathered at low temperatures Raising the temperature generally causes a shortening of the action potential and an increase in spike propagation velocity For temperatures higher than 31 to 33 deg. C action potentials no longer propagate in squid axons In warm blooded animals spike durations shorten considerably – but no heat block Threshold levels change – warmer means easier to excite!


Compartment models n n n Pieces of neuron can be treated as elements A whole neuron is represented by an electrical network Currents injected then can be treated with Kirchoffs law Resistances become internal resistances of neighbouring compartments Modeller must decide about degree of complexity Much research in this area!

Model variability n n n n Large variability in neuron models due partly to the large variability in neurons Example: absolute threshold current at the soma for a point source stimulation was: Passive model 32. 9 micro. A Hodgkin-Huxley model 43 micro. A FCM(5 ion channels) model 71 micro. A Compare with our studies (human)80 to 100 micro. A Passive (based on RC) – HH (based on squids)

Problems n n n Selective stimulation of neural tissue is an enormous challenge Example: in bladder control – activation of the detrusor muscle without activation of the urethal sphincter Every type of neuron exhibits different operating characteristics – big problem in modelling/simulation Neural geometry is complex, leading to complex models which require a high computational effort even for simple studies External stimulation/monitoring very limited

 Biotolerant implants
Biotolerant implants Kontracepcijas implants
Kontracepcijas implants Occipital nerve stimulation
Occipital nerve stimulation Imz dental implants
Imz dental implants Pros and cons of cochlear implants quizlet
Pros and cons of cochlear implants quizlet Transosteal implant
Transosteal implant Ict implants
Ict implants Ailing and failing implant
Ailing and failing implant Mitracip
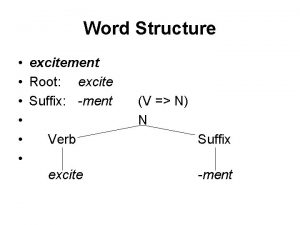
Mitracip Suffixes of excite
Suffixes of excite Calm comparative
Calm comparative Excite motore di ricerca
Excite motore di ricerca Week by week plans for documenting children's development
Week by week plans for documenting children's development Pruning neurons
Pruning neurons Everything psychological is simultaneously biological
Everything psychological is simultaneously biological Figure 8-2 neurons and neuroglia
Figure 8-2 neurons and neuroglia What are neurons composed of
What are neurons composed of Mirroring 260
Mirroring 260 Brain homunculus
Brain homunculus What is the minimum number of neurons in a reflex arc
What is the minimum number of neurons in a reflex arc Unipolar neurons are found in
Unipolar neurons are found in