Multipath Routing for Congestion Minimization Multiroute Flows Chandra

Multipath Routing for Congestion Minimization & Multiroute Flows Chandra Chekuri Univ of Illinois, Urbana. Champaign Joint work with Mark Idleman

s-t flows in directed graphs •

Flow Decomposition • Edge flow f of value v can be decomposed into a path flow in O(nm) time • A path flow of value v induces an edge flow of same value

Multi-route flows �� (st) = { p | p is a st path } �� (st, h) = {p = (p 1, p 2, . . . , ph) | each pj ∈ �� (st) and the paths are edge-disjoint } h-route s-t flow f : �� (st, h) → R+ f(p) flow on path-tuple p

s p q t

Multiroute flows: basic theorem [Kishimoto, Aggarwal-Orlin] Theorem: An acyclic edge s-t flow x : E → R+ with value v can be decomposed into a h-route flow iff x(e) ≤ v/h for all edges e 3 s 1 2 t 1 s 1 t 1

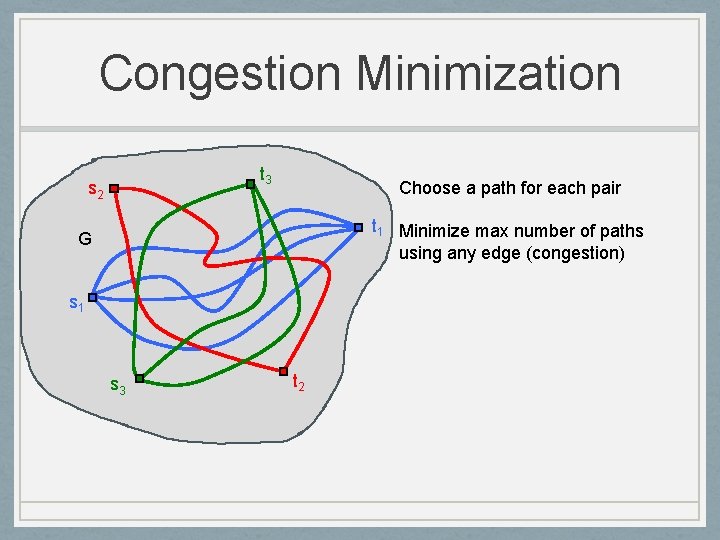
Congestion Minimization t 3 s 2 Choose a path for each pair t 1 Minimize max number of paths using any edge (congestion) G s 1 s 3 t 2

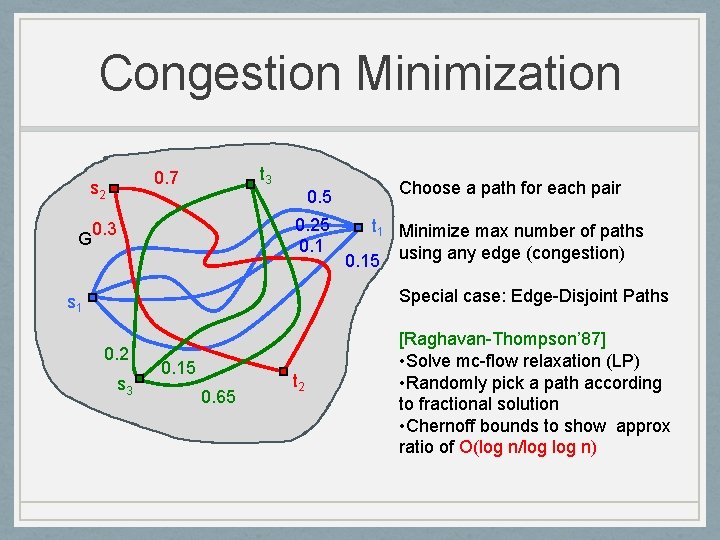
Congestion Minimization s 2 G t 3 0. 7 0. 5 0. 25 0. 1 0. 3 Choose a path for each pair t 1 Minimize max number of paths 0. 15 using any edge (congestion) Special case: Edge-Disjoint Paths s 1 0. 2 s 3 0. 15 0. 65 t 2 [Raghavan-Thompson’ 87] • Solve mc-flow relaxation (LP) • Randomly pick a path according to fractional solution • Chernoff bounds to show approx ratio of O(log n/log n)

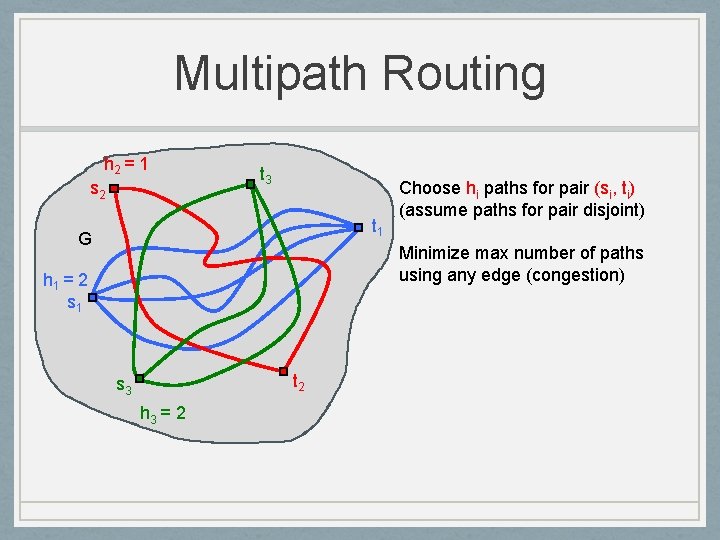
Multipath Routing h 2 = 1 s 2 t 3 t 1 G Choose hi paths for pair (si, ti) (assume paths for pair disjoint) Minimize max number of paths using any edge (congestion) h 1 = 2 s 1 t 2 s 3 h 3 = 2

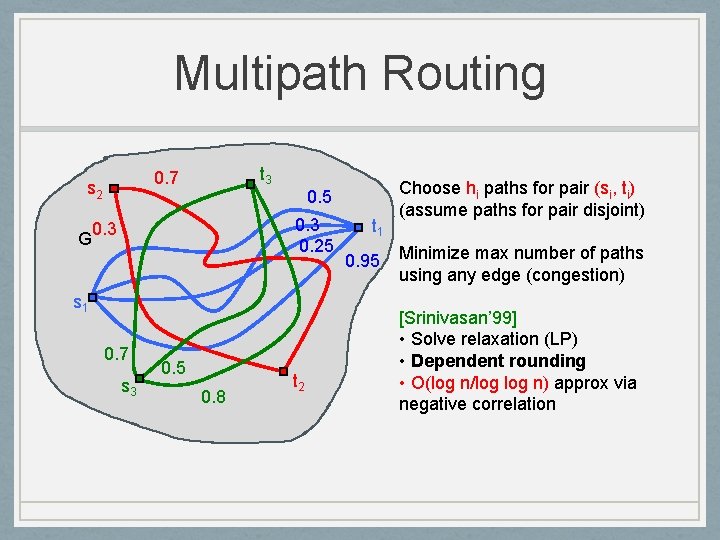
Multipath Routing s 2 G t 3 0. 7 0. 5 0. 3 0. 25 0. 3 s 1 0. 7 s 3 0. 5 0. 8 t 2 t 1 0. 95 Choose hi paths for pair (si, ti) (assume paths for pair disjoint) Minimize max number of paths using any edge (congestion) [Srinivasan’ 99] • Solve relaxation (LP) • Dependent rounding • O(log n/log n) approx via negative correlation

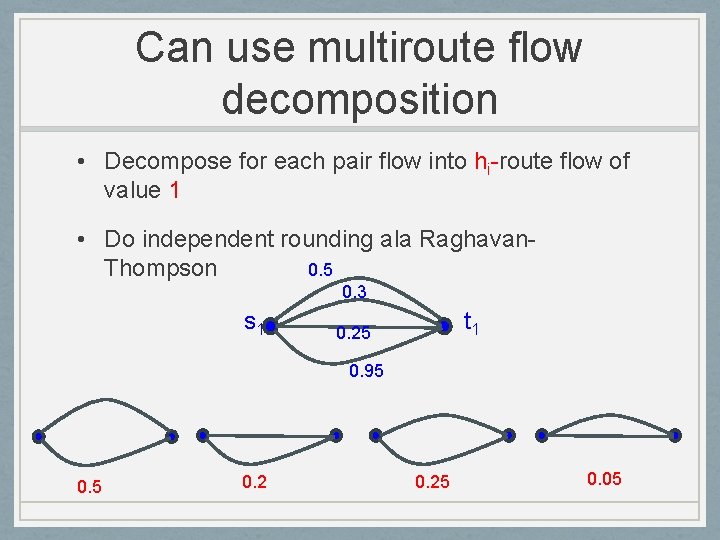
Can use multiroute flow decomposition • Decompose for each pair flow into hi-route flow of value 1 • Do independent rounding ala Raghavan. Thompson 0. 5 0. 3 s 1 t 1 0. 25 0. 95 0. 25 0. 05

Advantages • Rounding and analysis exactly the same as it is for standard congestion minimization. No need for technicalities of dependent rounding. • If paths are short can use Lovasz-Local-Lemma to reduce congestion to O(log d/log d) where d is max # of edges in any path collection of decomposition (via existing results of [Srinivasan, Moser-Tardos, Haeupler-Saha-Srinivasan])

Choosing Paths • G=(V, E) , (s 1, t 1), …, (sk, tk) and need hi edgedisjoint paths per pair • Minimize congestion

Multi-route flow LP Min C p ∈ P(siti, h) f(p) ≥ 1 for all (si, ti) p ∈ P(siti, h) : e ∈ p f(p) ≤ C f(p) ≥ 0 for all p for all e, i

Multi-route flow LP Min C p ∈ P(siti, hi) f(p) ≥ 1 for all (si, ti) p ∈ P(siti, hi) : e ∈ p f(p) ≤ C f(p) ≥ 0 for all e, i for all p How do we solve LP? 1. Ellipsoid for dual: separation oracle is min-cost flow 2. Compact LP followed by multi-route flow decomposition

Compact LP Min C for each i flow of value hi from si to ti f(e, i) ≤ 1 for all e, i ∑i f(e, i) ≤ C for all e f(e, i) ≥ 0 for all e, i Can decompose f(e, i) into multi-route hi-route-flow and choose one “path collection” for each (si, ti) independently

Compact LP Min C for each i flow of value hi from si to ti f(e, i) ≤ 1 for all e, i ∑i f(e, i) ≤ C for all e f(e, i) ≥ 0 for all e, i [Doerr-Kunnemann-Wahlstrom’ 10] solve same LP but do “standard” flow decomposition which does not guarantee disjoint paths. They employ dependent rounding after standard flow decomposition.

Choosing Short Paths • G=(V, E) , (s 1, t 1), …, (sk, tk) and need hi edgedisjoint paths per pair • Want paths for each pair to be “short”: no more than d edges in total • Minimize congestion

Min C for each i flow of value hi from si to ti f(e, i) ≤ 1 for all e, i ∑i f(e, i) ≤ C for all e f(e, i) ≥ 0 for all e, I ∑e f(e, i) ≤ d for all i • Decompose f(e, i) into multi-route hi-route-flow. • Apply filtering to find flow of value at least ½ on paths which use at most 2 d edges • Choose one “path collection” for each (si, ti) independently from short path collections • Congestion of O(log d/log d) via LLL

Concluding Remarks • Multiroute flows are useful to know • Several explicit and implicit applications in routing and network design – see refs in paper

Thank You!