Modeling the Intermittent Dynamics of Alfvn Waves in













- Slides: 25

Modeling the Intermittent Dynamics of Alfvén Waves in the Solar Wind Abraham C. -L. Chian National Institute for Space Research (INPE), Brazil & Yohsuke Kamide (Nagoya U. , Japan), Erico L. Rempel (ITA, Brazil), Wanderson M. Santana (INPE, Brazil)

Outline • Relevance of intermittency and chaos in the solar-terrestrial environment • Modeling the interplanetary Alfvén intermittency driven by chaos Ref: Chian et al. , On the chaotic nature of solar-terrestrial environment: interplanetary Alfvén intermittency, JGR 2006

Intermittency • Time series displays random regime switching between laminar and bursty periods of fluctuations • Probability distribution function (PDF) displays a non. Gaussian shape due to an excess of large- and smallamplitude fluctuations at small scales • Power spectrum displays a power-law behavior

Evidence of intermittency in the solar-terrestrial environment • Alfvén intermittency in the solar wind Bruno et al. , ASR (2005) Bruno & Carbone, http: //solarphysics. livingreviews. org (2005) • Intermittency in the Auroral Electrojet (AE) index Consolini & De Michelis, GRL (1998, 2005) • Intermittency in the earth´s plasma sheet related to bursty bulk flows in the magnetotail Angelopoulos, Mukai & Kokubun, PP (1999); Voros et al. , JGR (2004)

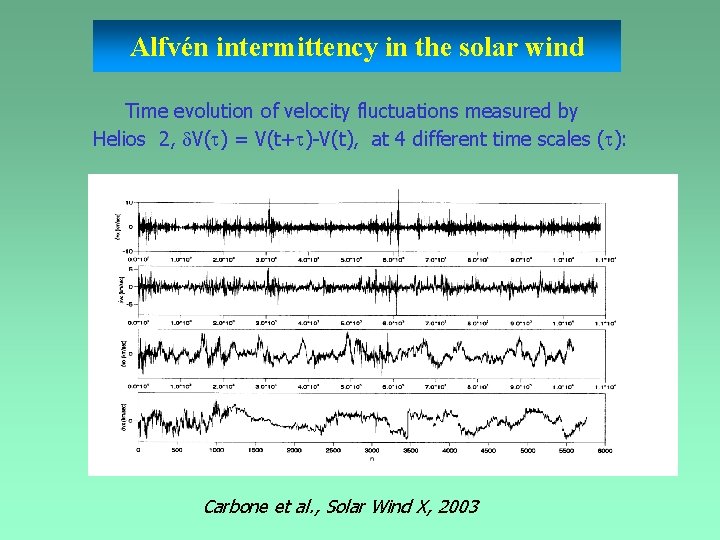
Alfvén intermittency in the solar wind Time evolution of velocity fluctuations measured by Helios 2, V( ) = V(t+ )-V(t), at 4 different time scales ( ): Carbone et al. , Solar Wind X, 2003

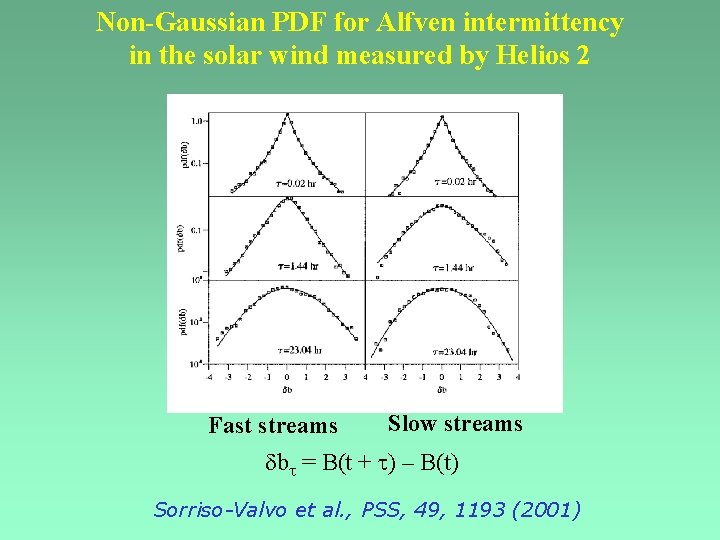
Non-Gaussian PDF for Alfven intermittency in the solar wind measured by Helios 2 Fast streams Slow streams b = B(t + ) – B(t) Sorriso-Valvo et al. , PSS, 49, 1193 (2001)

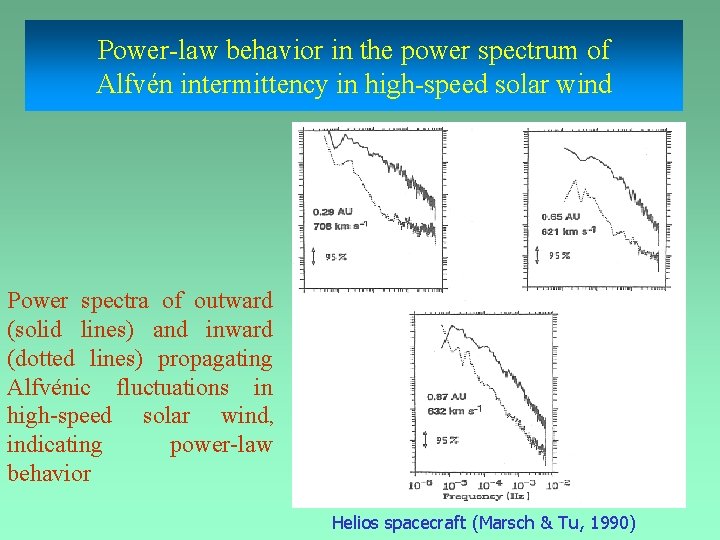
Power-law behavior in the power spectrum of Alfvén intermittency in high-speed solar wind Power spectra of outward (solid lines) and inward (dotted lines) propagating Alfvénic fluctuations in high-speed solar wind, indicating power-law behavior Helios spacecraft (Marsch & Tu, 1990)

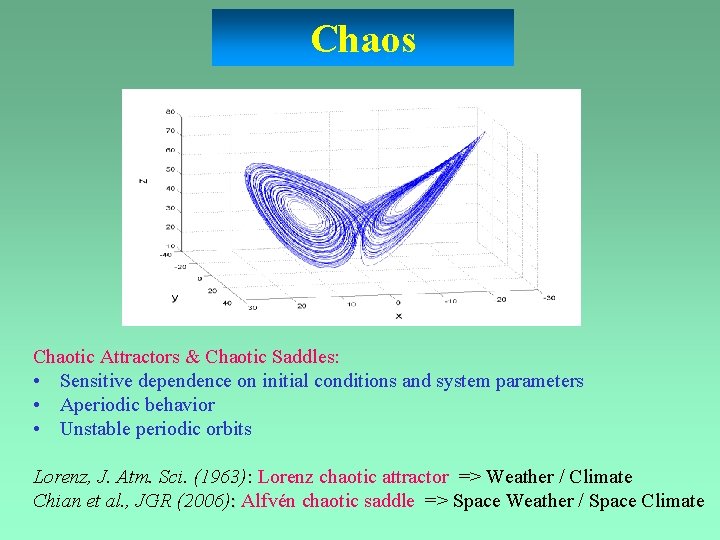
Chaos Chaotic Attractors & Chaotic Saddles: • Sensitive dependence on initial conditions and system parameters • Aperiodic behavior • Unstable periodic orbits Lorenz, J. Atm. Sci. (1963): Lorenz chaotic attractor => Weather / Climate Chian et al. , JGR (2006): Alfvén chaotic saddle => Space Weather / Space Climate

Chaotic sets • Chaotic Attractors: - Set of unstable periodic orbits Positive maximum Lyapunov exponent Attract all initial conditions in a given neighbourhood Basin of attraction (continuous stable manifolds, without gaps) Responsible for asymptotic chaos • Chaotic Saddles: - Set of unstable periodic orbits - Positive maximum Lyapunov exponent - Repel most initial conditions from their neighbourhood, except those on stable manifolds - No basin of attraction (fractal stable manifolds, with gaps) - Responsible for transient chaos

Evidence of chaos in the solar-terrestrial environment • Chaos in Alfvén turbulence in the solar wind Macek & Radaelli, PSS (2001) Macek et al. , PRE (2005) • Chaos in solar radio emissions Kurths & Karlicky, SP (1989) Kurths & Schwarz, SSRv (1994) • Chaos in the (AE, AL) auroral indices Baker et al. , GRL (1990) Sharma et al. , GRL (1993) Pavlos et al. , NPG (1999)

Derivative nonlinear Schrodinger equation Large-amplitude Alfvén wave propagating along the ambient magnetic field in the x direction: b = by+ibz h = dissipation a = 1/[4(1 - )], = c 2 S / c 2 A, = dispersion S(b, x, t) = Aexp(ik ): a circularly-polarized driver wave = x - Vt

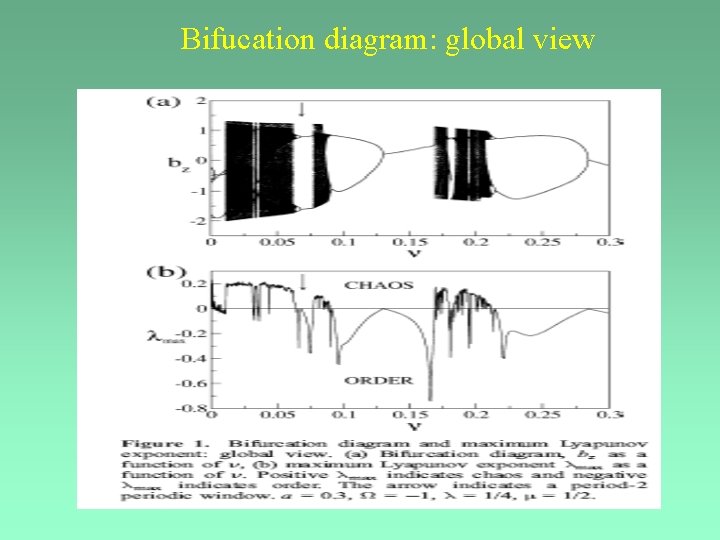
Bifucation diagram: global view

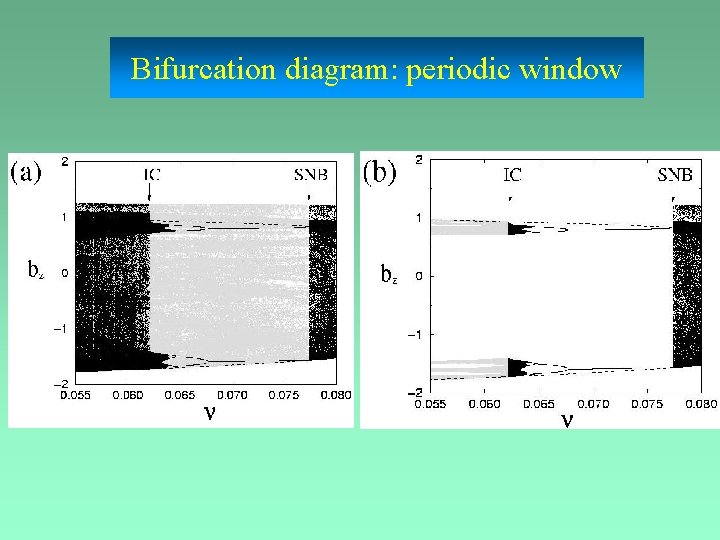
Bifurcation diagram: periodic window

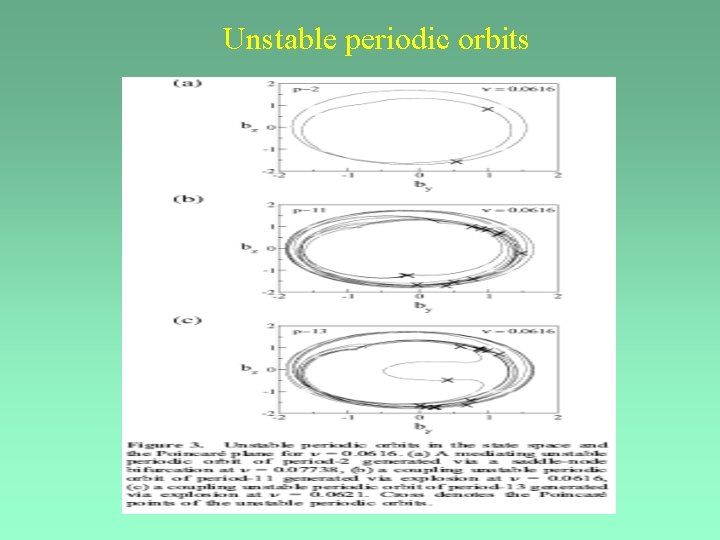
Unstable periodic orbits

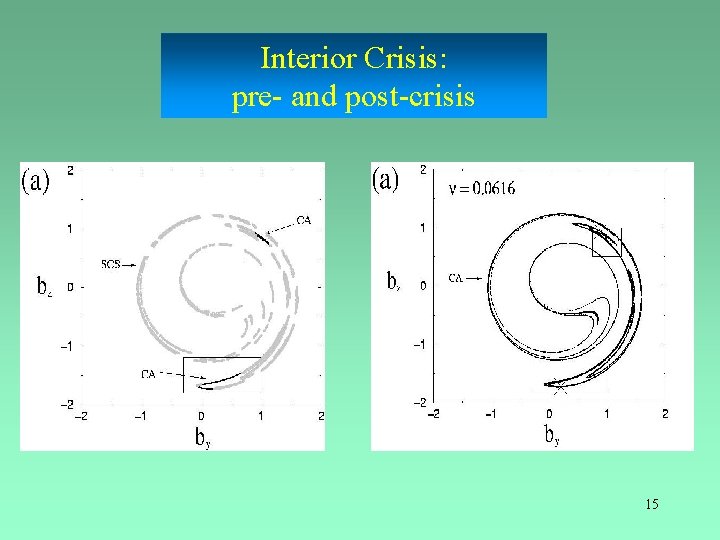
Interior Crisis: pre- and post-crisis 15

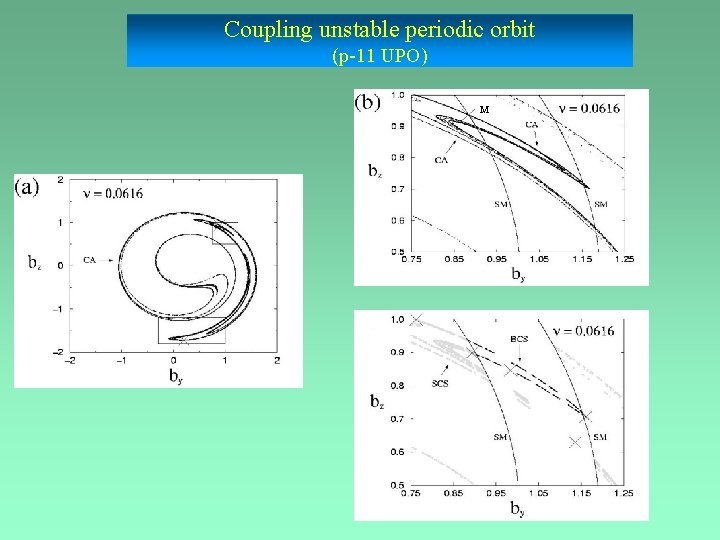
Coupling unstable periodic orbit (p-11 UPO) M

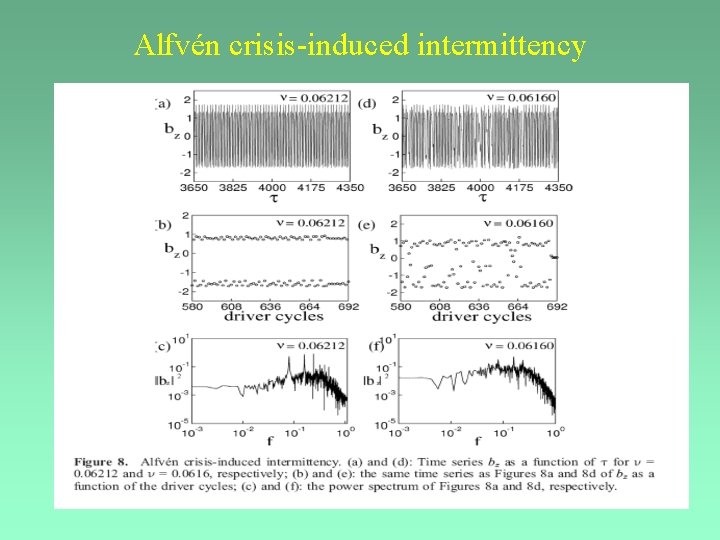
Alfvén crisis-induced intermittency

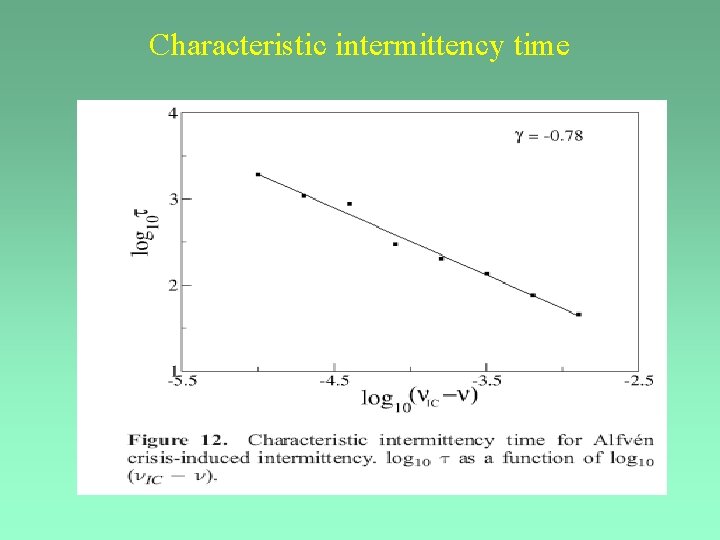
Characteristic intermittency time

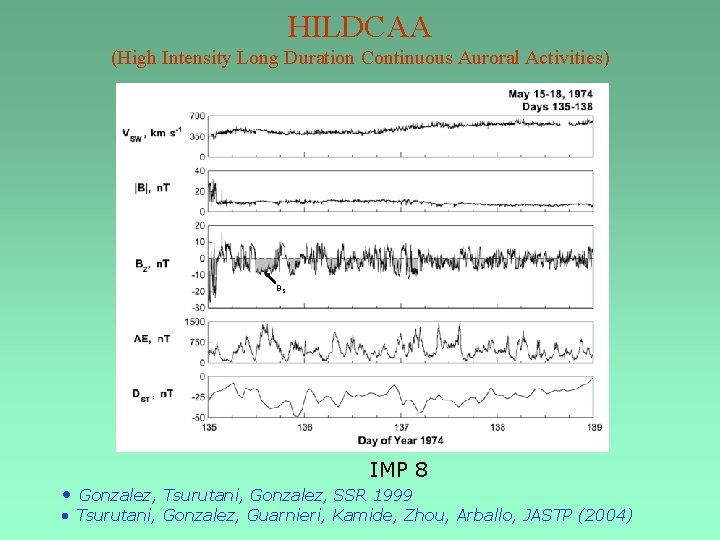
HILDCAA (High Intensity Long Duration Continuous Auroral Activities) BS • IMP 8 Gonzalez, Tsurutani, Gonzalez, SSR 1999 • Tsurutani, Gonzalez, Guarnieri, Kamide, Zhou, Arballo, JASTP (2004)

CONCLUSIONS • Observational evidence of chaos and intermittency in the Sun-Earth system • Dynamical systems approach provides a powerfull tool to probe the complex nature of solar-terrestrial environment, e. g. , Alfvén intermittent turbulence in the solar wind • Unstable structures (unstable periodic orbits and chaotic saddles) are the origin of intermittent turbulence • Characteristic intermittency time can be useful for space weather and space climate forecasting

Books • Handbook of Solar-Terrestrial Environment Y. Kamide and A. C. -L. Chian (Eds. ) Springer, 2006 (ASSE 2006) • Fundamentals of Space Environment Science V. Jatenco, A. C. -L Chian, J. F. Valdes and M. A. Shea (Eds. ) Elsevier, 2005 (ASSE 2004) • Advances in Space Environment Research A. C. -L. Chian and the WISER Team (Eds. ) Kluwer, 2003 (WSEF 2002, HPC 2002) • Complex Systems Approach to Economic Dynamics A. C. -L. Chian Springer, 2006 WISER mission: ‘linking nations for the peaceful use of the earth-ocean-space environment’ (www. cea. inpe. br/wiser)

THANK YOU !

Two approaches to dynamical systems • Low-dimensional chaos: Stationary solutions of the derivative nonlinear Schroedinger equation Hada et al. , Phys. Fluids 1990 Chian et al. , Ap. J 1998 Borotto et al. , Physica D 2004 Rempel et al. , Phys. Plasmas 2006 Chian et al. , JGR 2006 • High-dimensional chaos: Spatiotemporal solutions of the Kuramoto-Sivashinsky equation and the regularized long-wave equation Chian et al. , Phys. Rev. E 2002 He and Chian, Phys. Rev. Lett. 2003 He and Chian, Phy. Rev. E 2004 Rempel and Chian, Phys. Rev. E 2005

Unstable periodic orbits & turbulence • UPOS in the Kuramoto-Sivashinsky equation Christiansen et al. , Nonlinearity 1997; Zoldi and Greenside, PRE 1998 • Identification of an UPO in plasma turbulence in a tokamak experiment Bak et al, PRL 1999 • Sensitivity of chaotic attractor of a barotropic ocean model to external influences can be described by UPOs Kazantsev, NPG, 2001 • Intermittency of a shell model of fluid turbulence is described by an UPO Kato and Yamada, Phys. Rev. 2003 • Control of chaos in a fluid turbulence by stabilization of an UPO Kawahara and Kida, J. Fluid Mech. 2001; Kawahara, Phys. Fluids 2005

Chaotic saddles & turbulence • Supertransient in the complex Ginzburg-Landau equation Braun and Feudel, PRE 1996 • Detecting and computing chaotic sadddles in higher dimensions Sweet, Nusse and Yorke, PRL 1996 • Close to the transition from laminar to turbulent flows the turbulent state corresponds to a chaotic saddle Eckhardt and Mersmann, PRE 1999 • Chemical and biological activity in open flows Tél et al, Phys. Rep. 2005 • Dispersion of finite-size particles in open chaotic advection Vilela, de Moura and Grebogi, PRE 2006 • Edge of chaos in a parallel shear flow Skufca, Yorke and Eckhardt, PRL 2006
 Dimensional modeling vs relational modeling
Dimensional modeling vs relational modeling Helen c. erickson
Helen c. erickson What is a semiconductor used for
What is a semiconductor used for Surface waves and body waves
Surface waves and body waves Difference between electromagnetic waves and sound waves
Difference between electromagnetic waves and sound waves Mechanical waves and electromagnetic waves similarities
Mechanical waves and electromagnetic waves similarities Example of mechanical wave
Example of mechanical wave Is a seismic wave mechanical or electromagnetic
Is a seismic wave mechanical or electromagnetic Characteristics of a longitudinal wave
Characteristics of a longitudinal wave Mechanical vs electromagnetic waves
Mechanical vs electromagnetic waves Light is an electromagnetic wave true or false
Light is an electromagnetic wave true or false Mechanical waves and electromagnetic waves
Mechanical waves and electromagnetic waves Compare and contrast p waves and s waves using venn diagram
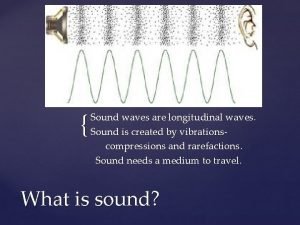
Compare and contrast p waves and s waves using venn diagram Sound is a longitudinal wave
Sound is a longitudinal wave Similarities of mechanical and electromagnetic waves
Similarities of mechanical and electromagnetic waves Mechanical waves characteristics
Mechanical waves characteristics Constructive waves and destructive waves difference
Constructive waves and destructive waves difference Intermittent explosive disorder
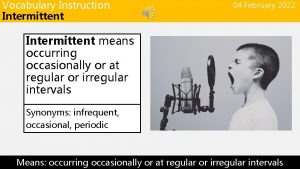
Intermittent explosive disorder Chain intermittent symbol
Chain intermittent symbol Intermittent reinforcement
Intermittent reinforcement Explosive disorder
Explosive disorder Intermittent kmc
Intermittent kmc Learning definition psychology
Learning definition psychology Laser weld symbol
Laser weld symbol Va loan intermittent occupancy
Va loan intermittent occupancy Synchronized intermittent mandatory ventilation
Synchronized intermittent mandatory ventilation