mildly Large clique is hard on average for

(mildly) Large clique is hard on average for resolution Shuo Pang Jan. 2020 BIRS

v v lower bound lbd for an intermediate model

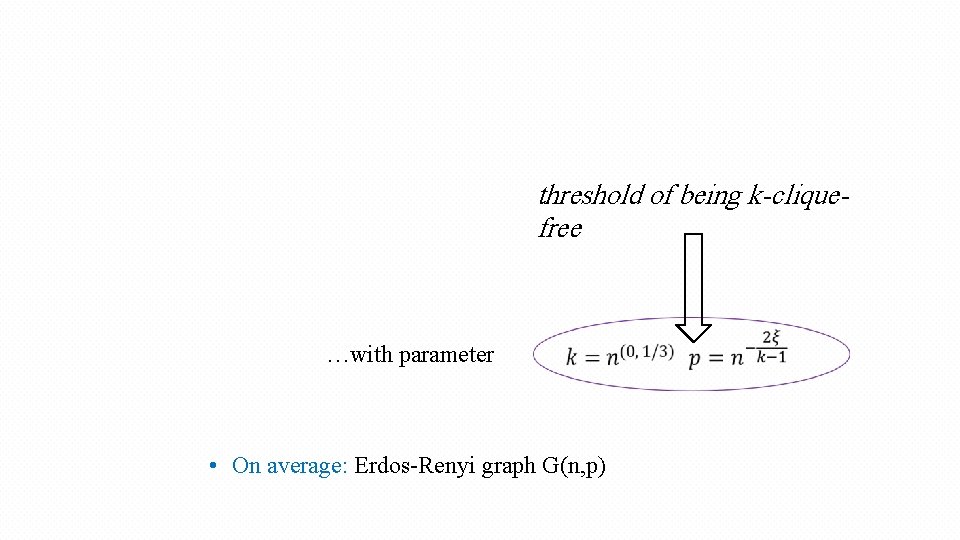
k-Clique Given n-vertex graph G, is there a k(n)-clique in it? • Average case – random graphs G(n, p) Robust; hopefully gives clue about algorithmic hardness Proof complexity form Is k-clique hard on average for system P? • On average: Erdos-Renyi graph G(n, p)

threshold of being k-cliquefree …with parameter • On average: Erdos-Renyi graph G(n, p)

o Our target: Resolution [BIS 07]: [BGL 13]: [ABd. RLNR 18]: (the real large) for tree-like for regular resolution o Encoding: block ver. Captures ``internal’’ hardness (from G)

First result Theorem [P 19] For , any holds for resolution. , w. h. p. the -size lower bound

Proof sketch General strategy To show many clauses must appear Define a class of clauses that each one is `small’, while together `complete’ (Here, intuitively: clause that almost already reveals a partial-clique assignment say of size 0. 01 k. ) Definition. (Narrowness) Pigeon is narrow in R: vertices R allows to go is non (r, q)-neighbor-dense (r=0. 01 k). Definition. (Usefulness) A clause containing > 0. 01 k narrow or settled pigeons.

Ø Bottleneck counting (cf. [Pudlak 00]) • Start with a random r/2 -clique , (An r/2 -subset of [k] at random; choose each place from comm. neighb. of previous) • Branch till some useful R appears. Claim I. One can always lead the process to some useful clause. (completeness) Claim II. Probability to each such clause is small. (smallness)

Summary o o The strategy is classic; Relatively simple pseudorandom properties.

Next goal: towards o The strategy is classic; …perhaps the same strategy, but finer pseudorandom properties. (``mostly-denseness’’) Theorem. [ABd. R+18] W. h. p. G is mostly-dense. For such G, -lbd on regular resolution holds.

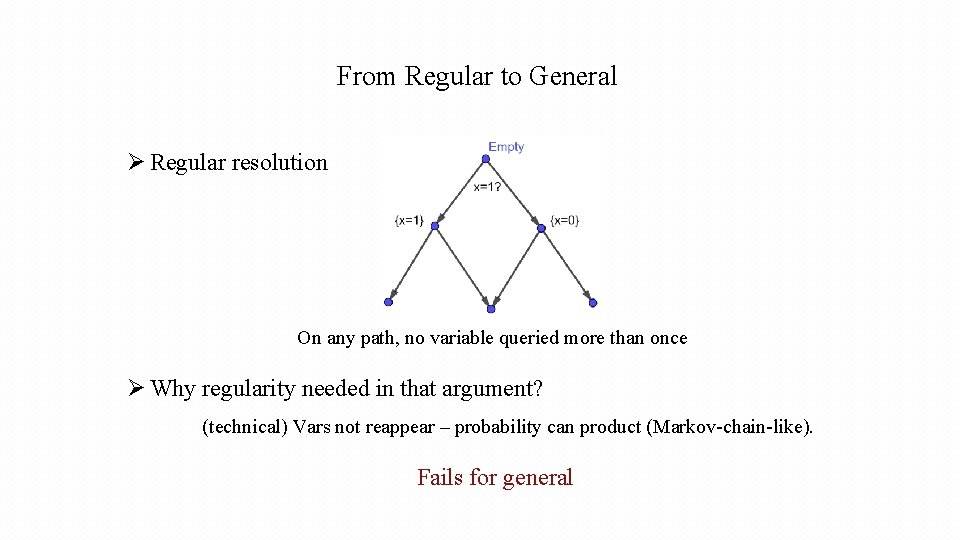
From Regular to General Ø Regular resolution On any path, no variable queried more than once Ø Why regularity needed in that argument? (technical) Vars not reappear – probability can product (Markov-chain-like). Fails for general

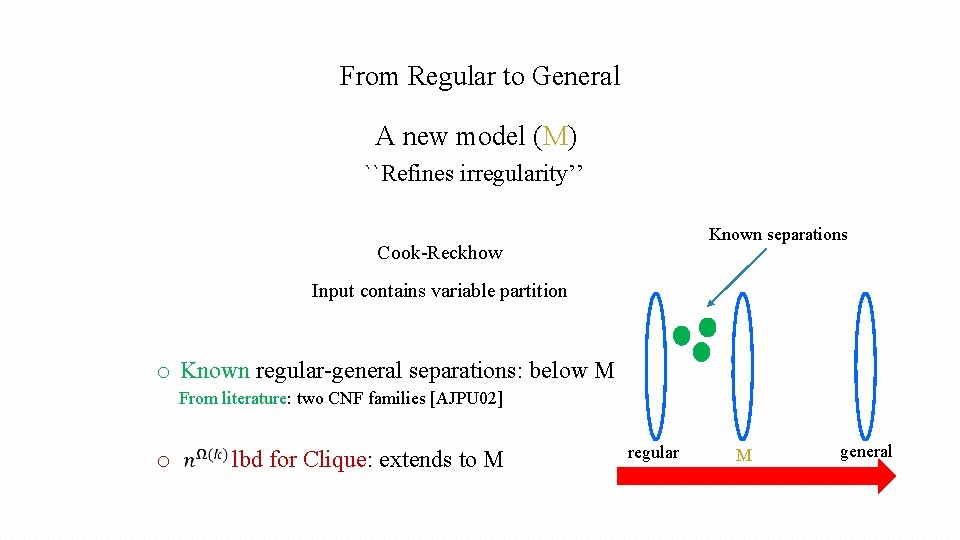
From Regular to General A new model (M) ``Refines irregularity’’ Known separations Cook-Reckhow Input contains variable partition o Known regular-general separations: below M From literature: two CNF families [AJPU 02] o lbd for Clique: extends to M regular M general

The model (a-irregular resolution) [P 19] Input: CNF & a partition of variables If a clause C touches > a-potion blocks (``block-width’’): Under C proof is regular, except on a-portion blocks (of vars). Ø Known separations: (naturally) fit in. Known power of general-over-regular is actually M-over-regular. almost- (Even for extremely small a)

Second result Theorem [P 19] On G(n, p) with the natural k-block-partition of variables, w. h. p. requires size for any -irregular resolution. constant

Proof sketch Ø Idea Regular result + self-reduction Useful C exists (as before) Find restriction (Proof simpler) consistent with C s. t. regular under C (using usefulness) (Instance remains hard) still quasi-random Apply regular result. Subtlety: key quasi-randomness likely not inherited. Fix: in short, relativize it.

Open problems v Weak lbd for PC v Regarding ``block-partitioned’’ model, is there possibile block-width vs size relation? (under reasonable restrictions)

Thank you